SOCS : un acronyme utile pour décrire les distributions

En statistiques, nous souhaitons souvent comprendre comment un ensemble de données est distribué. En particulier, il y a quatre choses qu’il est utile de savoir sur une distribution :

1 . Forme

• La distribution est-elle symétrique ou biaisée d’un côté ?
• La distribution est-elle unimodale (un pic) ou bimodale (deux pics) ?

2. Valeurs aberrantes

• Y a-t-il des valeurs aberrantes présentes dans la distribution ?

3. Centre

• Quelle est la moyenne, la médiane et le mode de distribution ?

4. Propagation

• Q uels sont l’étendue, l’étendue interquartile, l’écart type et la variance de la distribution ?

SOCS est un acronyme utile que nous pouvons utiliser pour mémoriser ces quatre choses. Cela signifie « forme, valeurs aberrantes, centre, propagation ».

Passons en revue un exemple simple de la façon d’utiliser SOCS pour décrire une distribution.

Exemple : Comment utiliser SOCS pour décrire une distribution

Supposons que nous disposions de l’ensemble de données suivant qui montre la hauteur d’un échantillon de 20 plantes différentes.

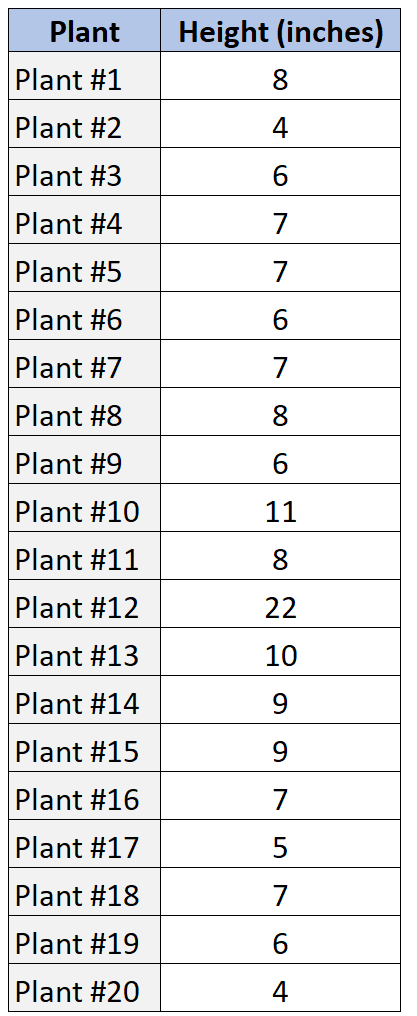
Voici comment nous pouvons utiliser SOCS pour décrire cette distribution de valeurs de données.

Forme

Tout d’abord, nous voulons décrire la forme de la distribution.

Un moyen utile de visualiser la forme de la distribution consiste à créer un histogramme, qui affiche les fréquences de chaque valeur de l’ensemble de données :

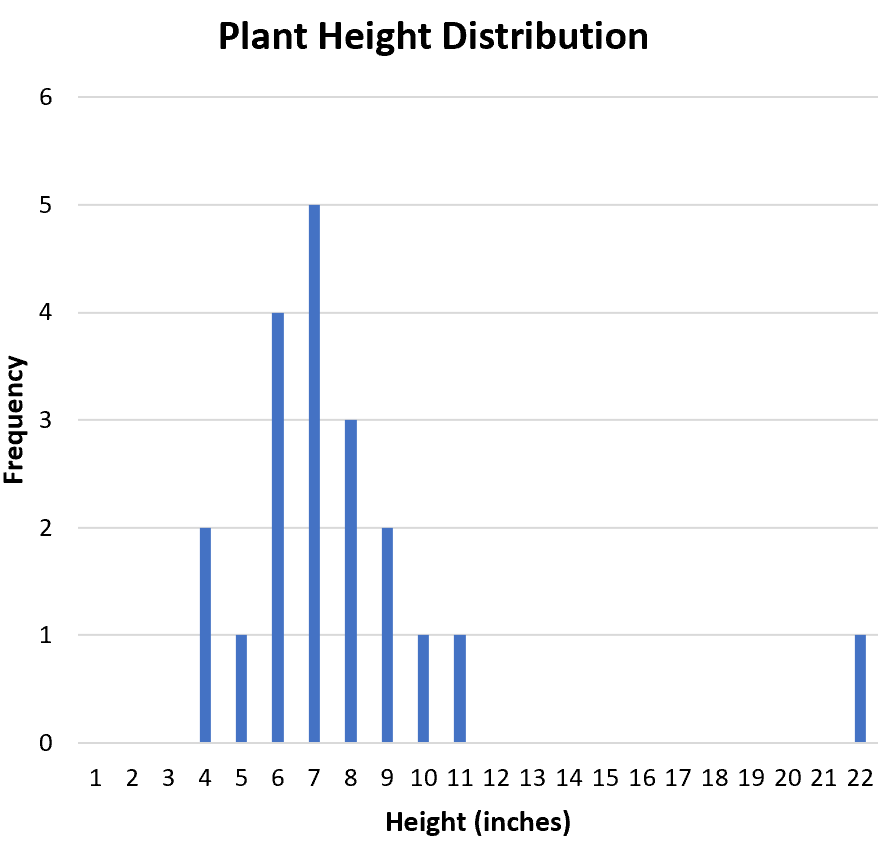
La distribution est-elle symétrique ou biaisée d’un côté ?   D’après l’histogramme, nous pouvons voir que la distribution est à peu près symétrique. Autrement dit, les valeurs ne sont pas biaisées d’un côté ou de l’autre.

La distribution est-elle unimodale (un pic) ou bimodale (deux pics) ? La distribution est unimodale. Il a un pic à la valeur « 7 ».

Valeurs aberrantes

Ensuite, nous voulons déterminer s’il existe des valeurs aberrantes dans l’ensemble de données. À partir de l’histogramme, nous pouvons inspecter visuellement la distribution et voir que 22 est potentiellement une valeur aberrante :

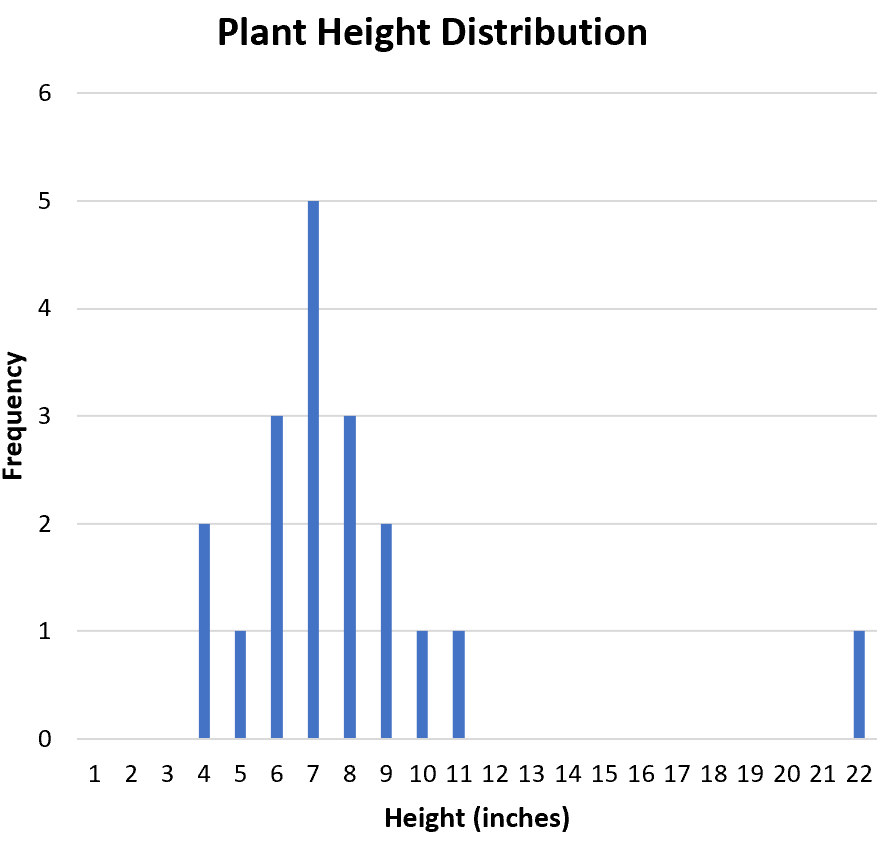
Une façon courante de définir formellement une valeur aberrante est toute valeur qui est 1,5 fois l’intervalle interquartile au-dessus du troisième quartile ou en dessous du premier quartile.

À l’aide du calculateur d’intervalle interquartile , nous pouvons saisir les 20 valeurs de données brutes et constater que le troisième quartile est 9 , l’intervalle interquartile est 3 , et donc toute valeur supérieure à 9 + (1,5*3) = 13,5 est une valeur aberrante, par définition.

Puisque 22 est supérieur à 13,5, nous pouvons déclarer que 22 est une valeur aberrante.

Centre

Nous souhaitons ensuite décrire où se situe le centre de la distribution. Trois mesures courantes de tendance centrale que nous pouvons utiliser sont la moyenne, la médiane et le mode.

Moyenne : Il s’agit de la valeur moyenne de la distribution. Nous trouvons cela en additionnant toutes les valeurs individuelles, puis en divisant par le nombre total de valeurs :

Moyenne = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Médiane : Il s’agit de la valeur « moyenne » de la distribution. Nous trouvons cela en classant toutes les valeurs de la plus petite à la plus grande, puis en identifiant la valeur médiane. Il s’avère que c’est 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7 , 7, 7 , 7, 8, 8, 8, 9, 9, 10, 11, 22

Mode : Il s’agit de la valeur qui apparaît le plus fréquemment. Il s’avère que c’est 7 .

Propagé

Ensuite, nous souhaitons décrire la répartition des valeurs dans la distribution. Quatre mesures courantes de dispersion que nous pouvons utiliser sont l’intervalle, l’intervalle interquarile, l’écart type et la variance.

Plage : il s’agit de la différence entre la valeur la plus grande et la plus petite de l’ensemble de données. Cela s’avère être 22 – 4 = 18 .

Plage interquartile : mesure la largeur des 50 % centraux des valeurs de données. En saisissant les 20 valeurs de données brutes dans le calculateur d’intervalle interquartile , nous pouvons voir que cela est égal à 3 .

Écart type : il s’agit d’une mesure de la répartition moyenne des valeurs des données. En saisissant les 20 valeurs de données brutes dans le calculateur de variance et d’écart type, nous pouvons voir que l’écart type est égal à 3,69 .

Variance : Il s’agit simplement de l’écart type, au carré. Ceci est égal à 3,69 ² = 13,63 .

Conclusion

En utilisant SOCS comme guide, nous avons pu décrire la répartition des hauteurs des plantes de la manière suivante :

• La distribution était unimodale et symétrique, ce qui signifie qu’elle n’avait qu’un seul pic et qu’elle n’était pas asymétrique d’un côté ou de l’autre.
• La distribution avait une valeur aberrante : 22.
• La distribution avait une moyenne de 7,85, une médiane de 7 et un mode de 7.
• La distribution avait un intervalle de 18, un intervalle interquartile de 3, un écart type de 3,69 et une variance de 13,63.

Notez que nous pouvons utiliser SOCS pour décrire n’importe quelle distribution, ce qui est un moyen utile pour nous de bien comprendre la forme d’une distribution, si elle présente des valeurs aberrantes, où se trouve approximativement le centre et comment répartir les valeurs des données. sont.