L’aplatissement peut-il être négatif ?

En statistiques, l’aplatissement est utilisé pour décrire la forme d’une distribution de probabilité.

Plus précisément, cela nous indique dans quelle mesure les valeurs des données se regroupent dans les queues ou au sommet d’une distribution.

L’aplatissement d’une distribution peut être négatif, égal à zéro ou positif.

Zéro Kurtosis

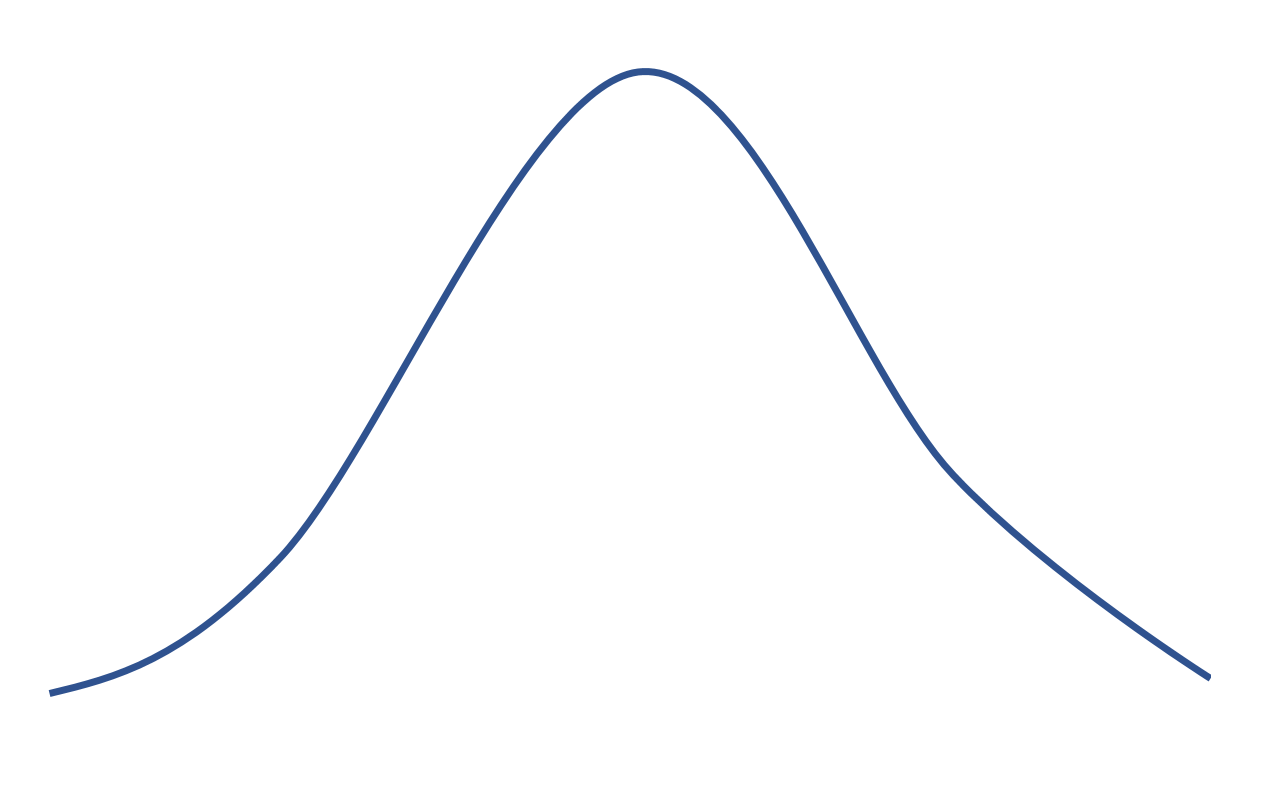
Si une distribution a un aplatissement de 0, alors elle est égale à la distribution normale qui a la forme de cloche suivante :

Aplatissement positif

Si une distribution a un aplatissement positif, elle est dite leptokurtique , ce qui signifie qu’elle a un pic plus net et des queues plus lourdes par rapport à une distribution normale.

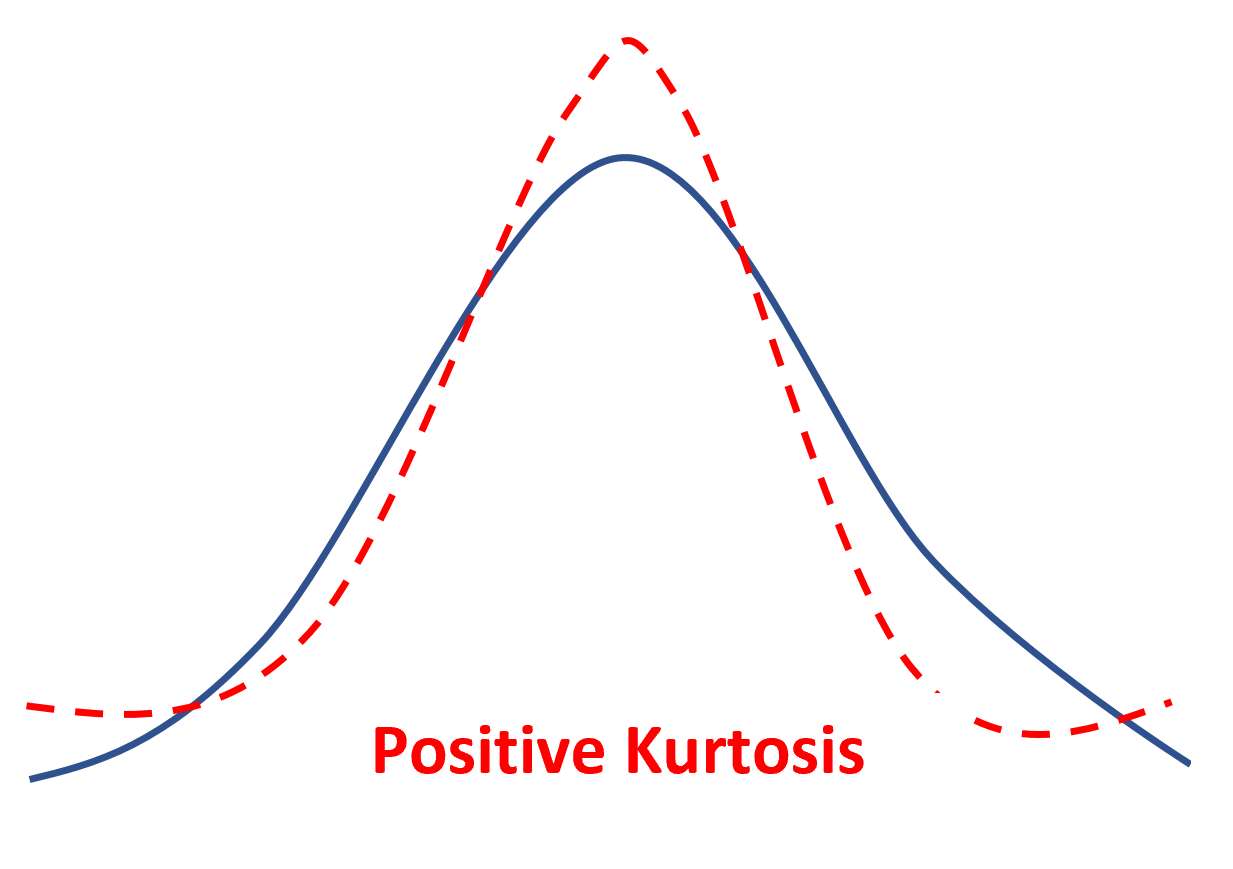
Cela signifie simplement que moins de valeurs de données sont situées près de la moyenne et plus de valeurs de données sont situées sur les queues.

La distribution la plus connue qui a un aplatissement positif est la distribution t, qui a un pic plus net et des queues plus lourdes par rapport à la distribution normale.

Aplatissement négatif

Si une distribution a un aplatissement négatif, elle est dite platykurtique , ce qui signifie qu’elle a un pic plus plat et des queues plus fines par rapport à une distribution normale.

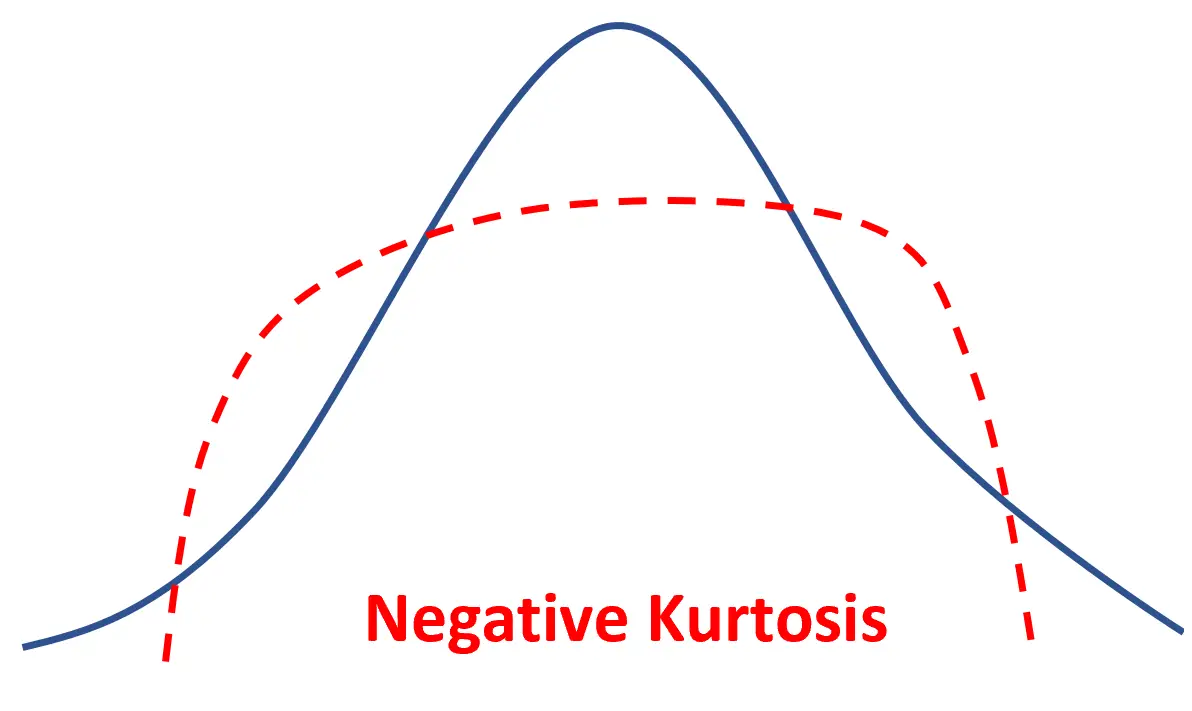
Cela signifie simplement que davantage de valeurs de données sont situées près de la moyenne et moins de valeurs de données sont situées sur les queues.

Un exemple extrême de distribution présentant un aplatissement négatif est la distribution uniforme , qui n’a aucun pic et est une distribution complètement plate.

Quand utiliser l’aplatissement en pratique

En pratique, nous mesurons souvent l’ aplatissement d’une distribution dans la phase exploratoire de l’analyse lorsque nous essayons simplement de mieux comprendre les données.

Ainsi, si nous constatons que l’aplatissement est positif, nous savons que nous travaillons avec une distribution qui a moins de valeurs de données situées près du centre et davantage de valeurs de données réparties le long des queues.

À l’inverse, si nous constatons que l’aplatissement est négatif, nous savons que nous travaillons avec une distribution qui a plus de valeurs de données situées près du centre et moins de valeurs de données dans les queues.

Ressources additionnelles

Pour trouver l’asymétrie et l’aplatissement d’une distribution donnée, vous pouvez saisir les valeurs des données brutes dans ce calculateur d’asymétrie et d’aplatissement , qui vous indiquera à la fois l’asymétrie et l’aplatissement de la distribution.

L’un des tests statistiques les plus populaires utilisés pour déterminer si une distribution particulière présente ou non une asymétrie et un aplatissement qui correspondent à une distribution normale est le test de Jarque Bera .

Khan Academy propose également une belle série de vidéos qui décrivent comment classer les formes de distributions.