Comment calculer l’intervalle interquartile (IQR) dans Excel

Ce didacticiel explique comment calculer l’ intervalle interquartile d’un ensemble de données dans Excel.

Qu’est-ce que l’intervalle interquartile ?

L’ intervalle interquartile , souvent appelé IQR, est un moyen de mesurer la répartition des 50 % centraux d’un ensemble de données. Il est calculé comme la différence entre le premier quartile* (Q1) et le troisième quartile (Q3) d’un ensemble de données.

*Les quartiles sont simplement des valeurs qui divisent un ensemble de données en quatre parties égales.

Par exemple, supposons que nous ayons l’ensemble de données suivant :

[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]

Le troisième quartile s’avère être 91 et le premier quartile est 75,5 . Ainsi, l’intervalle interquartile (IQR) pour cet ensemble de données est de 91 – 75,5 = 15 . Cela nous indique la répartition des 50 % centraux des valeurs dans cet ensemble de données.

Comment calculer l’intervalle interquartile dans Excel

Microsoft Excel n’a pas de fonction intégrée pour calculer l’IQR d’un ensemble de données, mais nous pouvons facilement le trouver en utilisant la fonction QUARTILE() , qui prend les arguments suivants :

QUARTILE(tableau, quart)

• array : le tableau de données qui vous intéresse.
• quart : le quartile que vous souhaitez calculer.

Exemple : recherche d’IQR dans Excel

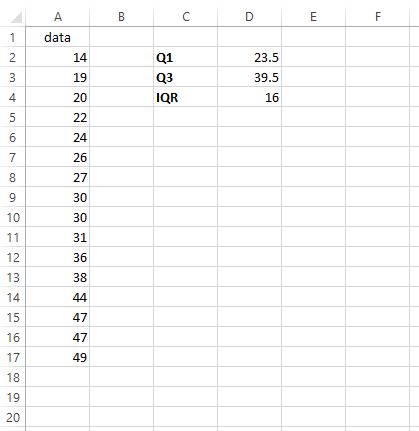
Supposons que nous souhaitions trouver l’IQR pour l’ensemble de données suivant :

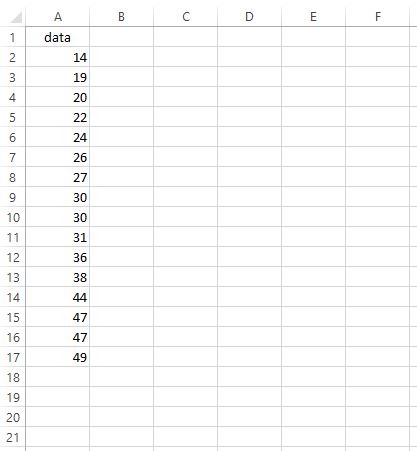
Pour trouver l’IQR, nous pouvons effectuer les étapes suivantes :

Étape 1 : Recherchez Q1 .

Pour trouver le premier quartile, nous tapons simplement =QUARTILE(A2:A17, 1) dans n’importe quelle cellule de notre choix :

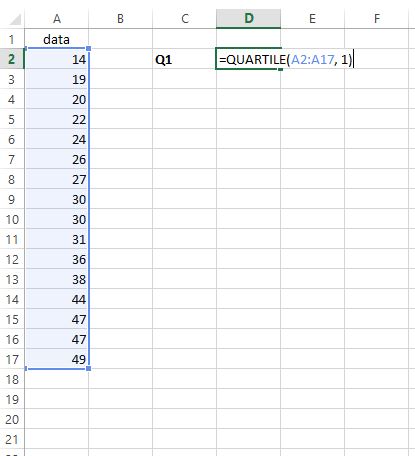
Étape 2 : Recherchez Q3 .

Pour trouver le troisième quartile, nous tapons =QUARTILE(A2:A17, 3) dans n’importe quelle cellule de notre choix :

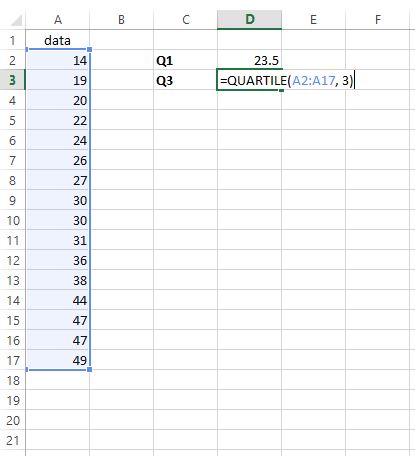
Étape 3 : Trouvez IQR .

Pour trouver l’intervalle interquartile (IQR), nous soustrayons simplement Q1 de Q3 :

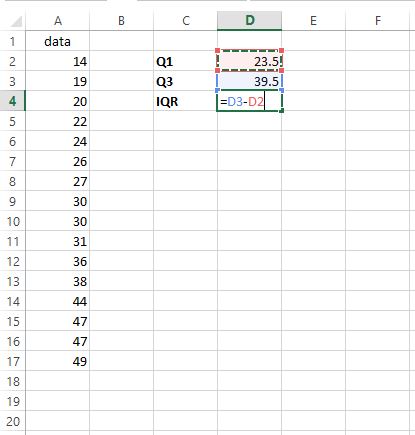
L’IQR s’avère être de 39,5 – 23,5 = 16 . Cela nous indique à quel point les 50 % centraux des valeurs sont répartis dans cet ensemble de données particulier.

Une approche plus courte

Notez que nous aurions également pu trouver l’intervalle interquartile de l’ensemble de données dans l’exemple précédent en utilisant une formule :

=QUARTILE(A2:A17, 3) – QUARTILE(A2:A17, 1)

Cela donnerait également la valeur 16 .

Conclusion

L’intervalle interquartile ne représente qu’une façon de mesurer la « propagation » d’un ensemble de données. D’autres façons de mesurer la propagation sont la plage, l’écart type et la variance .

L’avantage de l’utilisation de l’IQR pour mesurer la propagation est qu’il résiste aux valeurs aberrantes . Puisqu’il nous indique uniquement la répartition des 50 % moyens de l’ensemble de données, il n’est pas affecté par des valeurs aberrantes inhabituellement petites ou inhabituellement grandes.

Cela en fait un moyen préférable de mesurer la dispersion par rapport à une métrique telle que la plage, qui nous indique simplement la différence entre les valeurs les plus grandes et les plus petites d’un ensemble de données.

Connexe : Comment calculer le milieu de gamme dans Excel