Statistiques descriptives ou inférentielles : quelle est la différence ?

Il existe deux branches principales dans le domaine des statistiques :

• Statistiques descriptives
• Statistiques déductives

Ce tutoriel explique la différence entre les deux branches et pourquoi chacune est utile dans certaines situations.

Statistiques descriptives

En un mot, les statistiques descriptives visent à décrire un ensemble de données brutes à l’aide de statistiques récapitulatives, de graphiques et de tableaux.

Les statistiques descriptives sont utiles car elles vous permettent de comprendre un groupe de données beaucoup plus rapidement et facilement que de simplement regarder des lignes et des lignes de valeurs de données brutes.

Par exemple, supposons que nous disposions d’un ensemble de données brutes montrant les résultats aux tests de 1 000 élèves d’une école particulière. Nous pourrions être intéressés par la note moyenne aux tests ainsi que par la répartition des résultats des tests.

À l’aide de statistiques descriptives, nous pourrions trouver le score moyen et créer un graphique qui nous aide à visualiser la répartition des scores.

Cela nous permet de comprendre les résultats des tests des étudiants beaucoup plus facilement que de simplement regarder les données brutes.

Formes courantes de statistiques descriptives

Il existe trois formes courantes de statistiques descriptives :

1. Statistiques récapitulatives. Ce sont des statistiques qui résument les données à l’aide d’un seul nombre. Il existe deux types courants de statistiques récapitulatives :

• Mesures de tendance centrale : ces nombres décrivent où se trouve le centre d’un ensemble de données. Les exemples incluent la moyenne   et la médiane .
• Mesures de dispersion : ces nombres décrivent la répartition des valeurs dans l’ensemble de données. Les exemples incluent l’ intervalle , l’intervalle interquartile , l’écart type et la variance .

2. Graphiques . Les graphiques nous aident à visualiser les données. Les types courants de graphiques utilisés pour visualiser les données comprennent les diagrammes en boîte , les histogrammes , les diagrammes à tiges et à feuilles et les nuages de points .

3. Tableaux . Les tableaux peuvent nous aider à comprendre comment les données sont distribuées. Un type courant de tableau est le tableau de fréquence , qui nous indique combien de valeurs de données se situent dans certaines plages.

Exemple d’utilisation de statistiques descriptives

L’exemple suivant illustre comment nous pourrions utiliser les statistiques descriptives dans le monde réel.

Supposons que 1 000 élèves d’une certaine école passent tous le même test. Nous souhaitons comprendre la distribution des résultats des tests, nous utilisons donc les statistiques descriptives suivantes :

1. Statistiques récapitulatives

Moyenne : 82,13 . Cela nous indique que la note moyenne au test parmi les 1 000 étudiants est de 82,13.

Médiane : 84. Cela nous indique que la moitié de tous les élèves ont obtenu un score supérieur à 84 et l’autre moitié un score inférieur à 84.

Max : 100. Min : 45. Cela nous indique que la note maximale obtenue par tout élève était de 100 et la note minimale était de 45. La plage – qui nous indique la différence entre le maximum et le minimum – est de 55.

2. Graphiques

Pour visualiser la distribution des résultats des tests, nous pouvons créer un histogramme – un type de graphique qui utilise des barres rectangulaires pour représenter les fréquences.

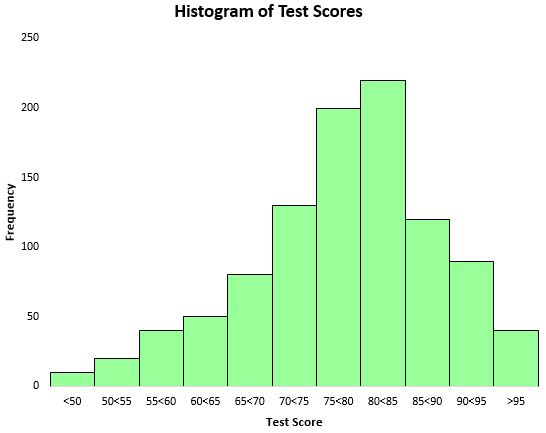
Sur la base de cet histogramme, nous pouvons voir que la distribution des résultats aux tests est à peu près en forme de cloche. La plupart des étudiants ont obtenu entre 70 et 90, tandis que très peu ont obtenu un score supérieur à 95 et encore moins un score inférieur à 50.

3. Tableaux

Un autre moyen simple de comprendre la distribution des scores consiste à créer un tableau de fréquence. Par exemple, le tableau de fréquence suivant montre le pourcentage d’élèves ayant obtenu des scores entre différentes fourchettes :

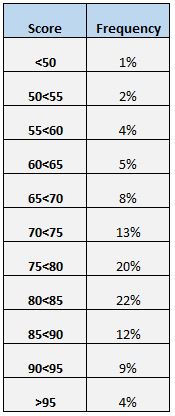
Nous pouvons voir que seulement 4 % du total des étudiants ont obtenu un score supérieur à 95. Nous pouvons également voir que (12 % + 9 % + 4 % = ) 25 % de tous les étudiants ont obtenu un score de 85 ou plus.

Un tableau de fréquence est particulièrement utile si nous voulons savoir quel pourcentage des valeurs de données se situe au-dessus ou en dessous d’une certaine valeur. Par exemple, supposons que l’école considère qu’un résultat au test « acceptable » est tout résultat supérieur à 75.

En regardant le tableau des fréquences, nous pouvons facilement voir que (20 % + 22 % + 12 % + 9 % + 4 % = ) 67 % des étudiants ont obtenu une note acceptable au test.

Statistiques déductives

En un mot, les statistiques inférentielles utilisent un petit échantillon de données pour tirer des conclusions sur la population plus large dont provient l’échantillon.

Par exemple, nous pourrions vouloir comprendre les préférences politiques de millions de personnes dans un pays.

Cependant, il serait trop long et trop coûteux d’interroger chaque individu dans le pays. Ainsi, nous prendrions plutôt une enquête plus petite auprès, disons, de 1 000 Américains, et utiliserions les résultats de l’enquête pour tirer des conclusions sur la population dans son ensemble.

C’est toute la prémisse des statistiques inférentielles : nous voulons répondre à une question sur une population, nous obtenons donc des données pour un petit échantillon de cette population et utilisons les données de l’échantillon pour tirer des inférences sur la population.

L’importance d’un échantillon représentatif

Afin d’être sûrs de notre capacité à utiliser un échantillon pour tirer des conclusions sur une population, nous devons nous assurer que nous disposons d’un échantillon représentatif , c’est-à-dire un échantillon dans lequel les caractéristiques des individus de l’échantillon correspondent étroitement aux caractéristiques de l’échantillon. de la population globale.

Idéalement, nous voulons que notre échantillon ressemble à une « mini-version » de notre population. Ainsi, si l’on veut tirer des conclusions sur une population d’élèves composée à 50 % de filles et à 50 % de garçons, notre échantillon ne serait pas représentatif s’il comprenait 90 % de garçons et seulement 10 % de filles.

Si notre échantillon n’est pas similaire à la population globale, nous ne pouvons pas généraliser avec certitude les résultats de l’échantillon à la population globale.

Comment obtenir un échantillon représentatif

Pour maximiser les chances d’obtenir un échantillon représentatif, vous devez vous concentrer sur deux choses :

1. Assurez-vous d’utiliser une méthode d’échantillonnage aléatoire.

Il existe plusieurs méthodes d’échantillonnage aléatoire que vous pouvez utiliser et qui sont susceptibles de produire un échantillon représentatif, notamment :

• Un simple échantillon aléatoire
• Un échantillon aléatoire systématique
• Un échantillon aléatoire en grappe
• Un échantillon aléatoire stratifié

Les méthodes d’échantillonnage aléatoire ont tendance à produire des échantillons représentatifs car chaque membre de la population a une chance égale d’être inclus dans l’échantillon.

2. Assurez-vous que la taille de votre échantillon est suffisamment grande .

En plus d’utiliser une méthode d’échantillonnage appropriée, il est important de s’assurer que l’échantillon est suffisamment grand pour que vous disposiez de suffisamment de données pour pouvoir généraliser à une population plus large.

Pour déterminer la taille de votre échantillon, vous devez tenir compte de la taille de la population que vous étudiez, du niveau de confiance que vous souhaitez utiliser et de la marge d’erreur que vous considérez comme acceptable.

Heureusement, vous pouvez utiliser des calculatrices en ligne pour saisir ces valeurs et voir quelle doit être la taille de votre échantillon.

Formes courantes de statistiques inférentielles

Il existe trois formes courantes de statistiques inférentielles :

1. Tests d’hypothèses.

Nous souhaitons souvent répondre à des questions sur une population telles que :

• Le pourcentage de personnes dans l’Ohio soutenant le candidat A est-il supérieur à 50 % ?
• La hauteur moyenne d’une certaine plante est-elle égale à 14 pouces ?
• Y a-t-il une différence entre la taille moyenne des élèves de l’école A et de celle de l’école B ?

Pour répondre à ces questions, nous pouvons effectuer un test d’hypothèse , qui nous permet d’utiliser les données d’un échantillon pour tirer des conclusions sur les populations.

2. Intervalles de confiance .

Parfois, nous souhaitons estimer une certaine valeur pour une population. Par exemple, nous pourrions nous intéresser à la hauteur moyenne d’une certaine espèce végétale en Australie.

Au lieu de faire le tour et de mesurer chaque plante du pays, nous pourrions collecter un petit échantillon de plantes et mesurer chacune d’entre elles. Ensuite, nous pouvons utiliser la hauteur moyenne des plantes de l’échantillon pour estimer la hauteur moyenne de la population.

Cependant, il est peu probable que notre échantillon fournisse une estimation parfaite de la population. Heureusement, nous pouvons tenir compte de cette incertitude en créant un intervalle de confiance , qui fournit une plage de valeurs dans laquelle nous sommes sûrs que le véritable paramètre de population se situe.

Par exemple, nous pourrions produire un intervalle de confiance à 95 % de [13,2, 14,8], ce qui signifie que nous sommes sûrs à 95 % que la véritable hauteur moyenne de cette espèce végétale se situe entre 13,2 pouces et 14,8 pouces.

3. Régression .

Parfois, nous souhaitons comprendre la relation entre deux variables dans une population.

Par exemple, supposons que nous voulions savoir si les heures consacrées à étudier par semaine sont liées aux résultats des tests . Pour répondre à cette question, nous pourrions effectuer une technique connue sous le nom d’analyse de régression .

Ainsi, nous pouvons observer le nombre d’heures étudiées ainsi que les résultats des tests pour 100 étudiants et effectuer une analyse de régression pour voir s’il existe une relation significative entre les deux variables.

Si la valeur p de la régression s’avère significative , alors nous pouvons conclure qu’il existe une relation significative entre ces deux variables dans la population globale des étudiants.

La différence entre les statistiques descriptives et inférentielles

En résumé, la différence entre les statistiques descriptives et inférentielles peut être décrite comme suit :

Les statistiques descriptives utilisent des statistiques récapitulatives, des graphiques et des tableaux pour décrire un ensemble de données.

Ceci est utile pour nous aider à comprendre rapidement et facilement un ensemble de données sans passer par toutes les valeurs de données individuelles.

Les statistiques inférentielles utilisent des échantillons pour tirer des conclusions sur des populations plus larges.

En fonction de la question à laquelle vous souhaitez répondre concernant une population, vous pouvez décider d’utiliser une ou plusieurs des méthodes suivantes : tests d’hypothèse, intervalles de confiance et analyse de régression.

Si vous choisissez d’utiliser l’une de ces méthodes, gardez à l’esprit que votre échantillon doit être représentatif de votre population , sinon les conclusions que vous tirerez ne seront pas fiables.