Comment lire le tableau de distribution du chi carré

Ce tutoriel explique comment lire et interpréterle tableau de distribution du Chi carré .

Qu’est-ce que le tableau de distribution du chi carré ?

Le tableau de distribution du Chi carré est un tableau qui montre les valeurs critiques de la distribution du Chi carré. Pour utiliser le tableau de distribution du Chi carré, vous n’avez besoin que de connaître deux valeurs :

• Les degrés de liberté pour le test du Chi carré
• Le niveau alpha du test (les choix courants sont 0,01, 0,05 et 0,10)

L’image suivante montre les 20 premières lignes du tableau de distribution du Chi carré, avec les degrés de liberté sur le côté gauche du tableau et les niveaux alpha en haut du tableau :

Remarque : Vous pouvez trouverici un tableau de distribution du Chi carré complet avec plus de degrés de liberté.

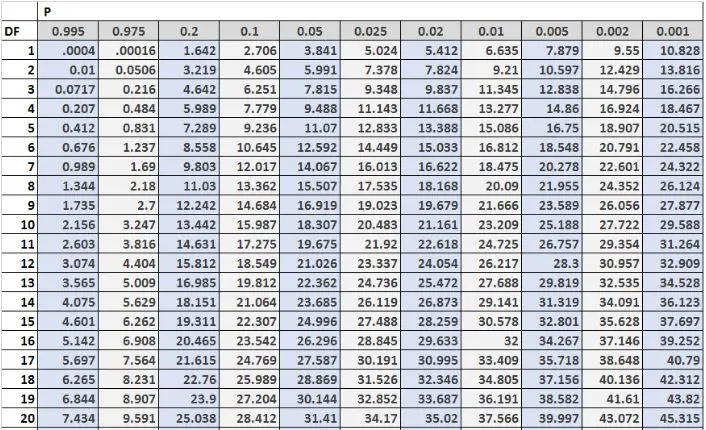
Les valeurs critiques du tableau sont souvent comparées aux statistiques de test d’un test du Chi carré. Si la statistique du test est supérieure à la valeur critique trouvée dans le tableau, vous pouvez alors rejeter l’hypothèse nulle du test du Chi carré et conclure que les résultats du test sont statistiquement significatifs.

Exemples d’utilisation du tableau de distribution du chi carré

Nous montrerons comment utiliser la table de distribution du Chi carré avec les trois types de tests du Chi carré suivants :

• Test du chi carré pour l’indépendance
• Test du chi carré pour la qualité de l’ajustement
• Test du chi carré pour l’homogénéité

Test du chi carré pour l’indépendance

Nous utilisons un test du Chi carré pour l’indépendance lorsque nous voulons tester s’il existe ou non une association significative entre deux variables catégorielles.

Exemple : Supposons que nous voulions savoir si le sexe est associé ou non à la préférence pour un parti politique. Nous prenons un échantillon aléatoire simple de 500 électeurs et les interrogeons sur leur préférence en matière de parti politique. En utilisant un niveau de signification de 0,05, nous effectuons un test du chi carré pour déterminer si le sexe est associé à la préférence pour un parti politique. Le tableau suivant présente les résultats de l’enquête :

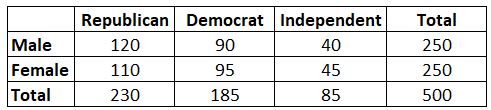
Il s’avère que la statistique de test pour ce test du Chi carré est de 0,864.

Ensuite, nous pouvons trouver la valeur critique du test dans le tableau de distribution du Chi carré. Les degrés de liberté sont égaux à (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 et le problème nous a dit que nous devions utiliser un niveau alpha de 0,05. Ainsi, selon le tableau de distribution du Chi carré, la valeur critique du test est de 5,991 .

Puisque notre statistique de test est inférieure à notre valeur critique, nous ne parvenons pas à rejeter l’hypothèse nulle. Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une association entre le sexe et les préférences en matière de parti politique.

Test du chi carré pour la qualité de l’ajustement

Nous utilisons un test d’ajustement du chi carré lorsque nous voulons tester si une variable catégorielle suit ou non une distribution hypothétique.

Exemple : un propriétaire de magasin affirme que 30 % de tous ses clients du week-end viennent le vendredi, 50 % le samedi et 20 % le dimanche. Un chercheur indépendant visite le magasin un week-end aléatoire et constate que 91 clients le vendredi, 104 le samedi et 65 le dimanche. En utilisant un niveau de signification de 0,10, nous effectuons un test du chi carré pour vérifier la qualité de l’ajustement afin de déterminer si les données sont cohérentes avec l’affirmation du propriétaire du magasin.

Dans ce cas, la statistique du test s’avère être 10,616.

Ensuite, nous pouvons trouver la valeur critique du test dans le tableau de distribution du Chi carré. Les degrés de liberté sont égaux à (#outcomes-1) = 3-1 = 2 et le problème nous dit que nous devons utiliser un niveau alpha de 0,10. Ainsi, selon le tableau de distribution du Chi carré, la valeur critique du test est de 4,605 .

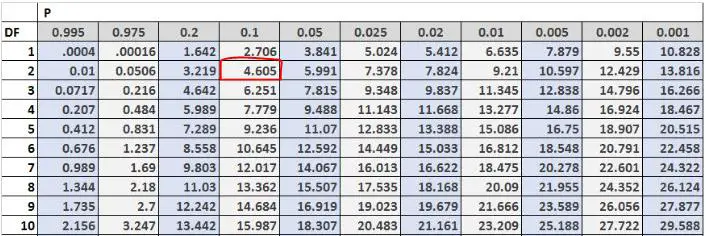
Puisque notre statistique de test est supérieure à notre valeur critique, nous rejetons l’hypothèse nulle. Cela signifie que nous disposons de suffisamment de preuves pour affirmer que la véritable répartition des clients qui viennent dans ce magasin le week-end n’est pas égale à 30 % le vendredi, 50 % le samedi et 20 % le dimanche.

Test du chi carré pour l’homogénéité

Nous utilisons un test du Chi carré pour l’homogénéité lorsque nous voulons tester formellement s’il existe ou non une différence de proportions entre plusieurs groupes.

Exemple : Un centre d’entraînement de basket-ball souhaite voir si deux nouveaux programmes d’entraînement améliorent la proportion de ses joueurs qui réussissent un test de tir difficile. 172 joueurs sont assignés au hasard au programme 1, 173 au programme 2 et 215 au programme en cours. Après avoir utilisé les programmes d’entraînement pendant un mois, les joueurs passent ensuite un test de tir. Le tableau ci-dessous indique le nombre de joueurs qui réussissent le test de tir, en fonction du programme qu’ils ont utilisé.

En utilisant un niveau de signification de 0,05, nous effectuons un test du chi carré pour déterminer si le taux de réussite est le même pour chaque programme de formation.

Il s’avère que la statistique de test pour ce test du Chi carré est de 4,208.

Ensuite, nous pouvons trouver la valeur critique du test dans le tableau de distribution du Chi carré. Les degrés de liberté sont égaux à (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 et le problème nous a dit que nous devions utiliser un niveau alpha de 0,05. Ainsi, selon le tableau de distribution du Chi carré, la valeur critique du test est de 5,991 .

Puisque notre statistique de test est inférieure à notre valeur critique, nous ne parvenons pas à rejeter l’hypothèse nulle. Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer que les trois programmes de formation produisent des résultats différents.