Comment créer un intervalle de confiance à l’aide de la distribution F

Pour déterminer si les variances de deux populations sont égales, nous pouvons calculer le rapport de variance σ ² ₁ / σ ² ₂ , où σ ² ₁ est la variance de la population 1 et σ ² ₂ est la variance de la population 2.

Pour estimer le véritable rapport de variance de la population, nous prenons généralement un échantillon aléatoire simple de chaque population et calculons le rapport de variance de l’échantillon, s ₁ ² / s ₂ ² , où s ₁ ² et s ₂ ² sont les variances de l’échantillon pour l’échantillon 1 et l’échantillon. 2, respectivement.

Ce test suppose que s ₁ ² et s ₂ ² sont calculés à partir d’échantillons indépendants de taille n ₁ et n ₂ , tous deux issus de populations normalement distribuées.

Plus ce rapport est éloigné de un, plus les preuves de variances inégales au sein de la population sont fortes.

L’intervalle de confiance (1-α)100 % pour σ ² ₁ / σ ² ₂ est défini comme :

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

où F _{n 2 -1, n 1 -1, α/2} et F _{n 1 -1, n 2 -1, α/2}   sont les valeurs critiques de la distribution F pour le niveau de signification α choisi.

Les exemples suivants illustrent comment créer un intervalle de confiance pour σ ² ₁ / σ ² ₂ en utilisant trois méthodes différentes :

• Par la main
• Utiliser Microsoft Excel
• Utilisation du logiciel statistique R

Pour chacun des exemples suivants, nous utiliserons les informations suivantes :

• α = 0,05
• n ₁ = 16
• _n2 = 11
• s ₁ ² =28,2
• s ₂ ² = 19,3

Création manuelle d’un intervalle de confiance

Pour calculer manuellement un intervalle de confiance pour σ ² ₁ / σ ² ₂ , nous allons simplement insérer les nombres dont nous disposons dans la formule de l’intervalle de confiance :

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

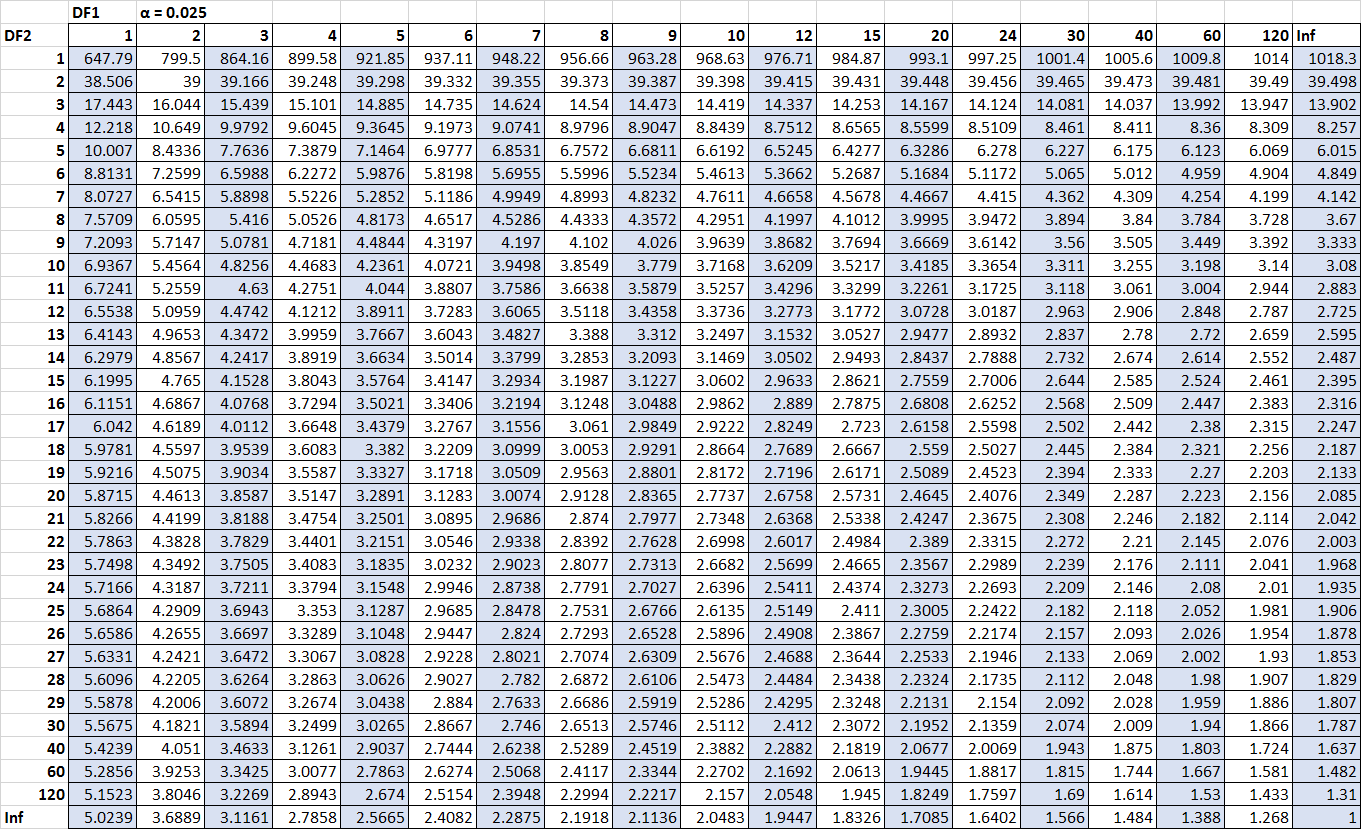
Les seuls chiffres qui nous manquent sont les valeurs critiques. Heureusement, nous pouvons localiser ces valeurs critiques dans le tableau de distribution F :

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Cliquez pour zoomer sur le tableau)

Nous pouvons maintenant intégrer tous les nombres dans la formule de l’intervalle de confiance :

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Ainsi, l’intervalle de confiance à 95 % pour le rapport des variances de la population est (0,4148, 4,4714) .

Création d’un intervalle de confiance à l’aide d’Excel

L’image suivante montre comment calculer un intervalle de confiance à 95 % pour le rapport des variances de la population dans Excel. Les limites inférieure et supérieure de l’intervalle de confiance sont affichées dans la colonne E et la formule utilisée pour trouver les limites inférieure et supérieure est affichée dans la colonne F :

Ainsi, l’intervalle de confiance à 95 % pour le rapport des variances de la population est (0,4148, 4,4714) . Cela correspond à ce que nous avons obtenu lorsque nous avons calculé manuellement l’intervalle de confiance.

Création d’un intervalle de confiance à l’aide de R

Le code suivant illustre comment calculer un intervalle de confiance à 95 % pour le rapport des variances de population dans R :

#define significance level, sample sizes, and sample variances
alpha <- .05
n1    <- 16
n2    <- 11
var1  <- 28.2
var2  <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Ainsi, l’intervalle de confiance à 95 % pour le rapport des variances de la population est (0,4148, 4,4714) . Cela correspond à ce que nous avons obtenu lorsque nous avons calculé manuellement l’intervalle de confiance.

Ressources additionnelles

Comment lire le tableau de distribution F
Comment trouver la valeur critique F dans Excel