Test U de Mann-Whitney
Un test U de Mann-Whitney (parfois appelé test de somme de rangs de Wilcoxon) est utilisé pour comparer les différences entre deux échantillons indépendants lorsque les distributions d’échantillons ne sont pas normalement distribuées et que les tailles d’échantillon sont petites (n <30).
Il est considéré comme l’équivalent non paramétrique du test t indépendant à deux échantillons .
Voici quelques exemples de cas où vous pouvez utiliser un test Mann-Whitney U :
- Vous souhaitez comparer les salaires de cinq diplômés de l’université A aux salaires de cinq diplômés de l’université B. Les salaires ne sont normalement pas distribués.
- Vous voulez savoir si la perte de poids varie pour deux groupes : 12 personnes utilisant le régime A et 10 personnes utilisant le régime B. La perte de poids n’est pas normalement répartie.
- Vous souhaitez savoir si les scores de 8 élèves de la classe A diffèrent de ceux de 7 élèves de la classe B. Les scores ne sont pas normalement distribués.
Dans chaque exemple, vous souhaitez comparer deux groupes, les distributions d’échantillonnage ne sont pas normales et les tailles d’échantillon sont petites.
Ainsi, un test U de Mann-Whitney est approprié tant que les hypothèses suivantes sont remplies.
Hypothèses du test U de Mann-Whitney
Avant d’effectuer un test Mann-Whitney U, vous devez vous assurer que les quatre hypothèses suivantes sont remplies :
- Ordinaire ou continu : la variable que vous analysez est ordinale ou continue. Des exemples de variables ordinales incluent les éléments de Likert (par exemple, une échelle de 5 points allant de « fortement en désaccord » à « tout à fait d’accord »). Des exemples de variables continues incluent la taille (mesurée en pouces), le poids (mesuré en livres) ou les résultats aux examens (mesurés de 0 à 100).
- Indépendance : Toutes les observations des deux groupes sont indépendantes les unes des autres.
- Forme : Les formes des distributions pour les deux groupes sont à peu près les mêmes.
Si ces hypothèses sont remplies, vous pouvez alors procéder à un test Mann-Whitney U.
Comment effectuer un test U de Mann-Whitney
Pour effectuer un test U de Mann-Whitney, nous suivons la procédure standard de test d’hypothèse en cinq étapes :
1. Énoncez les hypothèses.
Dans la plupart des cas, le test U de Mann-Whitney est réalisé sous forme de test bilatéral. Les hypothèses nulle et alternative s’écrivent sous la forme :
H 0 : Les deux populations sont égales
H a : Les deux populations ne sont pas égales
2. Déterminez un niveau de signification à utiliser pour l’hypothèse.
Décidez d’un niveau de signification. Les choix courants sont .01, .05 et .1.
3. Recherchez la statistique du test.
La statistique de test est notée U et est la plus petite de U 1 et U 2 , comme défini ci-dessous :
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
où n 1 et n 2 sont les tailles d’échantillon pour les échantillons 1 et 2 respectivement, et R 1 et R 2 sont la somme des rangs pour les échantillons 1 et 2 respectivement.
Les exemples ci-dessous montreront comment trouver cette statistique de test en détail.
4. Rejetez ou ne rejetez pas l’hypothèse nulle.
À l’aide des statistiques de test, déterminez si vous pouvez rejeter ou non l’hypothèse nulle en fonction du niveau de signification et de la valeur critique trouvés dans le tableau U de Mann-Whitney .
5. Interprétez les résultats.
Interpréter les résultats du test dans le contexte de la question posée.
Exemples de réalisation d’un test U de Mann-Whitney
Les exemples suivants montrent comment réaliser un test U de Mann-Whitney.
Exemple 1
Nous voulons savoir si un nouveau médicament est efficace ou non pour prévenir les crises de panique. Au total, 12 patients sont répartis au hasard en deux groupes de 6 et assignés à recevoir le nouveau médicament ou le placebo. Les patients enregistrent ensuite le nombre de crises de panique qu’ils ont subies au cours d’un mois.
Les résultats sont montrés plus bas:
| NOUVEAU MÉDICAMENT | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Effectuez un test Mann-Whitney U pour voir s’il existe une différence dans le nombre d’attaques de panique chez les patients du groupe placebo par rapport au groupe du nouveau médicament. Utilisez un niveau de signification de 0,05.
1. Énoncez les hypothèses.
H 0 : Les deux populations sont égales
H a : Les deux populations ne sont pas égales
2. Déterminez un niveau de signification à utiliser pour l’hypothèse.
Le problème nous dit que nous devons utiliser un niveau de signification de 0,05.
3. Recherchez la statistique du test.
Rappelons que la statistique de test est notée U et est la plus petite de U 1 et U 2 , comme défini ci-dessous :
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
où n 1 et n 2 sont les tailles d’échantillon pour les échantillons 1 et 2 respectivement, et R 1 et R 2 sont la somme des rangs pour les échantillons 1 et 2 respectivement.
Afin de trouver R 1 et R 2 , nous devons combiner les observations des deux groupes et les classer du plus petit au plus grand :
| NOUVEAU MÉDICAMENT | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Échantillon total : 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Rangs : 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = somme des rangs pour l’échantillon 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = somme des rangs pour l’échantillon 2 = 1,5+3+6,5+10+11+12 = 44
Ensuite, nous utilisons nos tailles d’échantillon n 1 et n 2 ainsi que notre somme des rangs R 1 et R 2 pour trouver U 1 et U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Nos statistiques de test sont la plus petite de U 1 et U 2 , qui se trouve être U = 13.
Remarque : Nous pourrions également utiliser la calculatrice du test U de Mann-Whitney pour déterminer que U = 13.
4. Rejetez ou ne rejetez pas l’hypothèse nulle.
En utilisant n 1 = 6 et n 2 = 6 avec un niveau de signification de 0,05, le tableau U de Mann-Whitney nous indique que la valeur critique est 5 :
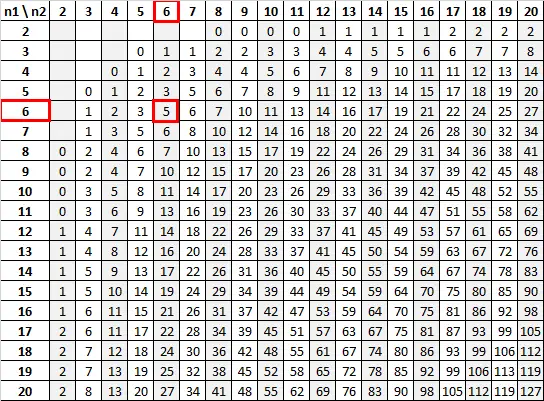
Puisque notre statistique de test (13) est supérieure à notre valeur critique (5), nous ne parvenons pas à rejeter l’hypothèse nulle.
5. Interprétez les résultats.
Puisque nous n’avons pas réussi à rejeter l’hypothèse nulle, nous ne disposons pas de preuves suffisantes pour affirmer que le nombre d’attaques de panique ressenties par les patients du groupe placebo est différent de celui du groupe du nouveau médicament.
Exemple 2
Nous voulons savoir si étudier 30 minutes par jour pendant une semaine aide les étudiants à obtenir de meilleurs résultats à un test. Au total, 15 patients sont répartis au hasard dans un groupe d’étude ou sans étude. Après une semaine, tous les étudiants passent le même test.
Les résultats des tests pour les deux groupes sont présentés ci-dessous :
| ÉTUDE | PAS D’ÉTUDE |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Effectuez un test Mann-Whitney U pour voir s’il y a une différence dans les résultats des tests pour le groupe d’étude par rapport au groupe sans étude. Utilisez un niveau de signification de 0,01.
1. Énoncez les hypothèses.
H 0 : Les deux populations sont égales
H a : Les deux populations ne sont pas égales
2. Déterminez un niveau de signification à utiliser pour l’hypothèse.
Le problème nous dit que nous devons utiliser un niveau de signification de 0,01.
3. Recherchez la statistique du test.
Rappelons que la statistique de test est notée U et est la plus petite de U 1 et U 2 , comme défini ci-dessous :
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
où n 1 et n 2 sont les tailles d’échantillon pour les échantillons 1 et 2 respectivement, et R 1 et R 2 sont la somme des rangs pour les échantillons 1 et 2 respectivement.
Afin de trouver R 1 et R 2 , nous devons combiner les observations des deux groupes et les classer du plus petit au plus grand :
| ÉTUDE | PAS D’ÉTUDE |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Échantillon total : 72 , 75 , 80 , 81 , 84 , 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Rangs : 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = somme des rangs pour l’échantillon 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = somme des rangs pour l’échantillon 2 = 1+2+3+4+6+11+13 = 40
Ensuite, nous utilisons nos tailles d’échantillon n 1 et n 2 ainsi que notre somme des rangs R 1 et R 2 pour trouver U 1 et U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Nos statistiques de test sont la plus petite de U 1 et U 2 , qui se trouve être U = 12.
Remarque : Nous pourrions également utiliser la calculatrice du test U de Mann-Whitney pour déterminer que U = 12.
4. Rejetez ou ne rejetez pas l’hypothèse nulle.
En utilisant n 1 = 8 et n 2 = 7 avec un niveau de signification de 0,01, le tableau U de Mann-Whitney nous indique que la valeur critique est 6 :
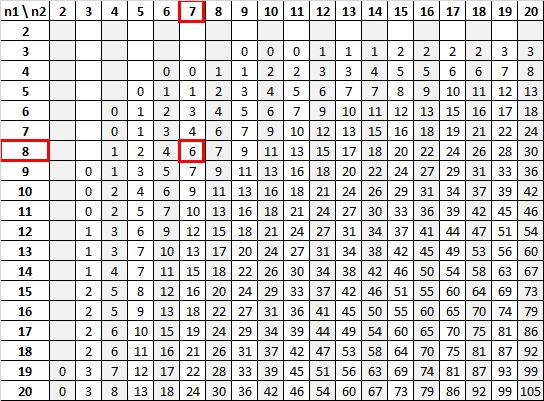
Puisque notre statistique de test (12) est supérieure à notre valeur critique (6), nous ne parvenons pas à rejeter l’hypothèse nulle.
5. Interprétez les résultats.
Puisque nous n’avons pas réussi à rejeter l’hypothèse nulle, nous ne disposons pas de preuves suffisantes pour affirmer que les résultats aux tests des étudiants qui ont étudié sont différents de ceux des étudiants qui n’ont pas étudié.
Ressources additionnelles
Calculateur de test U de Mann-Whitney
Tableau U Mann-Whitney
Comment effectuer un test Mann-Whitney U dans Excel
Comment effectuer un test U de Mann-Whitney dans R
Comment effectuer un test Mann-Whitney U en Python
Comment effectuer un test Mann-Whitney U dans SPSS
Comment effectuer un test Mann-Whitney U dans Stata
