Types de méthodes d’échantillonnage (avec exemples)
Les chercheurs souhaitent souvent répondre à des questions sur les populations telles que :
- Quelle est la hauteur moyenne d’une certaine espèce de plante ?
- Quel est le poids moyen d’une certaine espèce d’oiseau ?
- Quel pourcentage de citoyens dans une certaine ville soutiennent une certaine loi ?
Une façon de répondre à ces questions consiste à collecter des données sur chaque individu de la population d’intérêt.
Cependant, cela est généralement trop coûteux et prend trop de temps, c’est pourquoi les chercheurs prélèvent plutôt un échantillon de la population et utilisent les données de l’échantillon pour tirer des conclusions sur la population dans son ensemble.

Il existe de nombreuses méthodes différentes que les chercheurs peuvent potentiellement utiliser pour obtenir que des individus fassent partie d’un échantillon. Celles-ci sont connues sous le nom de méthodes d’échantillonnage .
Dans cet article, nous partageons les méthodes d’échantillonnage les plus couramment utilisées en statistique, y compris les avantages et les inconvénients des différentes méthodes.
Méthodes d’échantillonnage probabiliste
La première classe de méthodes d’échantillonnage est connue sous le nom de méthodes d’échantillonnage probabiliste , car chaque membre d’une population a une probabilité égale d’être sélectionné pour faire partie de l’échantillon.
Échantillon aléatoire simple
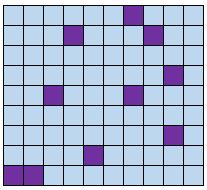
Définition : Chaque membre d’une population a une chance égale d’être sélectionné pour faire partie de l’échantillon. Sélectionnez les membres au hasard en utilisant un générateur de nombres aléatoires ou un moyen de sélection aléatoire.
Exemple : Nous mettons les noms de chaque élève d’une classe dans un chapeau et tirons au hasard les noms pour obtenir un échantillon d’élèves.
Avantage : les échantillons aléatoires simples sont généralement représentatifs de la population qui nous intéresse puisque chaque membre a une chance égale d’être inclus dans l’échantillon.
Échantillon aléatoire stratifié
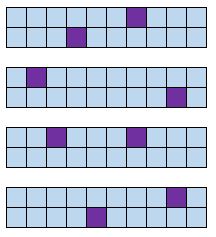
Définition : Diviser une population en groupes. Sélectionnez au hasard quelques membres de chaque groupe pour faire partie de l’échantillon.
Exemple : répartissez tous les élèves d’une école en fonction de leur niveau : étudiants de première année, étudiants de deuxième année, juniors et seniors. Demandez à 50 élèves de chaque année de répondre à une enquête sur les repas scolaires.
Avantage : Des échantillons aléatoires stratifiés garantissent que les membres de chaque groupe de la population sont inclus dans l’enquête.
Échantillon aléatoire en grappes
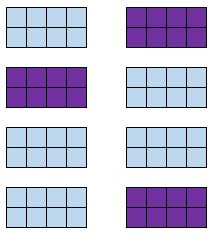
Définition : Diviser une population en grappes. Sélectionnez au hasard certaines des grappes et incluez tous les membres de ces grappes dans l’échantillon.
Exemple : Une entreprise qui propose des excursions d’observation des baleines souhaite interroger ses clients. Sur dix circuits qu’ils proposent par jour, ils sélectionnent au hasard quatre circuits et interrogent chaque client sur son expérience.
Avantage : les échantillons aléatoires en grappes rassemblent tous les membres de certains groupes, ce qui est utile lorsque chaque groupe reflète la population dans son ensemble.
Échantillon aléatoire systématique
![]()
Définition : Mettre chaque membre d’une population dans un certain ordre. Choisir un point de départ aléatoire et sélectionner chaque n ième membre pour faire partie de l’échantillon.
Exemple : un enseignant classe les élèves par ordre alphabétique en fonction de leur nom de famille, choisit au hasard un point de départ et choisit un élève sur cinq pour faire partie de l’échantillon.
Avantage : les échantillons aléatoires systématiques sont généralement représentatifs de la population qui nous intéresse puisque chaque membre a une chance égale d’être inclus dans l’échantillon.
Méthodes d’échantillonnage non probabilistes
Une autre classe de méthodes d’échantillonnage est connue sous le nom de méthodes d’échantillonnage non probabilistes , car tous les membres d’une population n’ont pas la même probabilité d’être sélectionnés pour faire partie de l’échantillon.
Ce type de méthode d’échantillonnage est parfois utilisé car il est beaucoup moins cher et plus pratique que les méthodes d’échantillonnage probabiliste. Il est souvent utilisé lors d’analyses exploratoires lorsque les chercheurs souhaitent simplement acquérir une première compréhension d’une population.
Cependant, les échantillons résultant de ces méthodes d’échantillonnage ne peuvent pas être utilisés pour tirer des conclusions sur les populations dont ils sont issus, car ils ne constituent généralement pas des échantillons représentatifs.
Échantillon de commodité
Définition : Choisir les membres d’une population facilement disponibles pour être inclus dans l’échantillon.
Exemple : un chercheur se tient devant une bibliothèque pendant la journée et interroge les passants.
Inconvénient : le lieu et l’heure de la journée affecteront les résultats. Il est plus que probable que l’échantillon souffrira d’ un biais de sous-dénombrement puisque certaines personnes (par exemple celles qui travaillent pendant la journée) ne seront pas autant représentées dans l’échantillon.
Échantillon de réponse volontaire
Définition : Un chercheur demande à des volontaires d’être inclus dans une étude et les membres d’une population décident volontairement d’être inclus dans l’échantillon ou non.
Exemple : un animateur de radio demande aux auditeurs d’aller en ligne et de répondre à un sondage sur son site Web.
Inconvénient : les personnes qui répondent volontairement auront probablement des opinions plus fortes (positives ou négatives) que le reste de la population, ce qui en fait un échantillon non représentatif. En utilisant cette méthode d’échantillonnage, l’échantillon est susceptible de souffrir d’ un biais de non-réponse – certains groupes de personnes sont tout simplement moins susceptibles de fournir des réponses.
Échantillon de boule de neige
Définition : Les chercheurs recrutent des sujets initiaux pour participer à une étude, puis demandent à ces sujets initiaux de recruter des sujets supplémentaires pour participer à l’étude. En utilisant cette approche, la taille de l’échantillon « fait boule de neige » de plus en plus grande à mesure que chaque sujet supplémentaire recrute plus de sujets.
Exemple : Des chercheurs mènent une étude sur des personnes atteintes de maladies rares, mais il est difficile de trouver des personnes réellement atteintes de la maladie. Cependant, s’ils parviennent à trouver seulement quelques personnes initiales pour participer à l’étude, ils peuvent alors leur demander de recruter d’autres personnes qu’ils pourraient connaître par le biais d’un groupe de soutien privé ou par d’autres moyens.
Inconvénient : un biais d’échantillonnage est susceptible de se produire. Étant donné que les sujets initiaux recrutent des sujets supplémentaires, il est probable que de nombreux sujets partageront des traits ou des caractéristiques similaires qui pourraient ne pas être représentatifs de la population plus large étudiée. Ainsi, les résultats de l’échantillon ne peuvent pas être extrapolés à la population.
En savoir plus sur l’échantillonnage boule de neige ici .
Échantillon délibéré
Définition : Les chercheurs recrutent des individus en fonction de ceux qui, selon eux, seront les plus utiles en fonction de l’objectif de leur étude.
Exemple : les chercheurs souhaitent connaître les opinions des habitants d’une ville sur l’installation potentielle d’une nouvelle salle d’escalade sur la place de la ville. Ils recherchent donc délibérément des personnes qui fréquentent d’autres salles d’escalade de la ville.
Inconvénient : il est peu probable que les individus de l’échantillon soient représentatifs de la population globale. Ainsi, les résultats de l’échantillon ne peuvent pas être extrapolés à la population.
