Mesures de tendance centrale : définition & Exemples
Une mesure de tendance centrale est une valeur unique qui représente le point central d’un ensemble de données. Cette valeur peut également être appelée « l’emplacement central » d’un ensemble de données.
En statistiques, il existe trois mesures courantes de tendance centrale :
- La moyenne
- La médiane
- La mode
Chacune de ces mesures trouve l’emplacement central d’un ensemble de données en utilisant différentes méthodes. Selon le type de données que vous analysez, il peut être préférable d’utiliser l’une de ces trois mesures plutôt que les deux autres.
Dans cet article, nous verrons comment calculer chacune des trois mesures de tendance centrale ainsi que comment déterminer quelle mesure est la meilleure à utiliser en fonction de vos données.
Pourquoi les mesures de tendance centrale sont-elles utiles ?
Avant de voir comment calculer la moyenne, la médiane et le mode, il est utile de comprendre pourquoi ces mesures sont réellement utiles en premier lieu.
Considérez le scénario suivant :
Un jeune couple essaie de décider où acheter sa première maison dans une nouvelle ville et le maximum qu’il peut dépenser est de 150 000 $. Certains quartiers de la ville ont des maisons chères, d’autres des maisons bon marché et d’autres encore des maisons de prix moyen. Ils souhaitent affiner facilement leur recherche à des quartiers spécifiques qui correspondent à leur budget.
Si le couple se contentait de regarder les prix des maisons individuelles dans chaque quartier, il pourrait avoir du mal à déterminer quels quartiers correspondent le mieux à son budget, car il pourrait voir quelque chose comme ceci :
Prix des maisons du quartier A : 140 000 $, 190 000 $, 265 000 $, 115 000 $, 270 000 $, 240 000 $, 250 000 $, 180 000 $, 160 000 $, 200 000 $, 240 000 $, 280 000 $,…
Prix des maisons du quartier B : 140 000 $, 290 000 $, 155 000 $, 165 000 $, 280 000 $, 220 000 $, 155 000 $, 185 000 $, 160 000 $, 200 000 $, 190 000 $, 140 000 $, 145 000 $,…
Prix des maisons du quartier C : 140 000 $, 130 000 $, 165 000 $, 115 000 $, 170 000 $, 100 000 $, 150 000 $, 180 000 $, 190 000 $, 120 000 $, 110 000 $, 130 000 $, 120 000 $,…
Cependant, s’ils connaissaient le prix moyen (par exemple une mesure de la tendance centrale) des maisons dans chaque quartier, ils pourraient alors affiner leur recherche beaucoup plus rapidement car ils pourraient plus facilement identifier quel quartier a des prix de maisons qui correspondent à leur budget :
Prix moyen d’une maison dans le quartier A : 220 000 $
Prix moyen d’une maison dans le quartier B : 190 000 $
Prix moyen d’une maison dans le quartier C : 140 000 $
En connaissant le prix moyen des maisons dans chaque quartier, ils peuvent rapidement voir que le quartier C est susceptible d’avoir le plus de maisons disponibles dans les limites de leur budget.
C’est l’avantage d’utiliser une mesure de tendance centrale : elle vous aide à comprendre la valeur centrale d’un ensemble de données, qui tend à décrire où se situent généralement les valeurs des données. Dans cet exemple particulier, cela aide le jeune couple à comprendre le prix typique d’une maison dans chaque quartier.
À retenir : une mesure de tendance centrale est utile car elle nous fournit une valeur unique qui décrit le « centre » d’un ensemble de données. Cela nous aide à comprendre un ensemble de données beaucoup plus rapidement qu’en examinant simplement toutes les valeurs individuelles de l’ensemble de données.
Signifier
La mesure de tendance centrale la plus couramment utilisée est la moyenne . Pour calculer la moyenne d’un ensemble de données, il vous suffit d’additionner toutes les valeurs individuelles et de diviser par le nombre total de valeurs.
Moyenne = (somme de toutes les valeurs) / (nombre total de valeurs)
Par exemple, supposons que nous ayons l’ensemble de données suivant qui montre le nombre de circuits réussis par 10 joueurs de baseball de la même équipe au cours d’une saison :
| Joueur | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dix |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Le nombre moyen de circuits réussis par joueur peut être calculé comme suit :
Moyenne = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 circuits .
Médian
La médiane est la valeur médiane d’un ensemble de données. Vous pouvez trouver la médiane en classant toutes les valeurs individuelles dans un ensemble de données de la plus petite à la plus grande et en trouvant la valeur médiane. S’il y a un nombre impair de valeurs, la médiane est la valeur médiane. S’il existe un nombre pair de valeurs, la médiane est la moyenne des deux valeurs médianes.
Par exemple, pour trouver le nombre médian de circuits réussis par les 10 joueurs de baseball dans l’exemple précédent, nous pouvons classer les joueurs par ordre décroissant du nombre de circuits réussis :
| Joueur | #1 | #6 | #7 | #5 | #dix | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Puisque nous avons un nombre pair de valeurs, la médiane est simplement la moyenne des deux valeurs médianes : 13,5 .
Considérons plutôt si nous avions neuf joueurs :
| Joueur | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
Dans ce cas, puisque nous avons un nombre impair de valeurs, la médiane est simplement la valeur médiane : 14 .
La mode
Le mode est la valeur qui apparaît le plus souvent dans un ensemble de données. Un ensemble de données peut n’avoir aucun mode (si aucune valeur ne se répète), un mode ou plusieurs modes.
Par exemple, l’ensemble de données suivant n’a pas de mode :
| Joueur | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dix |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
L’ensemble de données suivant a un mode : 15 . C’est la valeur qui apparaît le plus fréquemment.
| Joueur | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dix |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
L’ensemble de données suivant a trois modes : 8, 15, 19 . Ce sont les valeurs qui apparaissent le plus fréquemment.
| Joueur | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dix |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Le mode peut être une mesure particulièrement utile de la tendance centrale lorsque l’on travaille avec des données catégorielles, car il nous indique quelle catégorie apparaît le plus fréquemment. Par exemple, considérons le graphique à barres suivant qui montre les résultats d’une enquête sur la couleur préférée des gens :
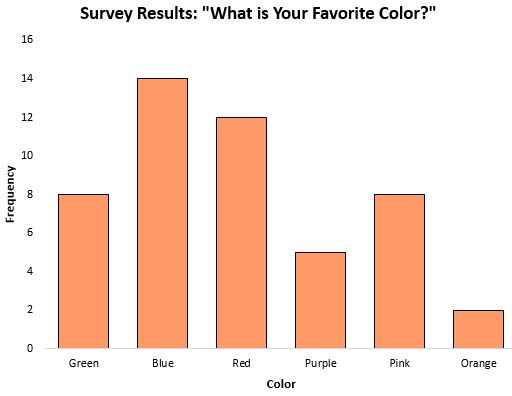
Le mode , ou la réponse qui s’est produite le plus fréquemment, était bleu.
Dans les scénarios où les données sont catégoriques (comme celui ci-dessus), il n’est même pas possible de calculer la médiane ou la moyenne, le mode est donc la seule mesure de tendance centrale que nous pouvons utiliser.
Le mode peut également être utilisé pour des données numériques, comme nous l’avons vu dans l’exemple ci-dessus avec des joueurs de baseball. Cependant, le mode a tendance à être moins utile pour répondre à la question « Quelle est une valeur typique pour cet ensemble de données ? »
Par exemple, supposons que nous souhaitions connaître le nombre typique de circuits réussis par un joueur de baseball de cette équipe :
| Joueur | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dix |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Le mode de cet ensemble de données est 8, 15 et 19, car ce sont les valeurs les plus fréquentes. Cependant, ceux-ci ne sont pas très utiles pour comprendre le nombre typique de circuits réussis par un joueur de l’équipe. Une meilleure mesure de la tendance centrale serait dans ce cas la médiane (15) ou la moyenne (également 15).
Le mode est également une mauvaise mesure de la tendance centrale lorsqu’il s’agit d’un nombre éloigné du reste des valeurs. Par exemple, le mode de l’ensemble de données suivant est 30, mais cela ne représente pas réellement le nombre « typique » de circuits réussis par joueur de l’équipe :
| Joueur | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dix |
|---|---|---|---|---|---|---|---|---|---|---|
| Coups de circuit | 5 | 6 | 7 | dix | 11 | 12 | 13 | 15 | 30 | 30 |
Encore une fois, la moyenne ou la médiane ferait un meilleur travail pour décrire l’emplacement central de cet ensemble de données.
Quand utiliser la moyenne, la médiane et le mode
Nous avons vu que la moyenne, la médiane et le mode mesurent tous l’emplacement central, ou la « valeur typique », d’un ensemble de données de manières très différentes :
Moyenne : recherche la valeur moyenne dans un ensemble de données.
Médiane : recherche la valeur médiane dans un ensemble de données.
Mode : recherche la valeur la plus fréquente dans un ensemble de données.
Voici les scénarios dans lesquels certaines mesures de tendance centrale sont préférables à utiliser que d’autres :
Quand utiliser la moyenne
Il est préférable d’utiliser la moyenne lorsque la distribution des données est assez symétrique et qu’il n’y a pas de valeurs aberrantes.
Par exemple, supposons que nous ayons la distribution suivante qui montre les salaires des individus dans une certaine ville :

Étant donné que cette distribution est assez symétrique (c’est-à-dire que si vous la divisez en deux, chaque moitié semblerait à peu près égale) et qu’il n’y a pas de valeurs aberrantes (c’est-à-dire pas de salaires extrêmement élevés), la moyenne fera un bon travail pour décrire cet ensemble de données.
La moyenne s’avère être de 63 000 $, ce qui se situe à peu près au centre de la distribution :

Quand utiliser la médiane
Il est préférable d’utiliser la médiane lorsque la distribution des données est asymétrique ou lorsqu’il existe des valeurs aberrantes.
Données biaisées :
Lorsque la distribution est asymétrique, la médiane parvient toujours à capturer l’emplacement central. Par exemple, considérons la répartition suivante des salaires des individus dans une certaine ville :

La médiane rend mieux compte du salaire « typique » d’un individu que la moyenne. En effet, les valeurs élevées à la queue d’une distribution ont tendance à éloigner la moyenne du centre et vers la longue queue.
Dans cet exemple particulier, la moyenne nous indique qu’un individu typique gagne environ 47 000 $ par an dans cette ville, tandis que la médiane nous indique que l’individu typique ne gagne qu’environ 32 000 $ par an, ce qui est beaucoup plus représentatif de l’individu type.
Valeurs aberrantes :
La médiane permet également de mieux capturer l’emplacement central d’une distribution lorsqu’il existe des valeurs aberrantes dans les données. Par exemple, considérons le graphique suivant qui montre la superficie en pieds carrés des maisons dans une certaine rue :

La moyenne est fortement influencée par quelques maisons extrêmement grandes, alors que la médiane ne l’est pas. Ainsi, la médiane parvient mieux à capturer la superficie « typique » d’une maison dans cette rue que la moyenne.
Quand utiliser le mode
Il est préférable d’utiliser ce mode lorsque vous travaillez avec des données catégorielles et que vous souhaitez savoir quelle catégorie apparaît le plus fréquemment. Voici quelques exemples :
- Vous menez une enquête sur les couleurs préférées des gens et vous souhaitez savoir quelle couleur apparaît le plus fréquemment dans les réponses.
- Vous menez une enquête sur les préférences des gens parmi trois choix pour la conception d’un site Web et vous souhaitez savoir quel design les gens préfèrent le plus.
Comme mentionné précédemment, si vous travaillez avec des données catégorielles, il n’est même pas possible de calculer la médiane ou la moyenne, ce qui laisse le mode comme seule mesure de la tendance centrale.
En général, si vous travaillez avec des données numériques telles que la superficie des maisons, le nombre de circuits réussis par joueur, le salaire par individu, etc., il est généralement préférable d’utiliser la médiane ou la moyenne pour décrire la valeur « typique » dans l’ensemble de données.
Remarque : Il est important de noter que si un ensemble de données est parfaitement distribué normalement, alors la moyenne, la médiane et le mode ont tous la même valeur.
