Qualité de l’ajustement
Cet article explique ce qu’est la qualité de l’ajustement dans les statistiques. De même, il montre comment mesurer la qualité de l’ajustement d’un modèle de régression et, en plus, vous pourrez voir un exercice résolu de la qualité de l’ajustement.
Qu’est-ce que la qualité de l’ajustement ?
En statistique, la qualité de l’ajustement est le degré d’ajustement d’un modèle de régression à l’échantillon de données. Autrement dit, la qualité de l’ajustement d’un modèle de régression fait référence au niveau de couplage entre l’ensemble d’observations et les valeurs obtenues grâce à la régression.
Par conséquent, plus la qualité de l’ajustement d’un modèle de régression est élevée, mieux il explique les données étudiées. Ainsi, nous souhaitons que le modèle statistique soit le plus ajusté, mieux c’est.
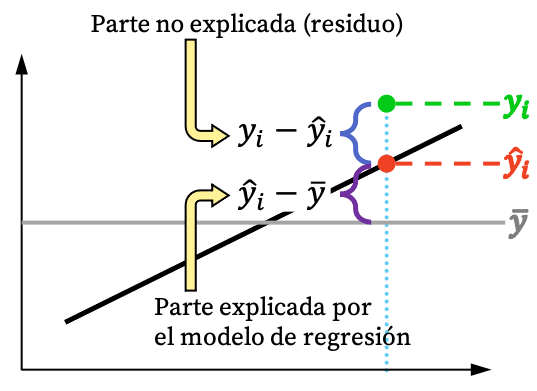
Comme vous pouvez le voir sur l’image ci-dessus, la valeur d’une observation ne peut généralement pas être entièrement expliquée par le modèle de régression. Mais logiquement, plus le modèle de régression peut expliquer à partir de l’ensemble de données, plus le modèle sera adapté. Bref, nous nous intéressons à un modèle de régression le plus serré possible.
Qualité de l’ajustement d’un modèle de régression
Pour déterminer la qualité de l’ajustement d’un modèle de régression, on utilise généralement le coefficient de détermination , qui est un coefficient statistique qui indique le pourcentage expliqué par le modèle de régression. Ainsi, plus le coefficient de détermination d’un modèle est élevé, plus le modèle sera adapté à l’échantillon de données.
![]()
Cependant, il convient de noter que plus un modèle de régression comporte de variables, plus son coefficient de détermination sera élevé. Pour cette raison, le coefficient de détermination ajusté est également souvent utilisé pour mesurer la qualité de l’ajustement d’un modèle. Le coefficient de détermination ajusté est une variation du coefficient précédent qui indique le pourcentage expliqué par le modèle de régression, pénalisant pour chaque variable explicative incluse dans le modèle.
![]()
Il est donc préférable d’utiliser le coefficient de détermination ajusté pour comparer deux modèles comportant un certain nombre de variables différentes, car il prend en compte le nombre de variables incluses dans le modèle.
Enfin, il convient de noter que le test du Chi carré peut également être utilisé pour mesurer la qualité de l’ajustement d’un modèle de régression, même si les valeurs des deux coefficients précédents sont généralement utilisées.
Exemple concret de bon ajustement
Pour finir, nous allons voir un exercice résolu de qualité d’ajustement pour finir d’assimiler ce concept statistique.
- Avec la même série de données, deux modèles de régression linéaire différents sont réalisés, dont vous pouvez voir les résultats dans le tableau suivant. Quel modèle est-il préférable d’utiliser ?
| Modèle de régression 1 | Modèle de régression 2 | |
|---|---|---|
| Coefficient de détermination | 57% | 64% |
| Coefficient de détermination ajusté | 49% | 43% |
| Nombre de variables explicatives | 3 | 7 |
Dans ce cas, nous supposons que les deux modèles satisfont aux hypothèses précédentes des modèles de régression linéaire et, par conséquent, il nous suffit d’analyser la qualité de l’ajustement des modèles.
Le modèle de régression 2 a un coefficient de détermination plus élevé que le modèle de régression 1, il semble donc a priori être un meilleur modèle de régression puisqu’il est capable de mieux expliquer l’échantillon de données.
Cependant, le modèle de régression 2 comporte 7 variables indépendantes dans le modèle, tandis que le modèle de régression 1 n’en comporte que 3. Le modèle 2 sera donc beaucoup plus compliqué et plus difficile à interpréter que le premier modèle.
De plus, si nous examinons le coefficient de détermination ajusté, qui prend en compte le nombre de variables dans le modèle, le modèle de régression 1 a un coefficient de détermination ajusté plus élevé que le modèle de régression 2.
En conclusion, il est préférable d’utiliser le modèle de régression 1, puisque son coefficient de détermination ajusté est supérieur à celui du modèle de régression 2. Bien que le modèle de régression 2 ait un coefficient de détermination non ajusté plus élevé, c’est parce qu’ils ont inclus beaucoup plus de variables dans le modèle de régression 1. modèle, ce qui augmente la valeur dudit coefficient mais rend l’interprétation du modèle plus difficile et, sûrement, fait que la prédiction d’une nouvelle valeur est pire.
Pour comparer des modèles avec différents nombres de variables, il est préférable d’utiliser le coefficient de détermination ajusté car il pénalise pour chaque variable ajoutée au modèle. Comme vous l’avez vu dans cet exemple, selon le coefficient de détermination non ajusté, le modèle de régression 2 est meilleur, cependant, grâce au coefficient de détermination ajusté, nous pouvons savoir que le modèle de régression 1 est en réalité meilleur.
