Régression logistique

Par Pr Amélia Rodriguez août 2, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la régression logistique dans les statistiques. De même, vous trouverez la formule de régression logistique, quels sont les différents types de régression logistique et, en plus, un exercice de régression logistique résolu.

Qu’est-ce que la régression logistique ?

En statistiques, la régression logistique est un type de modèle de régression utilisé pour prédire le résultat d’une variable catégorielle . Autrement dit, la régression logistique est utilisée pour modéliser la probabilité qu’une variable catégorielle prenne une certaine valeur en fonction des variables indépendantes.

Le modèle de régression logistique le plus courant est la régression logistique binaire, dans laquelle il n’y a que deux résultats possibles : « échec » ou « succès » ( distribution de Bernoulli ). « L’échec » est représenté par la valeur 0, tandis que le « succès » est représenté par la valeur 1.

Par exemple, la probabilité qu’un étudiant réussisse un examen en fonction des heures qu’il a consacrées à étudier peut être étudiée à l’aide d’un modèle de régression logistique. Dans ce cas, l’échec serait le résultat d’un « échec » et, d’un autre côté, la réussite serait le résultat d’un « succès ».

Formule de régression logistique

L’équation d’un modèle de régression logistique est la suivante :

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

Par conséquent, dans un modèle de régression logistique, la probabilité d’obtenir le résultat « succès », c’est-à-dire que la variable dépendante prenne la valeur 1, est calculée avec la formule suivante :

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

Où:

$p$ est la probabilité que la variable dépendante vaille 1.
$\beta_0$ est la constante du modèle de régression logistique.
$\beta_i$ est le coefficient de régression de la variable i.
$x_i$ est la valeur de la variable i.

Exemple de modèle de régression logistique

Maintenant que nous connaissons la définition de la régression logistique, voyons un exemple concret de la façon de créer un modèle de ce type de régression.

Dans le tableau suivant, une série de 20 données ont été compilées qui relient les heures d’étude de chaque étudiant et s’il a réussi ou échoué à un examen de statistiques. Effectuez un modèle de régression logistique et calculez la probabilité qu’un élève réussisse s’il a étudié 4 heures.

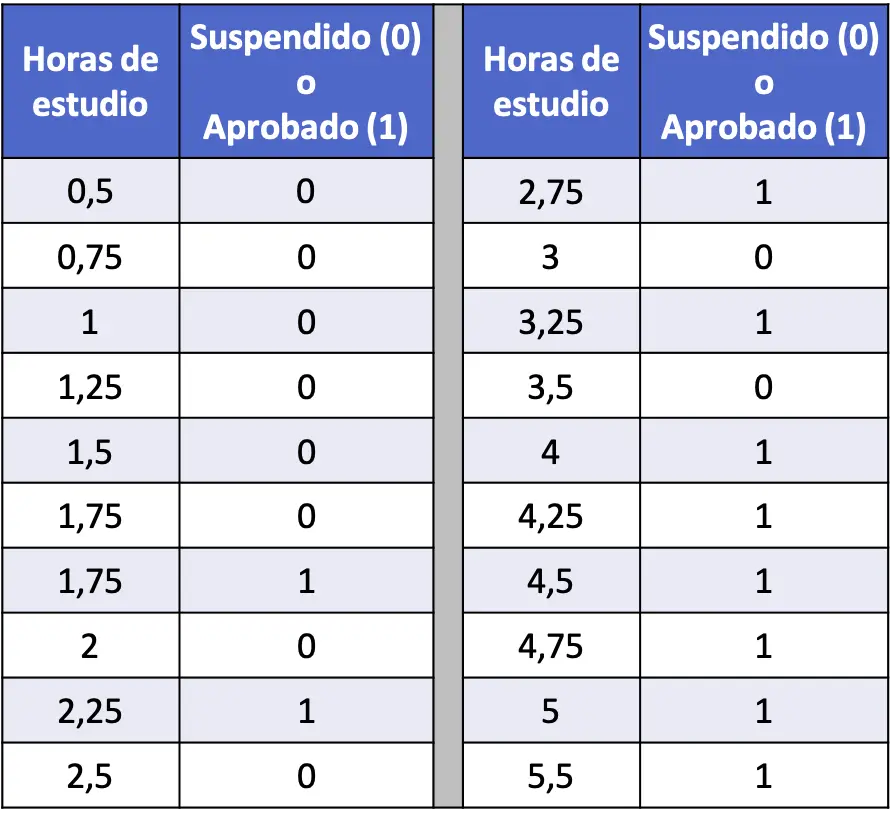
Dans ce cas, la variable explicative est le nombre d’heures d’études et la variable de réponse est si l’étudiant a échoué (0) ou réussi (1). Par conséquent, dans notre modèle nous n’aurons que le coefficient

$\beta_0$ et le coefficient $\beta_1$ , puisqu’il n’y a qu’une seule variable indépendante.

$\beta_0 \qquad \beta_1$

La détermination manuelle des coefficients de régression est très laborieuse, il est donc recommandé d’utiliser un logiciel informatique tel que Minitab. Ainsi, les valeurs des coefficients de régression calculés à l’aide de Minitab sont les suivantes :

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

Le modèle de régression logistique est donc le suivant :

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

Ci-dessous, vous pouvez voir l’échantillon de données et l’équation du modèle de régression logistique représenté graphiquement :

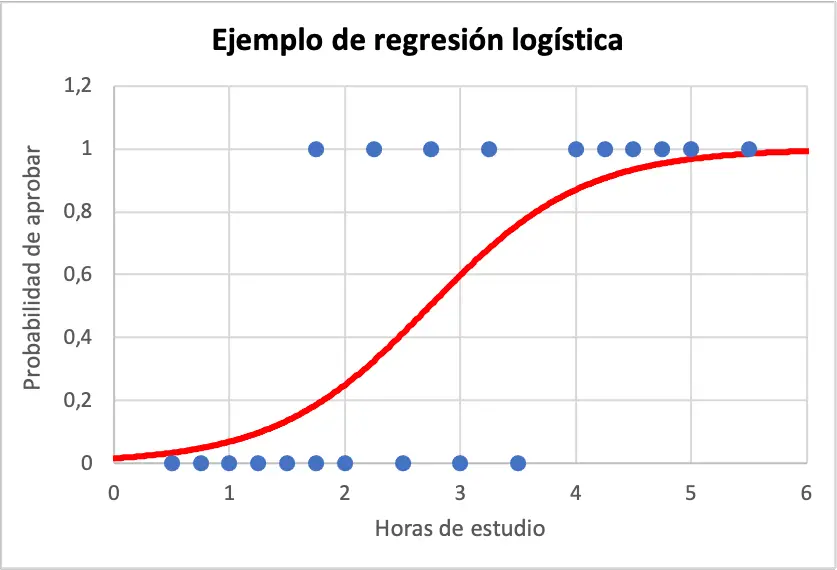
Ainsi, pour calculer la probabilité qu’un étudiant réussisse s’il a étudié 4 heures, il suffit d’utiliser l’équation obtenue à partir du modèle de régression logistique :

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

En bref, si un étudiant étudie quatre heures, il aura une probabilité de 86,99 % de réussir l’examen.

Types de régression logistique

Il existe trois types de régression logistique :

Régression logistique binaire : La variable dépendante ne peut avoir que deux valeurs (0 et 1).
Régression logistique multinomiale : La variable dépendante a plus de deux valeurs possibles.
Régression logistique ordinale : les résultats possibles présentent un ordre naturel.

Régression logistique et régression linéaire

Enfin, en résumé, nous verrons quelle est la différence entre une régression logistique et une régression linéaire, puisque le modèle de régression le plus utilisé en statistique est le modèle linéaire.

La régression linéaire est utilisée pour modéliser les variables dépendantes numériques. De plus, dans la régression linéaire, la relation entre les variables explicatives et la variable de réponse est linéaire.

Par conséquent, la principale différence entre la régression logistique et la régression linéaire réside dans le type de variable dépendante. Dans une régression logistique, la variable dépendante est catégorielle, alors que la variable dépendante dans une régression linéaire est numérique.

Ainsi, la régression logistique est utilisée pour prédire un résultat entre deux options possibles, tandis que la régression linéaire permet de prédire un résultat numérique.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus