Intervalle de confiance pour la différence des moyennes
Cet article explique ce qu’est un intervalle de confiance pour la différence de moyennes dans les statistiques et à quoi il sert. Ainsi, vous découvrirez comment calculer l’intervalle de confiance pour la différence de deux moyennes et un exercice résolu étape par étape.
Quel est l’intervalle de confiance pour la différence de moyennes ?
L’ intervalle de confiance pour la différence des moyennes est un intervalle qui fournit une valeur maximale et une valeur minimale entre lesquelles se situe la valeur de la différence des moyennes de deux populations avec un certain niveau de confiance.
Par exemple, si l’intervalle de confiance pour la différence des moyennes de deux populations avec un niveau de confiance de 95 % est (3,5), cela signifie que la différence entre les moyennes des deux populations sera comprise entre 3 et 5 avec une probabilité de 95 %.
Par conséquent, en statistique, l’intervalle de confiance pour la différence des moyennes est utilisé pour estimer deux valeurs entre lesquelles se situe la différence entre deux moyennes de population. Ainsi, à partir des données de deux échantillons, il est possible d’approcher la différence entre les moyennes des populations.
Formule d’intervalle de confiance pour la différence de moyennes
La formule de l’intervalle de confiance pour la différence des moyennes dépend du fait que les variances de la population soient connues ou non et, dans le cas contraire, de la question de savoir si les variances de la population peuvent être supposées égales ou non. Nous verrons donc ensuite comment l’intervalle de confiance pour la différence des moyennes est calculé dans chaque cas.
écarts connus
La formule pour calculer l’intervalle de confiance pour la différence des moyennes lorsque les variances des deux populations sont connues avec un niveau de confiance de 1-α est la suivante :
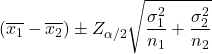
Où:
 est la moyenne de l’échantillon i.
est la moyenne de l’échantillon i. est l’écart type de la population i.
est l’écart type de la population i. est la valeur de la distribution normale standard avec une probabilité α/2.
est la valeur de la distribution normale standard avec une probabilité α/2. est la taille de l’échantillon i.
est la taille de l’échantillon i.
Ce cas est le moins courant, puisque la valeur des variances de population est généralement inconnue.
variances inconnues et égales
Lorsque les variances des deux populations sont inconnues mais peuvent être estimées égales, la formule de calcul de l’intervalle de confiance pour la différence des moyennes avec un niveau de confiance de 1-α est la suivante :
![]()
Où:
 est la moyenne de l’échantillon i.
est la moyenne de l’échantillon i. est l’écart type regroupé.
est l’écart type regroupé. est la valeur de la distribution t de Student de n 1 + n 2 -2 degrés de liberté avec une probabilité de α/2.
est la valeur de la distribution t de Student de n 1 + n 2 -2 degrés de liberté avec une probabilité de α/2. est la taille de l’échantillon i.
est la taille de l’échantillon i.
Puisque dans ce cas, on suppose que les variances de la population sont équivalentes, l’écart type combiné est utilisé pour calculer l’intervalle de confiance, qui est calculé avec la formule suivante :

Où
![]() est l’écart type de l’échantillon i.
est l’écart type de l’échantillon i.
Variations inconnues et différentes
Lorsque les variances des deux populations sont inconnues et ne peuvent pas être supposées égales, la formule de calcul de l’intervalle de confiance pour la différence des moyennes avec un niveau de confiance de 1-α est la suivante :
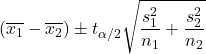
Où:
 est la moyenne de l’échantillon i.
est la moyenne de l’échantillon i.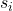 est l’écart type de l’échantillon i.
est l’écart type de l’échantillon i. est la valeur de la distribution t de Student avec une probabilité de α/2.
est la valeur de la distribution t de Student avec une probabilité de α/2. est la taille de l’échantillon i.
est la taille de l’échantillon i.
Dans ce cas, les degrés de liberté de la distribution t de Student sont calculés à l’aide de la formule suivante :

Où
![]() est l’écart type de l’échantillon i.
est l’écart type de l’échantillon i.
Exemple concret de l’intervalle de confiance pour la différence de moyennes
Après avoir vu la définition de l’intervalle de confiance pour la différence de moyennes et quelles sont les différentes formules, nous allons maintenant voir un exemple concret pour finir d’assimiler comment est calculé l’intervalle de confiance pour la différence de deux moyennes.
- Nous souhaitons étudier l’effet du tabac sur le poids des enfants à la naissance. Pour ce faire, deux échantillons sont comparés : le premier échantillon est constitué d’enfants dont les mères ne fumaient pas et le deuxième échantillon est constitué d’enfants dont les mères fumaient (les paramètres de l’échantillon sont indiqués ci-dessous). Calculez l’intervalle de confiance pour la différence de moyennes avec un niveau de confiance de 95 %.
- Mères non fumeuses :
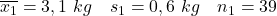
- Mères fumeuses :
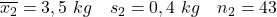
- Mères non fumeuses :
Dans ce cas, nous ne connaissons pas les valeurs des variances de population, cependant, on peut supposer que les variances de population sont équivalentes car nous avons affaire à deux populations ayant des caractéristiques très similaires. Par conséquent, la formule de l’intervalle de confiance pour la différence de moyenne que nous devons utiliser est la suivante :
![]()
Ainsi, nous calculons l’écart type combiné à partir des écarts types des deux échantillons :
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
De même, il faut rechercher la valeur de la distribution t de Student de 80 degrés de liberté avec une probabilité de 2,5% dans le tableau de distribution de probabilité de la distribution t de Student :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Enfin, nous substituons les données dans la formule d’intervalle de confiance pour la différence de moyennes et effectuons les calculs :
![]()
![]()
![]()
L’intervalle de confiance pour la différence des moyennes du problème est donc le suivant :
![]()
