Répartition d’échantillonnage de la différence de proportions
Cet article explique ce qu’est la distribution d’échantillonnage de la différence de proportions et à quoi elle sert dans les statistiques. La formule de répartition d’échantillonnage de la différence de proportions et un exercice résolu étape par étape sont également présentés.
Quelle est la distribution d’échantillonnage de la différence de proportions ?
La distribution d’échantillonnage de la différence de proportions est la distribution qui résulte du calcul des différences entre les proportions d’échantillonnage de tous les échantillons possibles provenant de deux populations différentes.
Autrement dit, le processus permettant d’obtenir la distribution d’échantillonnage de la différence de proportions consiste, premièrement, à extraire tous les échantillons possibles de deux populations différentes, deuxièmement, à déterminer la proportion de chaque échantillon extrait et enfin, à déterminer la différence entre toutes les proportions de la différence de proportions. deux populations. De sorte que l’ensemble des résultats obtenus après avoir effectué ces opérations forme la distribution d’échantillonnage de la différence de proportions.

En statistiques, la distribution d’échantillonnage de la différence de proportions est utilisée pour calculer la probabilité que la différence entre les proportions d’échantillon de deux échantillons sélectionnés au hasard soit proche de la différence des proportions de population.
Formule pour la distribution d’échantillonnage de la différence de proportions
Les échantillons sélectionnés pour la distribution d’échantillonnage de la différence de proportions sont définis par des distributions binomiales , car à des fins pratiques, une proportion est un rapport entre les cas de réussite et le nombre total d’observations.
Néanmoins, en raison du théorème central limite, les distributions binomiales peuvent être approchées des distributions de probabilité normales . Par conséquent, la distribution d’échantillonnage de la différence de proportions peut être approchée d’une distribution normale avec les caractéristiques suivantes :
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
Remarque : La distribution d’échantillonnage de la différence de proportions ne peut être approchée d’une distribution normale que si
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() et
et![]() .
.
Par conséquent, puisque la distribution d’échantillonnage de la différence de proportions peut être approchée d’une distribution normale, la formule pour calculer la statistique de la distribution d’échantillonnage de la différence de proportions est la suivante :

Où:
 est la proportion d’échantillon i.
est la proportion d’échantillon i. est la proportion de population i.
est la proportion de population i. est la probabilité d’échec de la population i,
est la probabilité d’échec de la population i, .
. est la taille de l’échantillon i.
est la taille de l’échantillon i. est une variable définie par la distribution normale standard N(0,1).
est une variable définie par la distribution normale standard N(0,1).
Cette formule est similaire à la formule de test d’hypothèse pour la différence de proportions.
Exemple concret de la distribution d’échantillonnage de la différence de proportions
Après avoir vu la définition de la distribution d’échantillonnage de la différence de proportions et quelle est sa formule, vous pouvez voir ci-dessous un exemple résolu étape par étape pour finir de comprendre le concept.
- Vous souhaitez analyser la précision de deux usines de production, une usine produit de telle manière que seulement 5 % des pièces produites présentent des défauts, tandis que le pourcentage de pièces défectueuses d’une autre usine est de 8 %. Si nous prenons un échantillon de 200 pièces de la première usine et un autre échantillon de 280 pièces de la deuxième usine, quelle est la probabilité que le pourcentage de défauts de la première usine de production soit supérieur au pourcentage de défauts de la deuxième usine ? production?
Pour finir de connaître toutes les données du problème, nous allons d’abord calculer la proportion de parties bien produites de chaque plante :
![Rendered by QuickLaTeX.com \begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7c02732cc5fb319bfa5bf7b8ed8d03db_l3.png)
Si le taux de défauts dans la première usine était supérieur au taux de défauts dans la deuxième usine, cela signifie que l’équation suivante serait vraie :
![]()
Ainsi, pour déterminer la probabilité de distribution d’échantillonnage de la différence de proportions, nous devons appliquer la formule expliquée dans la section ci-dessus :
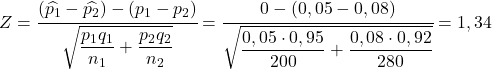
Ainsi, la probabilité que le taux de défauts de la première usine soit supérieur au taux de défauts de la deuxième usine est équivalente à la probabilité que la variable Z soit supérieure à 1,34 :
![]()
Finalement, il suffit de chercher la probabilité correspondante dans le tableau de la distribution normale et nous aurons déjà résolu le problème :
![]()
En bref, la probabilité que la proportion de défauts dans la première usine soit supérieure à la proportion de défauts dans la deuxième usine est de 9,01 %.
