Distribution d’échantillonnage de la moyenne

Cet article explique ce qu’est la distribution d’échantillonnage de la moyenne en statistiques. Vous trouverez également la formule de répartition d’échantillonnage de la moyenne et un exercice résolu étape par étape.

Quelle est la distribution d’échantillonnage de la moyenne ?

La distribution d’échantillonnage de la moyenne (ou distribution d’échantillonnage des moyennes ) est la distribution qui résulte du calcul de la moyenne d’échantillonnage de chaque échantillon possible d’une population. Autrement dit, l’ensemble des moyennes d’ échantillon de tous les échantillons possibles d’une population forme la distribution d’échantillonnage de la moyenne.

Ou en d’autres termes, si nous étudions tous les échantillons pouvant être extraits d’une population et calculons la moyenne de chacun des échantillons, l’ensemble des valeurs calculées forme une distribution d’échantillonnage de la moyenne de l’échantillon.

En statistique, la distribution d’échantillonnage de la moyenne est utilisée pour calculer la probabilité d’approcher la valeur de la moyenne de la population lors de l’analyse d’un seul échantillon.

Formule pour la distribution d’échantillonnage de la moyenne

Étant donné une population qui suit une distribution de probabilité normale de moyenne

et écart type et des échantillons de taille en sont extraits , la distribution d’échantillonnage de la moyenne sera également définie par une distribution normale ayant les caractéristiques suivantes :

Où

est la moyenne de la distribution d’échantillonnage de la moyenne et est son écart type. En outre, est l’erreur type de la distribution d’échantillonnage.

Remarque : si la population ne suit pas une distribution normale mais que la taille de l’échantillon est grande (n>30), la distribution d’échantillonnage de la moyenne peut également être approchée de la distribution normale précédente par le théorème central limite.

Par conséquent, puisque la distribution d’échantillonnage de la moyenne suit une distribution normale, la formule pour calculer toute probabilité liée à la moyenne d’un échantillon est la suivante :

Où:

• est la moyenne de l’échantillon.
• C’est la moyenne de la population.
• est l’écart type de la population.
• est la taille de l’échantillon.
• est une variable définie par la distribution normale standard N(0,1).

Exemple concret de la distribution d’échantillonnage de la moyenne

Après avoir vu la définition de la distribution d’échantillonnage de la moyenne et quelles sont ses formules associées, résolvons un exemple pour mieux comprendre le concept.

• Le poids des étudiants universitaires suit une distribution normale avec une moyenne de 68 kg et un écart type de 9 kg. Déterminer:
  1. Quelle est la probabilité que la moyenne d’un échantillon aléatoire de 25 élèves soit inférieure à 66 kg ?
  2. Si 300 échantillons sont prélevés avec une taille de 25 élèves chacun, combien de moyennes d’échantillons auront une valeur inférieure à 66 kg ?

Tout d’abord, il faut calculer la valeur de la statistique correspondante, pour cela, nous appliquons la formule que nous avons vue ci-dessus :

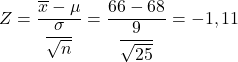
La probabilité que nous recherchons est donc celle correspondant à la valeur Z=-1,11 de la queue gauche de la distribution normale standard, qui peut être facilement obtenue à partir de la table de probabilité Z. Nous utilisons donc la table Z pour déterminer la probabilité que le problème nous demande :

Maintenant que nous connaissons la probabilité que la moyenne d’un échantillon aléatoire soit inférieure à 66 kg, pour connaître le nombre d’échantillons moyens inférieurs à 66 kg en prenant 300 échantillons égaux, nous devons multiplier la probabilité calculée par le nombre total d’échantillons prélevés :

Par conséquent, environ 40 des échantillons extraits auront une moyenne inférieure à 66 kg.