Quasivariance

Cet article explique ce qu’est la quasivariance dans les statistiques. Ainsi, vous découvrirez comment calculer la quasivariance, un exercice résolu et quelles sont les différences entre la quasivariance et la variance. De plus, vous pouvez calculer la quasivariance de n’importe quel ensemble de données avec une calculatrice en ligne.

Qu’est-ce que la quasivariance ?

En statistique, la quasivariance est une mesure de dispersion qui indique la variabilité d’un échantillon. Plus précisément, la quasivariance est égale à la somme des carrés des écarts divisée par le nombre total d’observations moins un.

Le symbole de la quasivariance est

soit . Bien que parfois le symbole soit également utilisé pour représenter la quasivariance.

La quasivariance sert à déterminer la dispersion d’un échantillon tout en évitant les biais, c’est pourquoi elle est souvent appelée variance sans biais. La quasivariance est donc un bon estimateur de la variance de la population. En fait, lors du calcul de la variance de l’échantillon, la formule de quasi-variance est souvent utilisée à la place de la formule de variance. Ci-dessous, nous entrerons en détail sur la différence entre ces deux mesures statistiques.

Formule de quasivariance

Pour calculer la quasivariance, il faut trouver la somme des carrés des différences entre les valeurs et la moyenne de l’ensemble de données et, plus tard, la diviser par le nombre total de données moins un.

Ainsi, la formule pour calculer la quasivariance est la suivante :

Où:

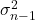• est la quasivariance.
• est la valeur des données .
• est le nombre total de données.
• est la moyenne de l’ensemble de données.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la quasivariance de n’importe quel ensemble de données.

Vous vous demandez peut-être pourquoi il est divisé par n-1 et non par n ? Eh bien, il s’agit d’éliminer le biais, de cette manière on obtient un estimateur sans biais. C’est précisément pourquoi la quasivariance est un bon estimateur de la variance de la population.

Exemple de calcul de quasivariance

Maintenant que nous connaissons la définition de la quasivariance, nous allons résoudre un exemple simple afin que vous puissiez voir comment la quasivariance d’une série de données est calculée.

• D’une entreprise multinationale, on connaît le résultat économique qu’elle a eu au cours des cinq dernières années, dans la plupart elle a obtenu des bénéfices mais une année elle a présenté des pertes considérables : 11,5, 2, -9, 7 millions d’euros. Calculez la quasivariance de cet ensemble de données.

La première chose que nous devons faire pour obtenir la quasivariance d’un ensemble de données est de calculer sa moyenne arithmétique :

Et une fois que l’on connaît la valeur moyenne des données, on applique la formule de quasivariance :

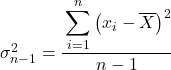
Ainsi, nous substituons les données fournies par l’instruction d’exercice dans la formule :

Finalement, il suffit de résoudre les opérations pour calculer la quasivariance :

Notez que les unités de la quasivariance sont les mêmes unités que les unités des données statistiques mais au carré, donc la quasivariance de cet ensemble de données est de 57,2 millions d’euros ² .

Calculateur de quasivariance

Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer sa quasivariance. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Variance et quasivariance

Enfin, nous verrons la différence entre quasivariance et variance, car malgré leur similitude de nom, elles sont également calculées de manière très similaire.

La différence entre la quasivariance et la variance est le dénominateur de la formule. Pour calculer la quasivariance, vous devez diviser par n-1, cependant, la variance est calculée en divisant par n.

Ainsi, la quasivariance et la variance sont mathématiquement liées, puisque la quasivariance équivaut à la variance multipliée par n (le nombre total de points de données) et divisée par n-1.

Par conséquent, pour le même ensemble de données, la valeur de quasivariance sera toujours supérieure à la valeur de variance.