Distribution exponentielle

Par Pr Amélia Rodriguez août 3, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est la distribution exponentielle dans les statistiques et à quoi elle sert. De même, vous trouverez quelles sont les propriétés de la distribution exponentielle ainsi que ses formules, son graphique et un exercice résolu. De plus, vous pourrez calculer n’importe quelle probabilité avec un calculateur en ligne de distribution exponentielle.

Qu’est-ce que la distribution exponentielle ?

La distribution exponentielle est une distribution de probabilité continue utilisée pour modéliser le temps d’attente pour l’apparition d’un phénomène aléatoire.

Plus précisément, la distribution exponentielle permet de décrire le temps d’attente entre deux événements qui suivent une distribution de Poisson. Par conséquent, la distribution exponentielle est étroitement liée à la distribution de Poisson.

➤ Voir : Qu’est-ce que la distribution de Poisson ?

La distribution exponentielle a un paramètre caractéristique, représenté par la lettre grecque λ et indique le nombre de fois que l’événement étudié est censé se produire au cours d’une période de temps donnée.

$X\sim \text{Exp}(\lambda)$

De même, la distribution exponentielle est également utilisée pour modéliser le temps qui s’écoule jusqu’à ce qu’une panne se produise. La distribution exponentielle a donc plusieurs applications en fiabilité et en théorie de la survie.

Exemples de distributions exponentielles

Maintenant que nous connaissons la définition de la distribution exponentielle, regardons plusieurs exemples de ce type de distribution pour mieux comprendre le concept.

Exemples de distribution exponentielle :

Le temps écoulé entre deux appels dans un centre d’appel.
Le temps qu’une personne doit attendre jusqu’à ce qu’un taxi gratuit passe dans une rue spécifique.
Le temps d’attente jusqu’à ce qu’un nouveau client entre dans un magasin.
Le temps qui s’écoule entre l’entrée de deux utilisateurs différents sur une page Web.
Temps qui s’écoule dans un aéroport entre le décollage d’un avion et le départ d’un autre.

Formule de distribution exponentielle

La formule de la fonction de densité qui définit le calcul d’une probabilité de distribution exponentielle est égale à λ multiplié par le nombre e à la puissance λ négative fois x.

Autrement dit, la formule pour calculer une probabilité de distribution exponentielle est la suivante :

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la probabilité d’une variable qui suit la distribution exponentielle.

D’autre part, la formule pour calculer une probabilité cumulative de la distribution exponentielle est la suivante :

$P[X\leq x]=1-e^{-\lambda x}$

Graphique de distribution exponentielle

Dans cette section, vous pouvez voir la représentation graphique de la fonction de densité et de la fonction de distribution de la distribution exponentielle.

Ci-dessous vous pouvez voir comment le graphique de la fonction densité de la distribution exponentielle varie en fonction de la valeur du paramètre λ.

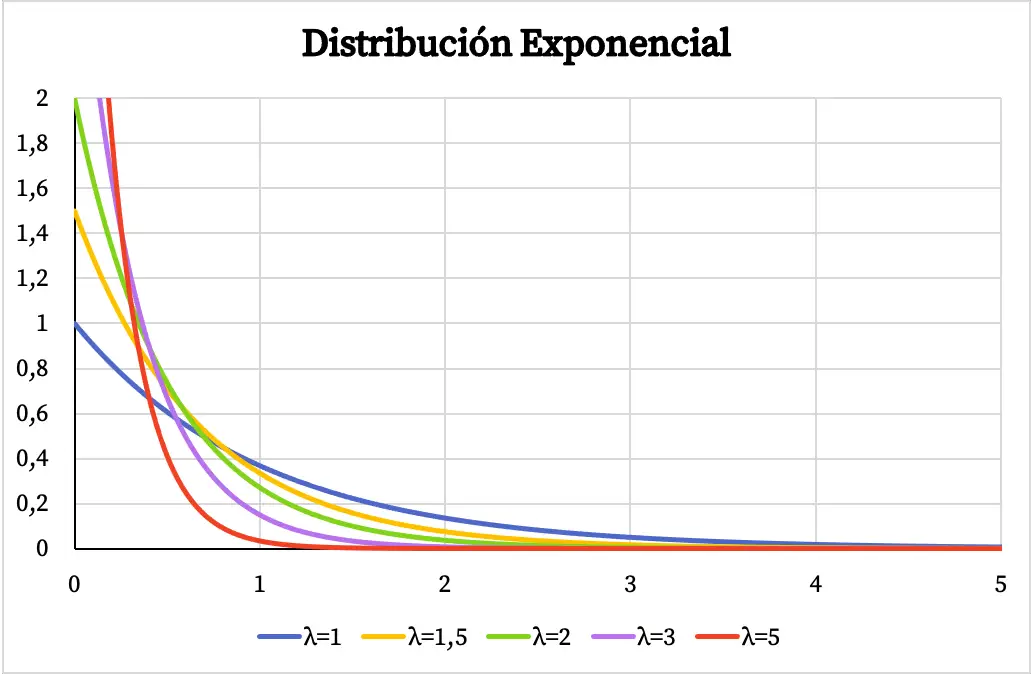
De même, la fonction de probabilité cumulée de la distribution exponentielle dépend également de la valeur du paramètre λ, comme vous pouvez le voir sur le graphique suivant :

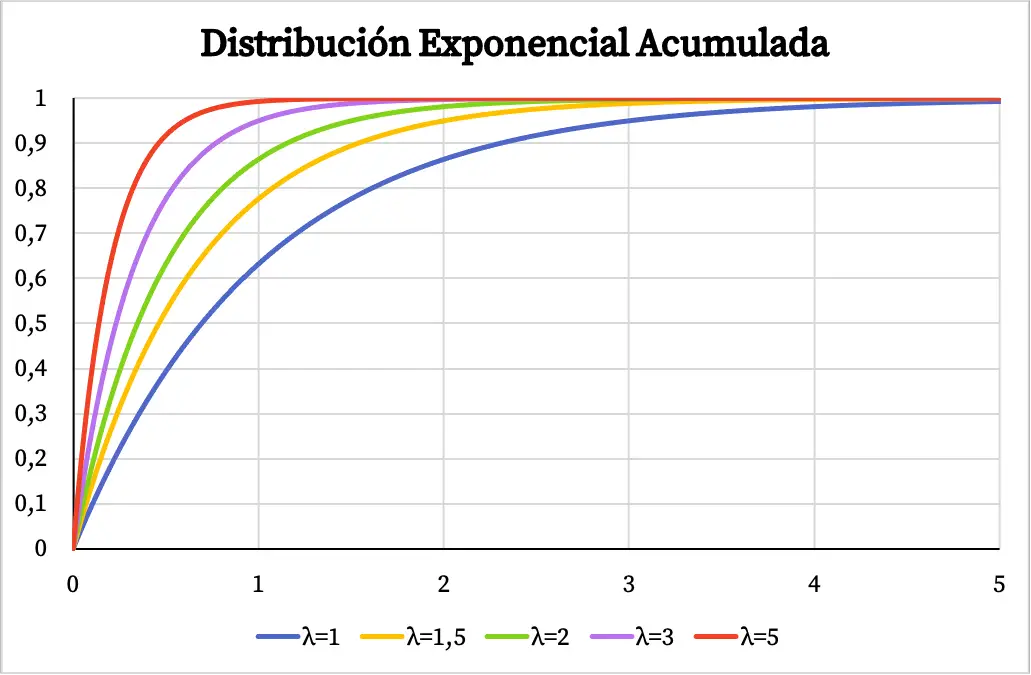
graphique de probabilité cumulée de distribution exponentielle

Exercice résolu sur la distribution exponentielle

En moyenne, λ=1 utilisateurs/min accèdent à une page Web spécifique. Quelle est la probabilité que le temps entre deux utilisateurs entrant soit de 3 minutes ? Et la probabilité que ce soit égal ou inférieur à 2 minutes ?

La distribution qui définit la variable aléatoire de ce problème est une distribution exponentielle, puisque nous étudions le temps qui s’écoule entre le moment où un événement se produit (l’entrée d’un utilisateur sur la page Web) jusqu’à ce que ce même événement se reproduise.

$X\sim \text{Exp}(1)$

Par conséquent, pour calculer la probabilité que le temps écoulé entre l’entrée de deux utilisateurs différents soit de trois minutes, nous devons appliquer la formule de la fonction de densité (voir ci-dessus) :

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

D’autre part, pour déterminer une probabilité cumulée, nous devons utiliser la formule de la fonction de distribution de la distribution exponentielle :

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Caractéristiques de la distribution exponentielle

La distribution exponentielle répond aux caractéristiques suivantes :

La distribution exponentielle a un paramètre caractéristique, λ, qui indique le nombre de fois où le phénomène étudié devrait se produire au cours d’une période de temps donnée.

$X\sim \text{Exp}(\lambda)$

La distribution exponentielle ne peut pas prendre une valeur négative, donc le domaine de la distribution exponentielle est constitué de tous les nombres réels supérieurs ou égaux à zéro.

$x\in [0,+\infty)$

La moyenne de la distribution exponentielle est égale à un divisé par le paramètre caractéristique λ.

$E[X]=\cfrac{1}{\lambda}$

La variance de la distribution exponentielle est le carré de sa moyenne, par conséquent, la variance de la distribution exponentielle est équivalente à un sur le coefficient λ au carré.

$Var(X)=\cfrac{1}{\lambda^2 }$

Quelle que soit la valeur de λ, le coefficient d’asymétrie de la distribution exponentielle est toujours égal à 2.

$A=2$

De même, le coefficient d’aplatissement de toute distribution exponentielle est toujours équivalent à 9.

$C=9$

La formule de la fonction de densité de la distribution exponentielle est la suivante :

$P[X=x]=\lambda e^{-\lambda x}$

Alors que la formule de la fonction de probabilité cumulative de la distribution exponentielle est la suivante :

$P[X\leq x]=1-e^{-\lambda x}$

La distribution exponentielle est l’une des rares distributions de probabilité possédant la propriété de manque de mémoire. Cette propriété signifie que la survenance d’un événement antérieur n’affecte pas la probabilité que cet événement se produise dans le futur. Par exemple, dans une distribution exponentielle, la probabilité qu’un nouvel utilisateur accède à une page Web en moins d’une minute ne dépend pas du fait qu’un utilisateur vient d’entrer ou qu’aucun utilisateur n’y soit entré depuis plus de dix minutes.

$P[X>x+y|X>y]=P[X>x]$

Calculateur de distribution exponentielle

Entrez la valeur du paramètre λ et la valeur de x dans la calculatrice suivante pour calculer la probabilité. Vous devez sélectionner la probabilité que vous souhaitez calculer et saisir les nombres en utilisant le point comme séparateur décimal, par exemple 0,50.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus