Distribution normale standard

Cet article explique ce qu’est la distribution normale standard et à quoi elle sert. Vous trouverez également les propriétés de la distribution normale standard, le tableau avec ses valeurs caractéristiques et, en plus, un exercice résolu.

Quelle est la distribution normale standard ?

La distribution normale standard , également appelée distribution normale unitaire , est le cas le plus simple de distribution normale. Plus précisément, la distribution normale standard est une distribution normale avec des valeurs moyennes et d’écart type égales à 0 et 1 respectivement.

Par conséquent, la distribution normale standard est définie comme N(0,1), où le premier paramètre est la moyenne de la distribution et le deuxième paramètre est son écart type (ou écart type).

Le graphique de la distribution normale standard est donc le suivant :

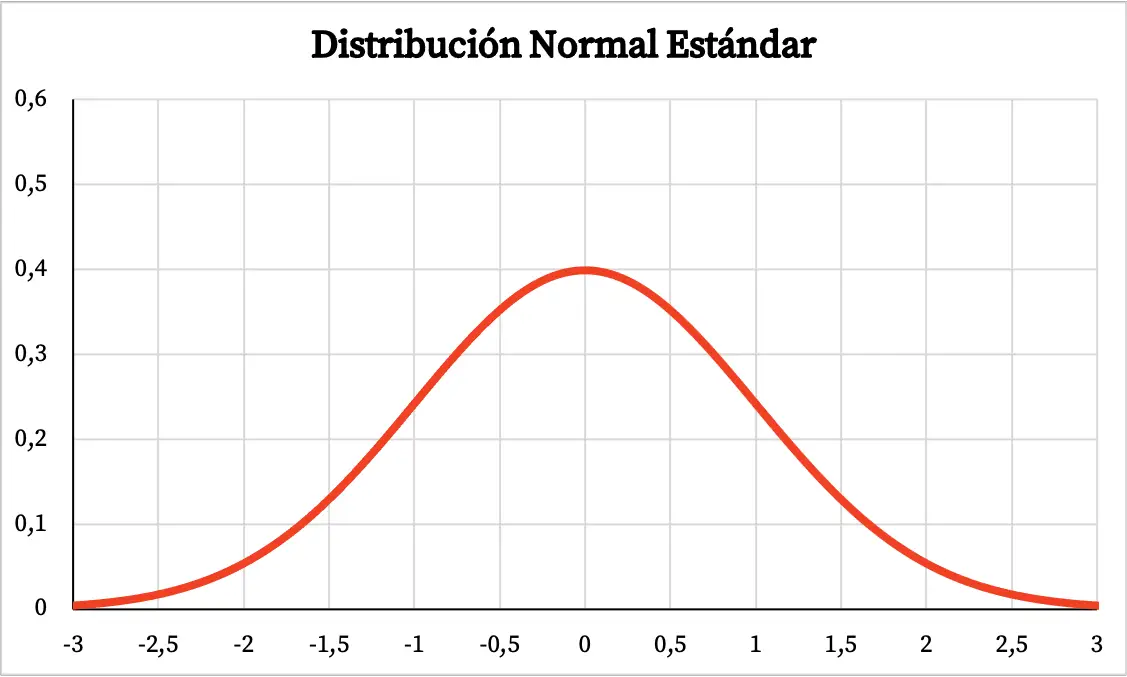
Formule pour la distribution normale standard

Pour transformer toute distribution normale en distribution normale standard, vous devez soustraire la moyenne de la distribution normale de toutes ses valeurs puis diviser par l’écart type de la distribution normale.

La formule de la distribution normale standard est donc la suivante :

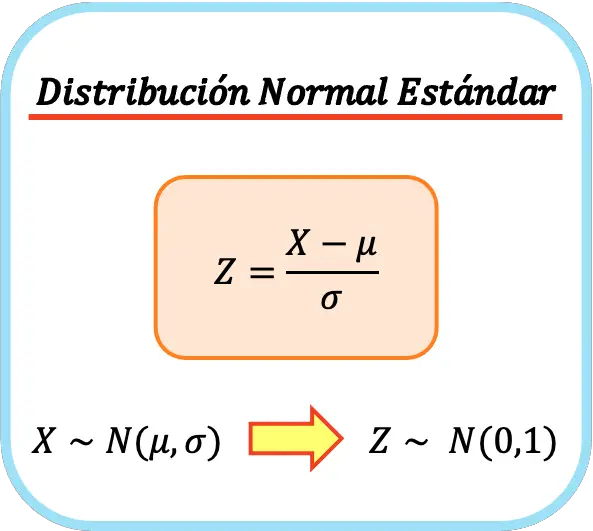
De cette façon, la moyenne arithmétique et l’écart type de la nouvelle variable seront respectivement 0 et 1, nous obtiendrons donc une distribution normale standard. Ce processus est également appelé normalisation à une variable ou normalisation à une variable .

Tableau de distribution normale standard

Le tableau d’une distribution normale standard est un tableau qui contient les probabilités qu’une valeur observée soit inférieure à une valeur donnée de la distribution normale standard.

De plus, puisque la fonction d’une distribution normale dépend de sa moyenne et de son écart type, le tableau de distribution normale standard est également utilisé, par extension, pour déterminer les probabilités de toute distribution normale. Pour ce faire, la distribution normale est typée en une distribution normale standard puis nous regardons dans le tableau quelle probabilité lui correspond.

Ainsi, les valeurs du tableau de la distribution normale standard sont les suivantes :

Exemple de distribution normale standard

Maintenant que nous connaissons la définition de la distribution normale standard et quelle est sa formule, vous trouverez ci-dessous un exemple concret pour bien comprendre le concept.

• Une variable aléatoire continue suit une loi normale de moyenne 45 et d’écart type 15, quelle est la probabilité d’obtenir une valeur inférieure ou égale à 58 ?

Pour trouver la probabilité d’une distribution normale, nous devons utiliser son tableau de caractéristiques, mais pour ce faire, nous devons d’abord effectuer le processus de typage pour obtenir la distribution normale standard. Nous utilisons donc la formule de la distribution normale standard :

Nous soustrayons donc la moyenne de la valeur de probabilité, puis divisons par l’écart type

Une fois que nous avons standardisé la variable, nous allons au tableau de probabilité de la distribution normale standard (voir ci-dessus) pour voir à quelle probabilité correspond la valeur de 0,87 :

La probabilité d’obtenir une valeur égale ou inférieure à 58 est donc de 80,78 %.

Caractéristiques de la distribution normale standard

La distribution normale standard a les caractéristiques suivantes :

• La distribution normale standard est une distribution symétrique centrée sur 0.
• Comme une distribution normale, le graphique de la distribution normale standard est en forme de cloche, la majeure partie de la zone du graphique se situant autour de la moyenne.
• Par conséquent, la moyenne, le mode et la médiane d’une distribution normale ont la même valeur, qui est 0.
• La distribution normale standard a un maximum à z=0.
• De même, la distribution normale standard a deux points d’inflexion, à z=-1 et z=+1.
• D’après la règle empirique, on sait que 68% des valeurs se situent dans une distribution normale standard entre +1 et -1, 95% des valeurs entre +2 et -2 et 99,7% des valeurs entre +3 et -3.