Snedecor F Distribution

Par Pr Amélia Rodriguez août 4, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est la distribution Snedecor F et à quoi elle sert. De plus, vous pourrez voir le graphique de la distribution Snedecor F et quelles sont ses propriétés statistiques.

Quelle est la distribution Snedecor F ?

La distribution F de Snedecor , également appelée distribution F de Fisher – Snedecor ou simplement distribution F , est une distribution de probabilité continue utilisée dans l’inférence statistique, en particulier dans l’analyse de la variance.

L’une des propriétés de la distribution Snedecor F est qu’elle est définie par la valeur de deux paramètres réels, m et n , qui indiquent leurs degrés de liberté. Ainsi, le symbole de la distribution Snedecor F est F _m,n , où m et n sont les paramètres qui définissent la distribution.

$F_{m,n}\qquad m,n>0$

Mathématiquement, la distribution Snedecor F est égale au quotient entre une distribution du chi carré et ses degrés de liberté divisé par le quotient entre une autre distribution du chi carré et ses degrés de liberté. Ainsi, la formule qui définit la distribution Snedecor F est la suivante :

$\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}$

➤ Voir : Quelle est la distribution du chi carré ?

La distribution Fisher-Snedecor F doit son nom au statisticien anglais Ronald Fisher et au statisticien américain George Snedecor.

En statistique, la distribution Fisher-Snedecor F a différentes applications. Par exemple, la distribution F de Fisher-Snedecor est utilisée pour comparer différents modèles de régression linéaire, et cette distribution de probabilité est utilisée dans l’analyse de variance (ANOVA).

Diagramme de distribution Snedecor F

Une fois que nous avons vu la définition de la distribution Snedecor F, le graphique de sa fonction de densité et le graphique de sa probabilité cumulée sont présentés ci-dessous.

Dans le graphique ci-dessous, vous pouvez voir plusieurs exemples de distributions Snedecor F avec différents degrés de liberté.

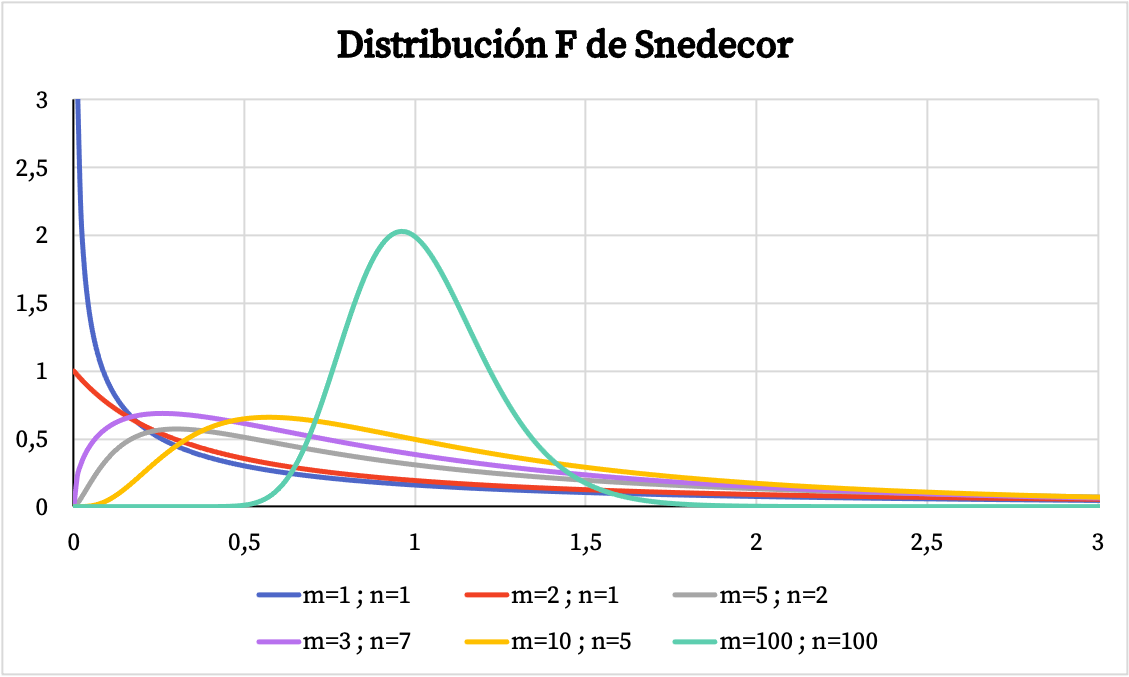
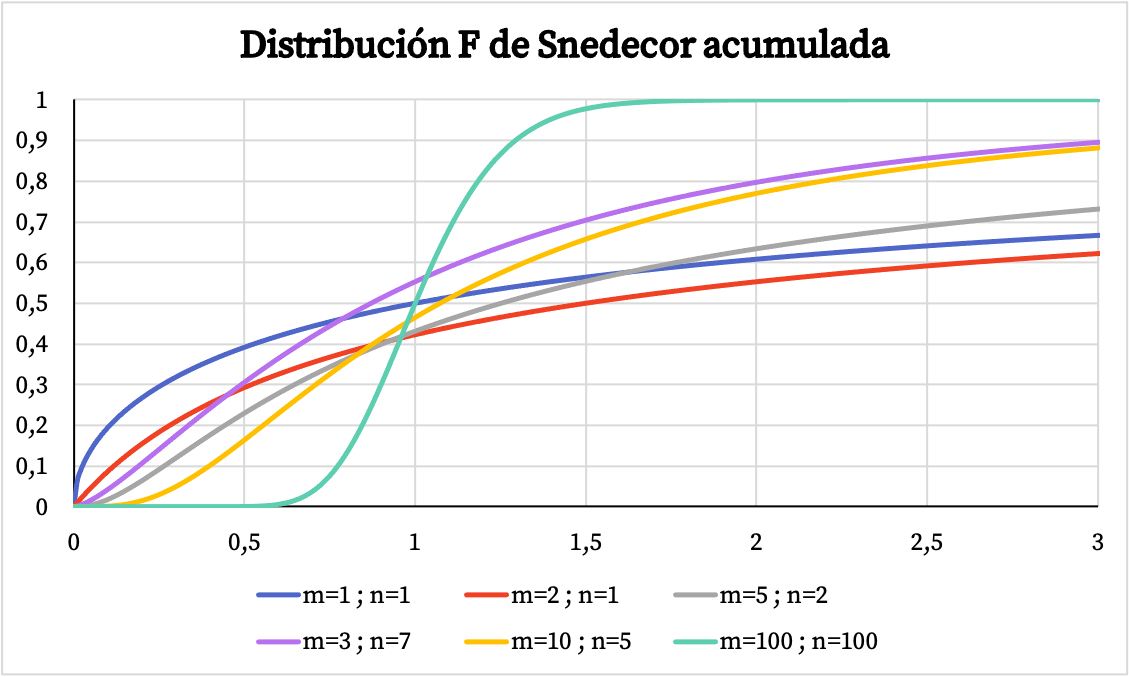
D’autre part, dans le graphique ci-dessous, vous pouvez voir comment le graphique de la fonction de probabilité cumulée de la distribution Snedecor F varie en fonction de ses valeurs caractéristiques.

probabilité cumulée de la distribution Snedecor F

Caractéristiques de la distribution Snedecor F

Enfin, cette section présente les caractéristiques les plus importantes de la distribution Snedecor F.

Les degrés de liberté de la distribution Snedecor F, m et n , sont deux paramètres qui définissent la forme de la distribution. Ces valeurs caractéristiques de la distribution Snedecor F sont des entiers positifs.

$\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}$

Le domaine de la distribution Snedecor F est constitué de tous les nombres réels supérieurs ou égaux à zéro.

$x\in [0,+\infty)$

Pour les valeurs de n supérieures à 2, la moyenne de la distribution Snedecor F est égale à n sur la soustraction de n moins 2.

$\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array}$

Lorsque le paramètre n est supérieur à 2, la variance de la distribution Snedecor F peut être calculée en appliquant la formule suivante :

$\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array}$

Si le paramètre m est supérieur à 2, le mode de la distribution Snedecor F peut être calculé avec l’expression suivante :

$Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2$

La formule de la fonction de densité de la distribution Snedecor F est la suivante :

$\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}$

Si une variable suit une distribution Snedecor F avec des degrés de liberté m et n , alors l’inverse de ladite variable suit une distribution Snedecor F avec les mêmes degrés de liberté mais en changeant l’ordre de ses valeurs.

$X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}$

La distribution Student t a la relation suivante avec la distribution Snedecor F :

$X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}$

➤ Voir : Qu’est-ce que la distribution t de Student ?

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus