Fréquence relative cumulée

Cet article explique en quoi consiste la fréquence relative cumulée dans les statistiques. Ainsi, vous trouverez la définition de la fréquence relative cumulée, comment obtenir la fréquence relative cumulée et deux exercices résolus étape par étape.

Qu’est-ce que la fréquence relative cumulée ?

En statistiques, la fréquence relative cumulée est la somme cumulée des fréquences relatives. Autrement dit, la fréquence relative cumulée d’une valeur est égale à la fréquence relative de cette valeur plus les fréquences relatives de toutes les valeurs inférieures à elle.

Le symbole de la fréquence relative cumulée est H _i . Cependant, dans les statistiques, il n’existe pas encore de consensus complet concernant le symbole de ce type de fréquence, c’est pourquoi vous pouvez également le trouver exprimé à l’aide d’un autre symbole.

Évidemment, pour comprendre la signification de la fréquence relative cumulée, vous devez d’abord être clair sur le concept de fréquence relative, c’est pourquoi je vous recommande de visiter le lien suivant avant de poursuivre l’explication :

Comment calculer la fréquence relative cumulée

Pour calculer la fréquence relative cumulée, les étapes suivantes doivent être suivies :

1. Construisez un tableau de fréquence avec toutes les différentes valeurs de l’échantillon statistique.
2. Calculez la fréquence absolue de chaque valeur.
3. À partir des fréquences absolues, déterminez la fréquence relative de chaque valeur.
4. Trouvez la fréquence relative cumulée de chaque valeur, qui est calculée en ajoutant la fréquence relative de la valeur elle-même plus les fréquences relatives de toutes les valeurs plus petites.

Gardez à l’esprit que si vous souhaitez calculer le pourcentage de fréquence relative cumulée , c’est-à-dire la fréquence relative cumulée exprimée en pourcentage, il vous suffit de suivre les mêmes étapes et de multiplier les résultats par 100.

Exemples de fréquence relative cumulative

Afin que vous puissiez voir comment la fréquence relative cumulée est calculée, deux exemples résolus étape par étape sont présentés ci-dessous. Dans le premier exemple, on trouve la fréquence relative cumulée d’une variable discrète et dans le deuxième exemple, une variable continue, puisque le processus varie légèrement.

Exemple 1 : variable discrète

• Les notes obtenues dans la matière statistique dans une classe de 30 étudiants sont les suivantes. Quelle est la fréquence relative cumulée de chaque note ?

Dans ce cas, la variable est discrète, puisqu’elle ne peut pas prendre de valeur décimale. Il n’est donc pas nécessaire de regrouper les données par intervalles, mais on peut faire les calculs directement.

Ainsi, nous dressons un tableau de fréquences et déterminons la fréquence absolue de chaque valeur différente :

Ensuite, nous calculons la fréquence relative de chaque valeur (vous pouvez voir comment cela se fait dans le lien au début du post).

Et une fois que nous avons calculé la fréquence absolue et la fréquence relative de l’ensemble de données, nous pouvons obtenir la fréquence relative cumulée. Pour ce faire, il faut additionner la fréquence relative de la valeur en question plus toutes les fréquences relatives précédentes ou, en d’autres termes, la fréquence relative accumulée précédente :

En bref, le tableau des fréquences avec la fréquence absolue, la fréquence relative et la fréquence relative cumulée est le suivant :

Gardez à l’esprit que la dernière valeur de la fréquence relative cumulée doit toujours être 1. Si vous obtenez un autre nombre, cela signifie que vous avez commis une erreur dans les calculs.

Exemple 2 : variable continue

• La taille de 20 personnes a été mesurée et les résultats notés ci-dessous ont été obtenus. Séparez les données en intervalles et trouvez la fréquence relative cumulée de chaque intervalle.

Ce cas est différent du problème précédent puisque les nombres sont décimaux, ce qui signifie que la variable peut prendre n’importe quelle valeur et est donc continue. Nous allons donc réaliser le tableau des fréquences en regroupant les données en intervalles.

Nous construisons donc le tableau et obtenons la fréquence absolue de chaque intervalle :

Nous calculons maintenant les fréquences relatives en divisant la fréquence absolue de chaque intervalle par le nombre total de données :

Et enfin, on trouve les fréquences relatives cumulées de tous les intervalles. Comme précédemment, pour déterminer une fréquence relative cumulée d’un intervalle il faut additionner la fréquence relative dudit intervalle plus les fréquences relatives précédentes :

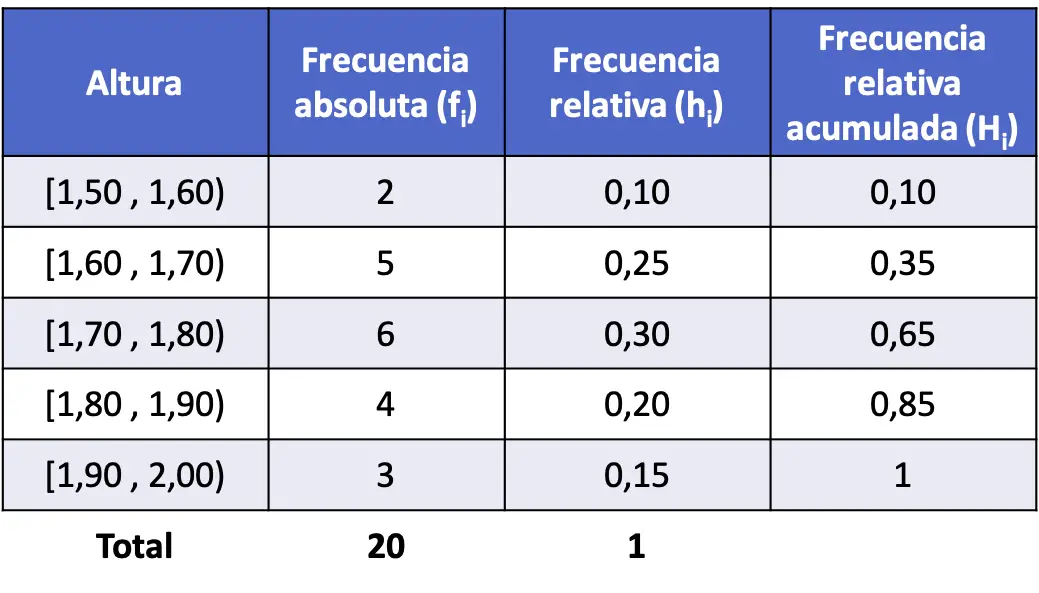
Fréquence relative cumulée et fréquence absolue cumulée

Nous venons de voir comment la fréquence relative cumulée est dérivée de la fréquence relative. Cependant, ce type de fréquence peut également être trouvé en utilisant la fréquence absolue cumulée.

La fréquence relative cumulée peut être calculée en divisant la fréquence absolue cumulée par le nombre total de données dans l’échantillon.

Par conséquent, la formule de la fréquence relative cumulée est la suivante :

Où:

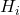• est la fréquence relative cumulée.
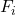• est la fréquence absolue accumulée .
• est le nombre total de données.

Suivant le premier exemple élaboré ci-dessus, voici comment la fréquence relative accumulée est trouvée à partir de la fréquence absolue accumulée :

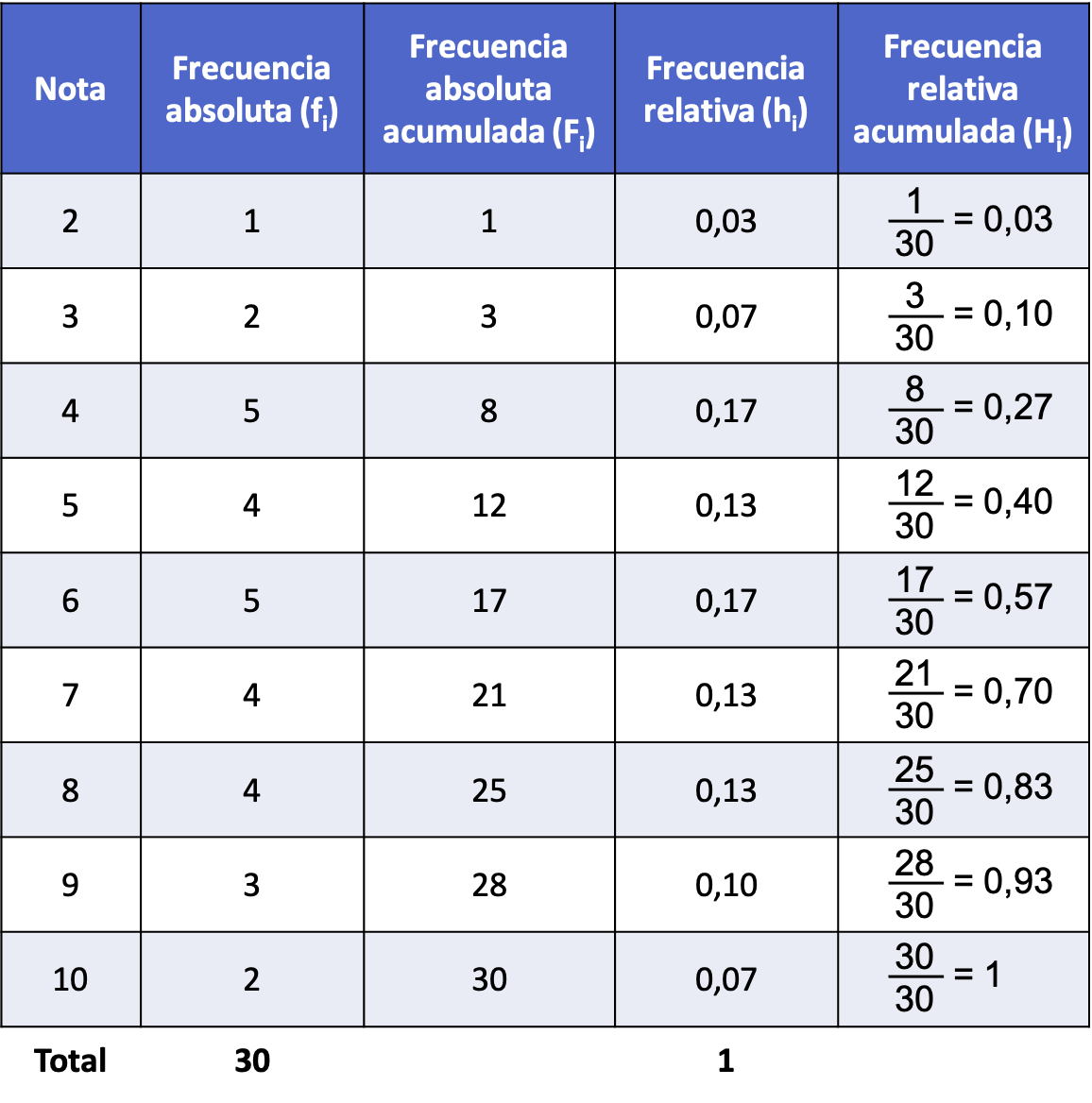
Le tableau ci-dessus, puisqu’il contient tous les types de fréquences statistiques, est appelé tableau des fréquences. Cliquez ici pour en savoir plus :