Fréquence relative

Dans cet article, vous découvrirez ce qu’est la fréquence relative dans les statistiques, comment obtenir la fréquence relative et deux exercices résolus étape par étape sur la fréquence relative.

Qu’est-ce que la fréquence relative ?

En statistiques, la fréquence relative est une mesure qui indique le nombre de fois qu’une valeur apparaît dans un échantillon de données sous la forme d’une proportion ou d’un pourcentage. Plus précisément, la fréquence relative est égale à la fréquence absolue divisée par le nombre total de données.

Par exemple, si la fréquence absolue d’une valeur est de 15 et qu’il existe 100 points de données au total, la fréquence relative de cette valeur est de 0,15 (15/100=0,15).

En général, le symbole h _i est utilisé pour représenter la fréquence relative. Bien qu’il n’y ait toujours pas de consensus dans la communauté statistique, vous pouvez donc voir la fréquence relative représentée par un autre symbole.

Comment calculer la fréquence relative

La fréquence relative est égale à la fréquence absolue divisée par le nombre total de données. Par conséquent, pour calculer la fréquence relative, vous devez d’abord trouver la fréquence absolue, puis la diviser par le nombre total d’observations.

Ainsi, la formule de fréquence relative est la suivante :

Où:

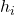• est la fréquence relative.
• est la fréquence absolue.
• est le nombre total de données.

En revanche, pour calculer la fréquence relative en pourcentage , c’est-à-dire la fréquence relative exprimée en pourcentage, il suffit de multiplier la formule précédente par 100 :

Exemples de fréquence relative

Une fois que vous avez vu la définition de la fréquence relative, vous trouverez ci-dessous deux exemples concrets afin que vous puissiez voir comment ce type de fréquence est calculé. Dans le premier exemple, la fréquence relative d’une variable discrète est déterminée et dans le deuxième exemple, une variable continue.

Exemple 1 : variable discrète

• Les notes obtenues dans la matière statistique dans une classe de 30 étudiants sont les suivantes. Quelle est la fréquence relative de chaque note ?

La variable dans cet exercice est discrète car les données ne peuvent être que des nombres entiers ; par conséquent, il n’est pas nécessaire de regrouper les données en intervalles.

Afin de trouver la fréquence relative, il faut d’abord déterminer la fréquence absolue. Nous construisons donc un tableau de fréquences et calculons la fréquence absolue pour chaque valeur différente :

Maintenant que nous avons calculé la fréquence absolue, nous pouvons calculer la fréquence relative. Pour ce faire il suffit de diviser chaque fréquence absolue par le nombre total de données (30) :

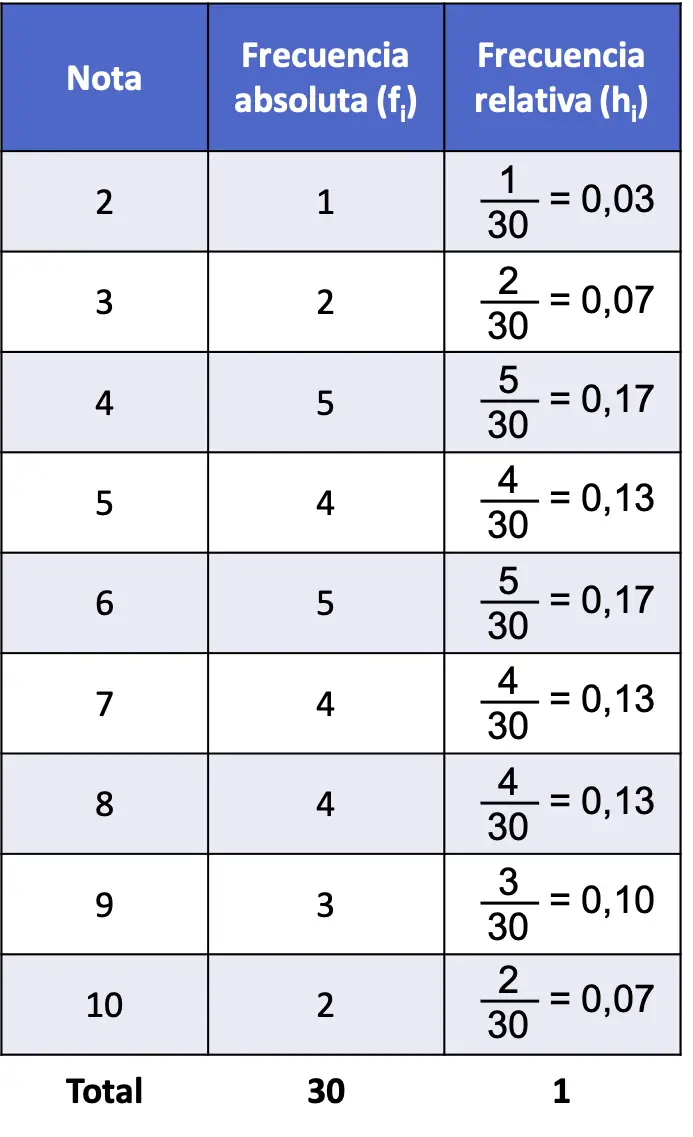
Ainsi, le tableau des fréquences du problème avec la fréquence absolue et la fréquence relative est le suivant :

Notez que la somme de toutes les fréquences relatives donne toujours 1, sinon cela signifie que certains calculs sont erronés.

Exemple 2 : variable continue

• La taille de 20 personnes a été mesurée et les résultats notés ci-dessous ont été obtenus. Séparez les données en intervalles et trouvez la fréquence relative de chaque intervalle.

Les données de cet échantillon statistique appartiennent à une variable continue, puisqu’elles sont décimales et donc la variable peut prendre n’importe quelle valeur. Ainsi avant de faire les calculs de fréquence, nous allons d’abord regrouper les données en intervalles d’une amplitude de 10 dixièmes.

Ensuite, nous faisons un tableau de fréquences avec la fréquence absolue de chaque intervalle :

Et une fois que nous avons trouvé la fréquence absolue, nous pouvons obtenir la fréquence relative de chaque intervalle en divisant sa fréquence absolue par le nombre total de données (20) :

Fréquence relative cumulée

Comme son nom l’indique, la fréquence relative cumulée est un autre type de fréquence utilisé dans les statistiques et calculée à partir de la fréquence relative.

Plus précisément, la fréquence relative cumulée d’une valeur est égale à la somme de la fréquence relative de la valeur elle-même plus les fréquences relatives de toutes les valeurs plus petites.

Afin que vous puissiez voir comment la fréquence relative cumulée est obtenue, la fréquence relative cumulée de l’ensemble de données dans le premier exemple a été calculée ci-dessous :