Diagramme de tige et de feuille

Cet article explique ce que sont les diagrammes de tiges et de feuilles dans les statistiques et à quoi ils servent. Vous découvrirez donc comment construire un diagramme tiges-feuilles, des exercices résolus pour ce type de graphiques statistiques et, enfin, quels sont les avantages et les inconvénients du diagramme tiges-feuilles.

Qu’est-ce que le diagramme tiges-feuilles ?

Le diagramme à tiges et à feuilles est un type de diagramme statistique dans lequel un ensemble de données quantitatives est représenté.

Dans un diagramme tige-feuille, chaque point de données est séparé par la feuille , qui est son dernier chiffre, et la tige , qui sont les chiffres restants. Ainsi, dans un diagramme tige-feuille, chaque feuille est placée sur la ligne de sa tige correspondante.

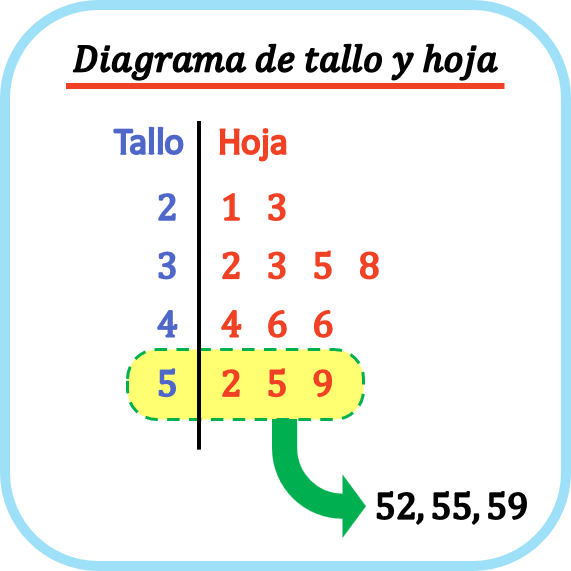
De cette manière, les diagrammes à tiges et à feuilles permettent de représenter graphiquement un ensemble de données statistiques et aident également à visualiser la forme de la distribution.

Le diagramme de tiges et de feuilles est également connu sous le nom de diagramme de tiges et de feuilles , un nom qui vient de l’anglais.

Le tracé des tiges et des feuilles est très similaire à l’ histogramme , bien que cet autre type de graphique statistique soit utilisé pour des échantillons de plus grande taille.

Comment faire un diagramme de tiges et de feuilles

Pour créer un diagramme de tiges et de feuilles, suivez ces étapes :

1. Triez les données de la plus petite à la plus grande.
2. Si nécessaire, arrondissez les nombres jusqu’à ce qu’ils aient le nombre de chiffres souhaité.
3. Décidez dans quel chiffre la coupe sera faite entre la tige et la feuille, c’est-à-dire déterminez le nombre de chiffres que comporteront les feuilles. En règle générale, la feuille est conçue pour contenir uniquement le dernier chiffre de chaque élément de données.
4. Représentez chaque donnée dans le diagramme de tige et de feuille. Les tiges sont placées dans la colonne de gauche par ordre croissant, tandis que les feuilles sont placées dans la colonne de droite à la hauteur de leur tige correspondante et également par ordre croissant.

Exemple de tracé de tiges et de feuilles

Afin que vous puissiez voir comment créer un diagramme de tiges et de feuilles, nous résolvons deux exemples ci-dessous : un sans décimales et un autre avec des décimales.

Exemple 1

• Représentez la série de données suivante dans un diagramme de tiges et de feuilles :

Dans ce cas les données sont déjà ordonnées et arrondies, il n’est donc pas nécessaire d’effectuer ces deux étapes. Ainsi, puisque les nombres ont deux chiffres, ils seront représentés de telle sorte que les dizaines soient la tige et les unités les feuilles du graphique.

Nous allons d’abord représenter la tige du diagramme. Les dizaines des données vont jusqu’à 9, nous faisons donc une ligne pour chaque dizaine :

Et puis on représente les feuilles, pour cela, on place l’unité de chaque donnée dans sa ligne correspondante. Par exemple, le nombre 57 ira à la racine 5 et dans la colonne de droite nous ajouterons un 7.

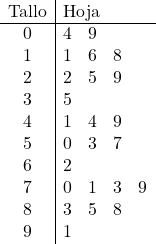
Et de cette manière, toutes les données de l’échantillon ont été représentées dans un diagramme à tiges et à feuilles.

Exemple 2

• Comparez les deux échantillons de données suivants avec des décimales à l’aide d’un diagramme à tiges et feuilles.

Comme vous le verrez dans cet exercice, un seul diagramme à tiges et feuilles peut être utilisé pour représenter deux échantillons statistiques. Par conséquent, nous allons tracer les deux ensembles de données sur le même diagramme à tiges et feuilles : un à gauche et un à droite. Ce type de parcelle est appelé parcelle à tiges et feuilles à double tige .

Dans ce cas, nous prendrons la partie entière des nombres comme tige du diagramme et, par contre, les décimales seront les feuilles du diagramme. Nous construisons donc le tracé à tiges et feuilles en plaçant toutes les parties entières :

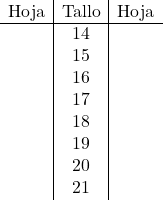
Et maintenant on place la feuille de chaque donnée dans la tige qui lui correspond :

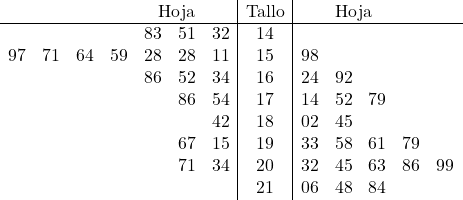
En représentant les données graphiquement, nous pouvons facilement les comparer. Plus précisément, nous voyons que les données de l’échantillon de droite sont un peu plus grandes que celles de gauche, par conséquent, leur moyenne sera également plus grande. Ainsi, selon l’objectif de l’étude statistique, nous serons intéressés à choisir tel ou tel échantillon.

Gardez à l’esprit que vous devez non seulement savoir comment construire un diagramme à barres obliques et à lames, mais vous devez également savoir comment interpréter le graphique.

Avantages et inconvénients de la parcelle à tiges et à feuilles

En raison des caractéristiques de la parcelle à tiges et à feuilles, ces types de parcelles présentent les avantages et les inconvénients suivants :

Avantage:

• Le tracé des tiges et des feuilles vous permet de voir la forme d’une distribution.
• Deux distributions peuvent être comparées à l’aide du diagramme à tiges et feuilles à double tige.
• Il vous permet d’identifier rapidement les valeurs aberrantes dans un ensemble de données.
• Vous pouvez déterminer le mode de la série de données à l’œil nu.

Désavantages:

• Le diagramme à tiges et à feuilles est de moins en moins utilisé, car les logiciels informatiques peuvent rapidement créer un graphique plus complexe.
• La taille de l’échantillon à représenter est limitée, généralement entre 15 et 150 données.
• Seules les données quantitatives peuvent être représentées.