Règle de Sturges
Cet article explique ce qu’est la règle de Sturges et quelle est sa formule. Vous trouverez également un exemple concret étape par étape de la règle de Sturges et, en plus, un calculateur de règle de Sturges en ligne.
Quelle est la règle de Sturges ?
La règle de Sturges est une règle utilisée pour calculer le nombre idéal de classes ou d’intervalles dans lesquels un ensemble de données doit être divisé.
La formule de la règle de Sturges indique que le nombre de classes est égal à un plus le logarithme en base deux du nombre total de données.
Où
est le nombre de classes ou d’intervalles et
est le nombre total d’observations dans l’échantillon.
La plupart des calculatrices autorisent uniquement les calculs avec des logarithmes en base 10. Dans ce cas, vous pouvez utiliser cette formule équivalente :
La règle de Sturges a été créée en 1926 par le statisticien allemand Herbert Sturges.
Exemple de règle de Sturges
Maintenant que nous savons en quoi consiste la règle de Sturges, nous allons voir en résolvant un exercice étape par étape comment les intervalles d’un ensemble de données sont calculés à l’aide de la règle de Sturges en statistique.
- La taille d’un échantillon de 50 personnes différentes a été mesurée et toutes les valeurs ont été enregistrées dans le tableau de données suivant. Appliquez la règle de Sturges pour diviser l’ensemble de données en intervalles, puis tracez les données sur un histogramme.
Tout d’abord, nous devons séparer les données en intervalles. Au total, il y a 50 éléments de données, nous utilisons donc la règle de Sturges avec cette valeur :
![\begin{array}{l}c=1+\log_2(N)\\[2ex]c=1+\log_2(50)\\[2ex]c=1+5,64\\[2ex]c=6,64\\[2ex]c\approx 7\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9929b0c8f1f7cdf5a6160c07e0205c46_l3.svg "Rendered by QuickLaTeX.com")
Il faut donc séparer les données et les regrouper en sept intervalles. Il nous faut maintenant connaître la largeur de chaque intervalle, pour cela, il suffit de diviser la valeur maximale moins la valeur minimale par le nombre total d’intervalles :
En bref, il doit y avoir 7 intervalles d’une amplitude de 9, donc les intervalles calculés selon la méthode Sturges sont :
Une fois que nous avons calculé les intervalles, nous devons compter le nombre de fois qu’une donnée apparaît dans chaque intervalle et construire le tableau des fréquences :
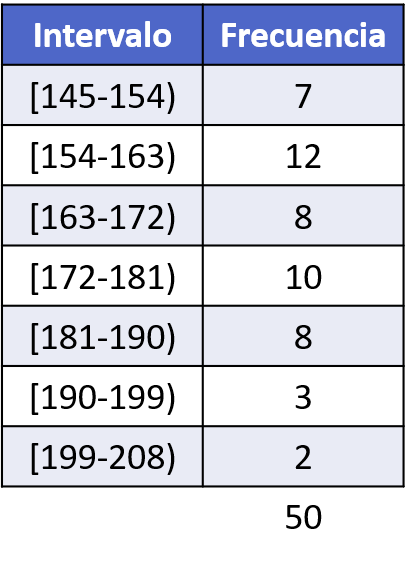
Enfin, à partir du tableau de fréquences, nous pouvons créer l’histogramme pour représenter graphiquement les données :
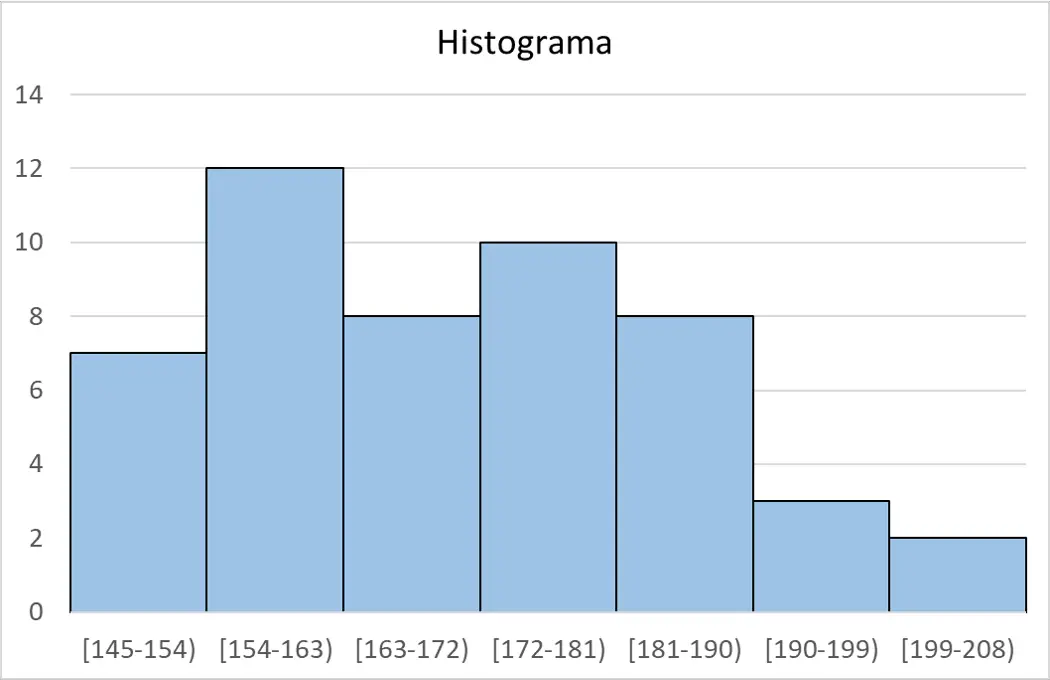
Calculateur de règle de Sturges
Entrez le nombre total d’échantillons de données et cliquez sur « Calculer », puis la calculatrice renverra le nombre d’intervalles calculés selon la règle de Sturges.
à propos de l'auteur
Pr Amélia Rodriguez
En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus