Fonction de répartition

Dans cet article, vous trouverez l’explication de la fonction de distribution, la façon dont ses valeurs sont calculées et un exemple concret de la fonction de distribution. De plus, vous pourrez voir les différences entre une fonction de distribution et une fonction de densité.

Quelle est la fonction de répartition ?

La fonction de distribution , également appelée fonction de distribution cumulative , est une fonction mathématique qui indique la probabilité cumulée d’une distribution. Autrement dit, l’image de la fonction de distribution pour toute valeur est égale à la probabilité que la variable prenne cette valeur ou une valeur inférieure.

La fonction de distribution cumulative peut également être désignée par l’acronyme FDA, bien que son symbole habituel soit le F majuscule.

La fonction de distribution est donc définie par la formule suivante :

Comment calculer la fonction de distribution

Nous expliquons ensuite comment calculer la valeur de la fonction de distribution selon que la distribution de probabilité est discrète ou continue.

Étui discret

Si la variable aléatoire est discrète, la fonction de distribution cumulative est égale à la somme des probabilités de toutes les valeurs égales ou inférieures à x .

Où

est la fonction de probabilité associée à la variable discrète.

Cas continu

Si la variable aléatoire est continue, la fonction de distribution cumulée équivaut à l’intégrale de la fonction de densité de moins l’infini jusqu’à la valeur en question.

Où

est la fonction de densité associée à la variable continue.

Exemple de fonction de distribution

Maintenant que nous connaissons la définition de la fonction de distribution, regardons un exemple pratique étape par étape pour apprendre à calculer une valeur de la fonction de distribution.

• Calculez la fonction de distribution de l’expérience aléatoire consistant à lancer une pièce quatre fois.

Pour résoudre l’exercice, il faut d’abord calculer toutes les probabilités associées au nombre de faces obtenu lors des quatre tirages à pile ou face :

Ainsi, puisqu’il s’agit d’une variable discrète, pour déterminer les images de la fonction de distribution il suffit d’additionner les probabilités jusqu’à la valeur de la variable en question :

Ainsi, les valeurs de la fonction de distribution du retournement des têtes en lançant quatre pièces indépendantes sont les suivantes :

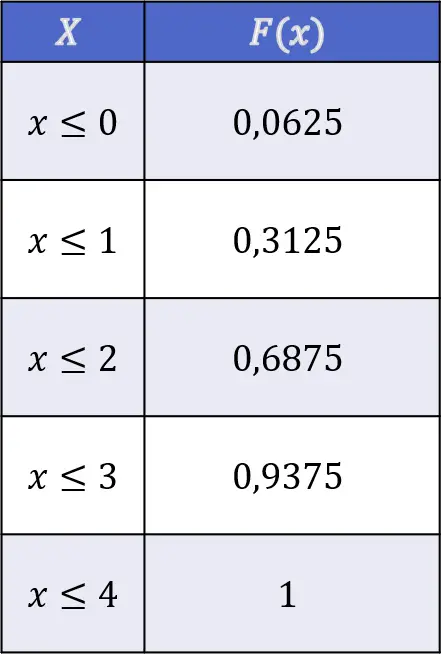
Propriétés de la fonction de distribution

Quel que soit le type de variable, la fonction de distribution a toujours les propriétés suivantes :

• La valeur de la fonction de distribution cumulée est comprise entre 0 et 1 inclus.

• La limite d’une fonction de distribution lorsque x tend vers l’infini est égale à 1.

• D’un autre côté, la limite d’une fonction de distribution lorsque x s’approche de moins l’infini est nulle.

• De par ses caractéristiques, la fonction de distribution est monotone non décroissante.

• De plus, si 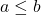les équations suivantes sont satisfaites.

*** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a)=1-F(a^-)\\[2ex]P(a<ul><li> Enfin, si la variable statistique est continue, l'égalité suivante est satisfaite : </li></ul>[latex]\begin{array}{l}P(a \le X \le b) = P(a \le X < b) = P(a < X \le b)=\\[2ex] = P(a < X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... la variable statistique est continue, l'é
Please use \mathaccent for accents in math mode.
leading text: ...iable statistique est continue, l'égalité
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Fonction de distribution et fonction de densité

Enfin, nous verrons quelle est la différence entre la fonction de distribution et la fonction de densité, puisque ces deux notions statistiques sont souvent confondues.

La différence entre la fonction de distribution et la fonction de densité réside dans le type de probabilité qu’elles définissent. La fonction de densité décrit la probabilité que la variable prenne une certaine valeur, tandis que la fonction de distribution décrit la probabilité cumulée de la variable.

Autrement dit, la fonction de distribution est utilisée pour calculer la probabilité que la variable soit égale ou inférieure à une certaine valeur.

Notez que la fonction de densité ne fait référence qu’à des variables continues, cette distinction n’a donc de sens que si la variable étudiée est continue.

Remarquez comment la représentation graphique de la fonction de distribution change par rapport à la fonction de densité d’une variable qui suit une distribution normale avec une moyenne de 1 et un écart type de 0,5 :

Pour en savoir plus sur la fonction de densité, consultez l’article suivant :