Diagramme de dispersion

Cet article explique ce que sont les diagrammes de dispersion. Vous découvrirez donc à quoi sert un nuage de points, comment réaliser un nuage de points, comment l’interpréter et des exemples de nuages de points.

Qu’est-ce qu’un nuage de points ?

Le nuage de points , ou nuage de points , est un type de diagramme statistique dans lequel un ensemble de données de deux variables est représenté graphiquement sur deux axes de coordonnées cartésiennes.

Par conséquent, les diagrammes de dispersion sont utilisés pour analyser la relation entre deux variables statistiques.

Les nuages de points portent plusieurs noms différents, tels que diagramme de corrélation ou nuage de points .

Il est à noter que le diagramme de dispersion est considéré comme l’un des outils de base du contrôle qualité, au même titre que le diagramme de Pareto, le diagramme de cause à effet, l’organigramme, etc.

Comment faire un nuage de points

Pour créer un diagramme de dispersion, vous devez suivre les étapes suivantes :

1. Collectez des données statistiques à partir de l’échantillon que vous souhaitez analyser. Gardez à l’esprit que pour créer un diagramme de dispersion, il doit y avoir au moins deux variables quantitatives.
2. Représentez les deux axes du nuage de points.
3. Déterminez les deux variables statistiques qui seront représentées graphiquement.
4. Calibrez l’échelle de chaque axe du graphique. Pour ce faire, il est recommandé de trouver d’abord le minimum et le maximum de chaque variable et, en fonction de ces valeurs, de graduer chaque axe.
5. Représentez chaque paire de données sur le nuage de points avec un point.
6. Analyser et interpréter le diagramme de dispersion obtenu.

Exemple de nuage de points

Après avoir vu la définition d’un diagramme de dispersion et la théorie sur sa réalisation, cette section représente un diagramme de ce type à titre d’exemple.

• Dans le tableau de fréquence suivant, les notes en mathématiques et en statistiques d’un échantillon de 20 élèves ont été collectées sous forme de données. Tracez l’ensemble de données sur un nuage de points et analysez-le.

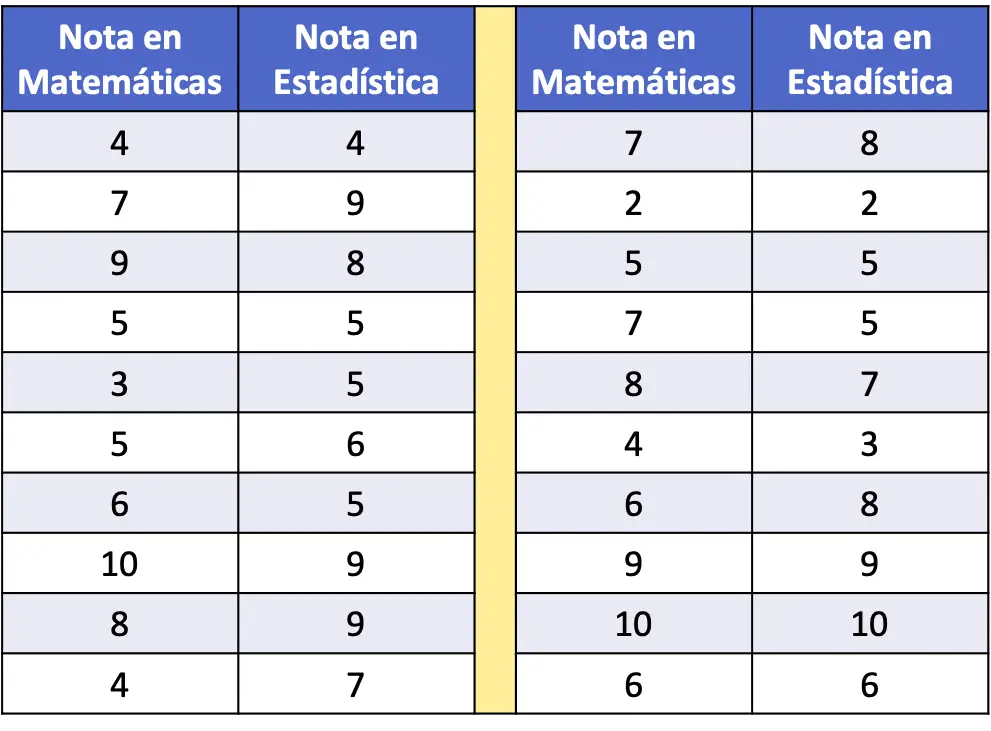
Pour représenter la série de données dans un diagramme de dispersion, nous devons simplement tracer deux axes, les calibrer et représenter un point sur le graphique pour chaque paire de données. N’oubliez pas qu’un point sur un graphique est placé à l’intersection des lignes imaginaires correspondant à chacune de ses valeurs.

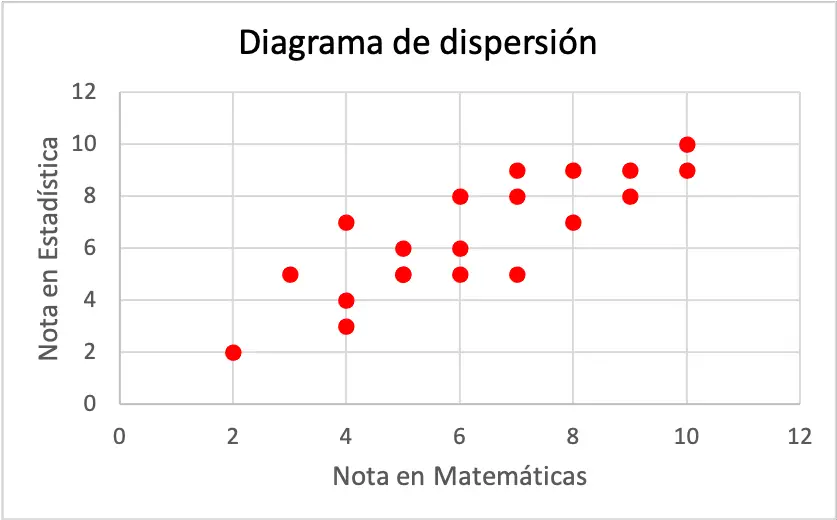
Chaque axe du nuage de points représente une variable. Plus précisément, l’axe horizontal appartient à la note obtenue en mathématiques et, d’autre part, l’axe vertical correspond à la note obtenue en statistiques.

Comme vous pouvez le voir sur le nuage de points, les deux variables ont une corrélation positive, car une variable augmente à mesure que l’autre variable augmente également. Par conséquent, on conclut que si un élève obtient une meilleure note en mathématiques, il est plus probable qu’il obtienne également une meilleure note en statistiques, et vice versa.

Cependant, la conclusion précédente ne signifie pas qu’une variable est la cause de l’autre, car obtenir une bonne note en mathématiques ne garantit pas automatiquement une bonne note en statistiques sans rien faire, mais il faut plutôt étudier les deux matières. Dans la section suivante, nous entrerons plus en détail sur ce concept.

Le diagramme de dispersion et la corrélation

À partir d’un diagramme de dispersion, il est possible d’identifier le type de corrélation entre deux variables :

• Corrélation directe (ou corrélation positive) : une variable augmente lorsque l’autre augmente également.
• Corrélation inverse (ou corrélation négative) : lorsqu’une variable augmente, l’autre diminue, et vice versa, si une variable diminue, l’autre augmente.
• Corrélation nulle (Pas de corrélation) : Il n’y a aucune relation entre les deux variables.

De même, que la corrélation entre les deux variables soit directe ou inverse, la corrélation peut également être classée en fonction de la force ou de la faiblesse de la relation entre les deux variables.

• Forte corrélation : les deux variables sont étroitement liées. Les points sont rapprochés sur le nuage de points. Il est donc plus facile d’identifier la relation entre les variables.
• Faible corrélation : Une relation existe entre les deux variables, mais elle est difficile à identifier. Les points sont éloignés les uns des autres sur le nuage de points.

D’un autre côté, la corrélation peut également être calculée numériquement à l’aide d’une formule, ce qui vous permet de savoir mathématiquement à quel point deux variables différentes sont étroitement liées. Pour voir comment cela se passe, cliquez sur le lien suivant :

Gardez à l’esprit que même s’il existe une corrélation entre deux variables, cela ne signifie pas qu’il existe une causalité entre elles, c’est-à-dire que la corrélation entre deux variables ne signifie pas que le changement d’une variable est la cause du changement de l’autre. variable.

Ainsi, à l’instar du nuage de points de la section précédente, bien qu’il existe une corrélation positive entre la note en mathématiques et la note en statistiques, obtenir une bonne note en mathématiques ne signifie pas obtenir une bonne note en statistiques, car si vous n’étudiez que les mathématiques, vous échouerez sûrement en statistiques. Par conséquent, les deux variables sont liées mais elles ne sont pas une cause et un effet.

Pour en savoir plus, vous pouvez continuer avec le post suivant :

Avantages et inconvénients du nuage de points

En raison des caractéristiques du nuage de points, ce type de graphique statistique présente des avantages et des inconvénients.

Avantage:

• Il est assez simple de représenter une série de données sur un nuage de points.
• Le nuage de points vous permet d’analyser visuellement la relation entre deux variables, ce qui facilite la conclusion.
• Les nuages de points peuvent également être utilisés dans une étude statistique approfondie comme exploration préliminaire des données.

Désavantages:

• Ces types de diagrammes ne sont pas utiles pour représenter des variables qualitatives.
• L’interprétation d’un diagramme de dispersion peut conduire à une conclusion erronée de cause à effet entre deux variables.
• Les nuages de points ne vous permettent pas d’analyser la relation entre plus de deux variables.