Mode (statistiques)

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est le mode dans les statistiques. Vous découvrirez comment trouver le mode statistique pour les données groupées et les données non groupées, les différents types de mode, et plusieurs exemples de cette mesure statistique.

Qu’est-ce que le mode en statistiques ?

En statistiques, le mode est la valeur de l’ensemble de données qui a la fréquence absolue la plus élevée, c’est-à-dire que le mode est la valeur la plus répétée dans un ensemble de données.

Par conséquent, pour calculer le mode d’un ensemble de données statistiques, il suffit de compter le nombre de fois où chaque élément de données apparaît dans l’échantillon, et les données les plus répétées seront le mode.

Le mode est utilisé pour définir une distribution statistique, puisque la valeur la plus répétée est généralement au centre de la distribution.

Le mode peut également être dit mode statistique ou valeur modale . De même, lorsque les données sont regroupées en intervalles, l’intervalle le plus répété est l’ intervalle modal ou la classe modale .

En général, le terme Mo est utilisé comme symbole du mode statistique, par exemple, le mode de distribution X est Mo(X).

Gardez à l’esprit que le mode est une mesure statistique de la position centrale, ainsi que de la médiane et de la moyenne. Ci-dessous, nous verrons ce que signifie chacune de ces mesures statistiques.

Types de mode dans les statistiques

En statistiques, il existe plusieurs types de modes qui sont classés selon le nombre de valeurs les plus répétées :

Mode unimodal : il n’y a qu’une seule valeur avec le nombre maximum de répétitions. Par exemple, [1, 4, 2, 4, 5, 3].
Mode bimodal : Le nombre maximum de répétitions se produit à deux valeurs différentes, et les deux valeurs sont répétées le même nombre de fois. Par exemple, [2, 6, 7, 2, 3, 6, 9].
Mode multimodal : Trois valeurs ou plus ont le même nombre maximum de répétitions. Par exemple, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

Comment trouver le mode statistique

Pour trouver le mode statistique d’un ensemble de données, vous devez suivre les étapes suivantes :

Mettez les données en ordre. Cette étape n’est pas obligatoire, mais elle vous permettra de compter plus facilement les nombres.
Comptez combien de fois chaque numéro apparaît.
Le nombre qui apparaît le plus souvent est le mode statistique.

Exemples de mode statistique

Compte tenu de la définition de la mode dans les statistiques, vous pouvez voir ci-dessous un exemple de chaque type de mode afin que vous puissiez mieux comprendre le concept.

Exemple de mode unimodale

Quel est le mode de l’ensemble de données suivant ?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

Les numéros ne sont pas ordonnés, nous allons donc les classer d’abord pour faciliter la recherche du mode.

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

Les chiffres 2 et 9 apparaissent deux fois, mais le chiffre 5 est répété trois fois. Par conséquent, le mode de la série de données est le numéro 5.

$Mo=5$

Exemple de mode bimodale

Calculez le mode de l’ensemble de données suivant :

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

Nous mettons d’abord les chiffres dans l’ordre :

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

Comme vous pouvez le constater, le chiffre 6 et le chiffre 8 apparaissent quatre fois au total, soit le nombre maximum de répétitions. Par conséquent, dans ce cas, il s’agit d’un mode bimodal et les deux nombres sont le mode de l’ensemble de données :

$Mo=\{ 6 \ ; \ 8\}$

Exemple de mode multimodale

Recherchez le mode de l’ensemble de données suivant :

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

Comme il y a beaucoup de données, nous les trions d’abord par ordre croissant pour faciliter leur comptage :

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

Les nombres les plus répétés sont 20, 27 et 31, les trois nombres sont répétés cinq fois. Le mode de cet exemple est donc multimodal.

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

calculateur de mode

Entrez les données de n’importe quel échantillon statistique dans la calculatrice en ligne suivante pour calculer son mode. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Mode pour les données groupées

Lorsqu’on a les données regroupées sous forme d’intervalles, on ne sait pas vraiment combien de fois chaque donnée est répétée, on connaît seulement la fréquence de chaque intervalle.

Ainsi, pour calculer le mode des données regroupées en intervalles, il faut utiliser la formule suivante :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

Où:

L _i est la limite inférieure de l’intervalle modal (intervalle de fréquence absolue la plus élevée).
f _i est la fréquence absolue de l’intervalle modal.
f _i-1 est la fréquence absolue de l’intervalle avant le modal.
f _i+1 est la fréquence absolue de l’intervalle après le modal.
A _i est la largeur de l’intervalle modal.

À titre d’exemple, vous avez résolu ci-dessous un exercice dans lequel le mode des données regroupées en intervalles est calculé :

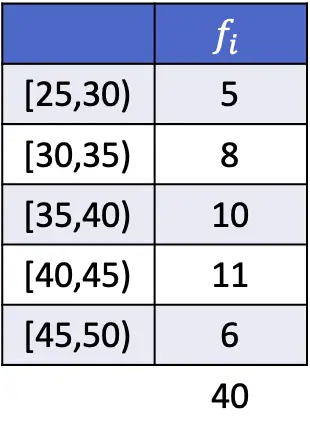
exemple de mode statistique pour données groupées

Dans ce cas, l’intervalle modal est [40,45), puisque c’est l’intervalle avec la plus grande fréquence absolue. Par conséquent, les paramètres de la formule de mode pour les données groupées sont :

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

On applique donc la formule pour déterminer le mode des données regroupées en intervalles et on fait le calcul :

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

Différence entre mode, moyenne et médiane

Dans cette dernière section nous verrons quelle est la différence entre le mode, la moyenne et la médiane. Puisque tous les trois sont des mesures statistiques de position centrale, leur signification est différente.

Comme expliqué tout au long de l’article, le mode en mathématiques est la valeur la plus répétée dans un ensemble de données.

Deuxièmement, la moyenne est la valeur moyenne de toutes les données statistiques. Ainsi, pour obtenir la moyenne de certaines données, il faut additionner toutes les données puis diviser le résultat par le nombre d’observations.

Et enfin, la médiane est la valeur qui occupe la position centrale lorsque les données sont ordonnées.

Ainsi, les trois mesures statistiques aident à définir une distribution de probabilité, car elles permettent de se faire une idée de ses valeurs centrales. Mais gardez à l’esprit qu’il n’existe pas de mesure meilleure qu’une autre, elles désignent simplement des concepts différents.

Propriétés de la mode

Les propriétés de la mode sont les suivantes :

Le mode peut être trouvé à la fois dans les variables quantitatives et les variables qualitatives.
Si l’on applique une transformation linéaire à une variable aléatoire, la valeur de la moyenne changera en fonction des opérations appliquées.
$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$
En général, le mode est insensible aux valeurs aberrantes.
Si toutes les valeurs ont la même fréquence, il n’y a pas de mode.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus