Médian

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la médiane d’un ensemble de données et comment trouver la médiane pour les données non groupées et les données groupées. De plus, vous pouvez calculer la médiane de n’importe quelle série de données avec le calculateur en ligne à la fin.

Quelle est la médiane ?

En statistiques, la médiane est la valeur médiane de toutes les données classées de la plus petite à la plus grande. Autrement dit, la médiane divise l’ensemble des données ordonnées en deux parties égales.

La médiane est une mesure de la position centrale utilisée pour décrire une distribution de probabilité.

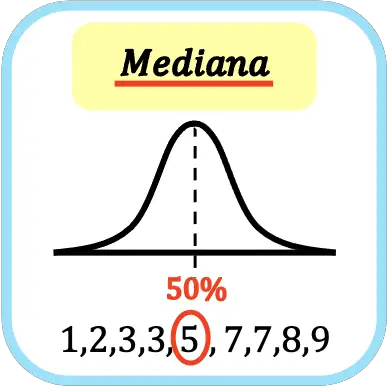
👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la médiane de n’importe quel ensemble de données.

En général, le terme Moi est souvent utilisé comme symbole du médian.

Les autres mesures de position centrale sont la moyenne et le mode, nous verrons ci-dessous les différences entre elles. De même, les mesures de position non centrale sont les quartiles, les quintiles, les déciles, les centiles, etc.

Il convient de noter que la médiane d’un ensemble de données coïncide avec le deuxième quartile, le cinquième décile et le 50e percentile.

Comment calculer la médiane

Le calcul de la médiane dépend du fait que le nombre total de données soit pair ou impair :

Si le nombre total de données est impair , la médiane sera la valeur qui se situe en plein milieu des données. C’est-à-dire la valeur qui se trouve en position (n+1)/2 des données triées.

$Me=x_{\frac{n+1}{2}$

Si le nombre total de données est pair , la médiane sera la moyenne des deux données situées au centre. C’est-à-dire la moyenne arithmétique des valeurs qui se trouvent aux positions n/2 et n/2+1 des données ordonnées.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Où

$n$ est le nombre total de données dans l’échantillon.

Exemples de calcul de la médiane

Afin que vous puissiez voir comment la médiane est calculée, vous trouverez ci-dessous deux exemples concrets, un pour chaque cas. Tout d’abord, la médiane d’un ensemble de données impair sera calculée, puis la médiane sera calculée avec un ensemble de données pair.

Médiane des données impaires

Calculez la médiane des données suivantes : 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5

La première chose que nous devons faire avant d’effectuer des calculs est d’ordonner les données, c’est à dire que nous mettons les nombres du plus petit au plus grand.

$1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8$

Dans ce cas, nous avons 11 observations, le nombre total de données est donc impair. Par conséquent, nous appliquons la formule suivante pour calculer la position de la médiane :

$\cfrac{n+1}{2}=\cfrac{11+1}{2}=6$

La médiane sera donc la donnée qui se trouve en sixième position, ce qui correspond dans ce cas à la valeur 4.

$Me=x_6=4$

médiane des données paires

Quelle est la médiane des observations suivantes ? 2, 6, 2, 8, 9, 4, 7, 11, 4, 13

Pour obtenir la médiane, il faut d’abord classer toutes les données par ordre croissant :

$2 \ 2 \ 4 \ 4 \ 6 \ 7 \ 8 \ 9 \ 11 \ 13$

Cet exemple est différent du précédent, puisque cette fois nous avons un total de 10 observations, ce qui est un nombre pair. Par conséquent, la procédure de détermination de la moyenne est un peu plus compliquée.

Il faut d’abord calculer les deux positions centrales entre lesquelles se trouvera la médiane, pour cela il faut appliquer les deux formules suivantes :

$\cfrac{n}{2}=\cfrac{10}{2}=5$

$\cfrac{n}{2}+1=\cfrac{10}{2}+1=6$

La médiane se situera donc entre la cinquième et la sixième position, qui correspondent respectivement aux valeurs 6 et 7. Concrètement, la médiane sera la moyenne arithmétique desdites valeurs :

$Me=\cfrac{x_5+x_6}{2}=\cfrac{6+7}{2}=6,5$

calculateur médian

Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer sa médiane. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Médiane pour les données groupées

Pour calculer la médiane lorsque les données sont regroupées en intervalles, il faut d’abord trouver l’intervalle ou la classe dans laquelle se situe la médiane à l’aide de la formule suivante :

$\cfrac{n+1}{2}$

Ainsi, la médiane sera dans l’intervalle dont la fréquence absolue cumulée est immédiatement supérieure au nombre obtenu avec l’expression algébrique précédente.

Et une fois que l’on connaît l’intervalle auquel appartient la médiane, il faut appliquer la formule suivante pour trouver la valeur exacte de la médiane :

$Me=L_i+ \cfrac{\displaystyle\frac{n+1}{2}-F_{i-1}}{f_i}\cdot I_i$

Où:

L _i est la limite inférieure de l’intervalle dans lequel se trouve la médiane.
n est le nombre total d’observations.
F _i-1 est la fréquence absolue accumulée de l’intervalle précédent.
f _i est la fréquence absolue de l’intervalle dans lequel se situe la médiane.
I _i est la largeur de l’intervalle médian.

À titre d’exemple, vous avez résolu ci-dessous un exercice dans lequel la médiane de données regroupées en intervalles est calculée.

Pour trouver la médiane de l’ensemble de données, nous devons d’abord déterminer l’intervalle dans lequel elle se situe. Pour ce faire, nous utilisons la formule suivante :

$\cfrac{n+1}{2}=\cfrac{30+1}{2} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

Donc la médiane sera dans l’intervalle dont la fréquence absolue cumulée est immédiatement supérieure à 15,5, qui dans ce cas est l’intervalle [60,70) dont la fréquence absolue cumulée est 26. Et une fois qu’on connaît l’intervalle médian, on applique la deuxième formule du processus :

$Me=L_i+ \cfrac{\displaystyle\frac{n+1}{2}-F_{i-1}}{f_i}\cdot I_i$

$Me=60+\cfrac{\displaystyle\frac{30+1}{2}-15}{11}\cdot 10=60,45$

En fin de compte, la médiane de l’ensemble de données regroupées est de 60,45. Comme vous pouvez le constater, dans ce type de problèmes, la médiane est généralement un nombre décimal.

médiane, moyenne et mode

Dans cette dernière section nous verrons quelle est la différence entre la médiane, la moyenne et le mode. Eh bien, ce sont trois mesures statistiques de position centrale mais leur signification est différente.

Comme nous l’avons vu, la médiane est définie comme la valeur qui occupe la position centrale lorsque les données sont ordonnées.

En revanche, la moyenne est la valeur moyenne de toutes les données statistiques. Pour calculer la moyenne, vous devez additionner toutes les données puis diviser le résultat par le nombre de données.

Enfin, le mode est la valeur la plus répétée d’une série de données.

Comme vous pouvez le constater, les trois mesures statistiques aident à décrire une distribution de probabilité, puisqu’elles permettent de se faire une idée de ses valeurs centrales. Cependant, aucune mesure n’est meilleure qu’une autre, elles désignent simplement des concepts différents.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus