Coefficient de corrélation de Pearson
Cet article explique ce qu’est le coefficient de corrélation de Pearson (ou coefficient de corrélation linéaire) et à quoi il sert. Vous découvrirez comment calculer le coefficient de corrélation de Pearson ainsi qu’un exercice étape par étape. De plus, vous pouvez trouver la valeur du coefficient de corrélation de Pearson de n’importe quel ensemble de données avec le calculateur en ligne à la fin.
Qu’est-ce que le coefficient de corrélation de Pearson ?
Le coefficient de corrélation de Pearson , également appelé coefficient de corrélation linéaire ou simplement coefficient de corrélation , est une mesure statistique qui indique la relation entre deux variables.
Pour calculer le coefficient de corrélation de Pearson entre deux variables, il faut diviser la covariance desdites variables par la racine carrée du produit de leurs variances.
Ainsi, le coefficient de corrélation de Pearson tente de quantifier la dépendance linéaire entre deux variables aléatoires quantitatives. A priori, valorar numéricamente la correlación entre dos variables es complicado porque resulta difícil determinar qué pareja de variables está más correlacionada entre sí, así pues, el objetivo de coeficiente de correlación de Pearson es dar un valor a la relación entre variables para luego poder comparar entre elles.
La valeur de l’indice de corrélation de Pearson est comprise entre -1 et +1 inclus. Nous verrons ci-dessous comment est interprétée la valeur du coefficient de corrélation de Pearson.
Formule du coefficient de corrélation de Pearson
Le coefficient de corrélation de Pearson de deux variables statistiques est égal au quotient entre la covariance des variables et la racine carrée du produit de la variance de chaque variable.
Par conséquent, la formule de calcul du coefficient de corrélation de Pearson est la suivante :
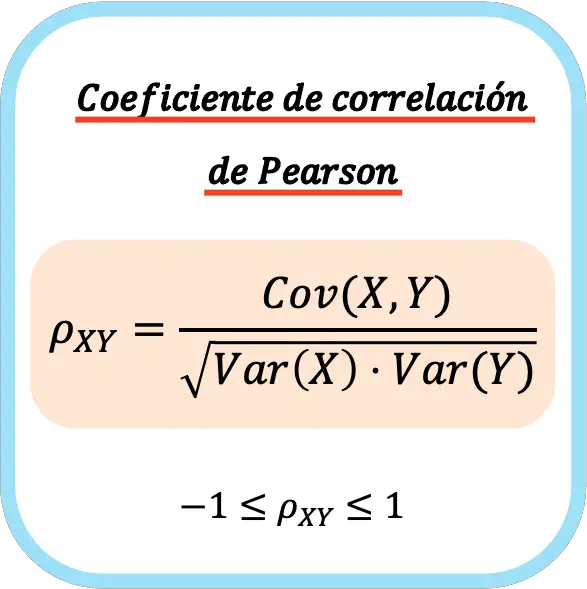
👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer le coefficient de corrélation de Pearson pour n’importe quel ensemble de données.
Lorsque le coefficient de corrélation de Pearson est calculé sur une population, il est généralement exprimé par la lettre grecque ρ. Mais lorsque le coefficient est calculé par rapport à un échantillon, la lettre r est généralement utilisée comme symbole.
Gardez à l’esprit que pour déterminer le coefficient de corrélation de Pearson, il est essentiel que vous sachiez comment calculer la covariance entre deux variables et la variance d’une variable. De plus, vous devez comprendre ce que signifient ces mesures statistiques. Par conséquent, avant de poursuivre l’explication, il est recommandé de lire les deux articles suivants :
Exemple de calcul du coefficient de corrélation de Pearson
Compte tenu de la définition du coefficient de corrélation de Pearson et de sa formule, vous trouverez ci-dessous un exemple étape par étape afin que vous puissiez voir comment il est calculé.
- Calculez le coefficient de corrélation de Pearson entre les deux variables continues suivantes :

Avant de calculer le coefficient de corrélation de Pearson, nous représenterons l’ensemble de données dans un nuage de points pour analyser la relation entre les deux variables :
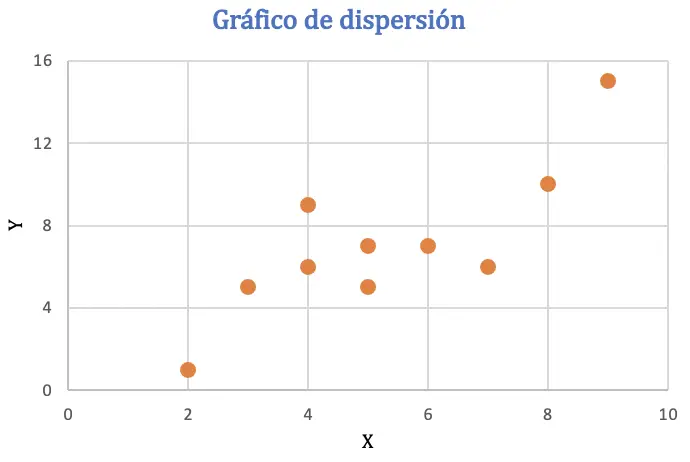
À partir du diagramme de dispersion, on peut déduire que les données peuvent avoir une tendance positive, ou en d’autres termes, lorsqu’une variable augmente en valeur, l’autre variable augmente également. Pour vérifier la corrélation, nous allons trouver le coefficient de Pearson.
La première chose à faire est de trouver la moyenne arithmétique de chaque variable séparément, ce qui équivaut à la somme totale des données divisée par le nombre d’observations.
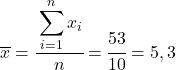
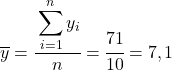
Maintenant que nous connaissons la moyenne de chaque variable, nous devons ajouter les colonnes suivantes au tableau de données :
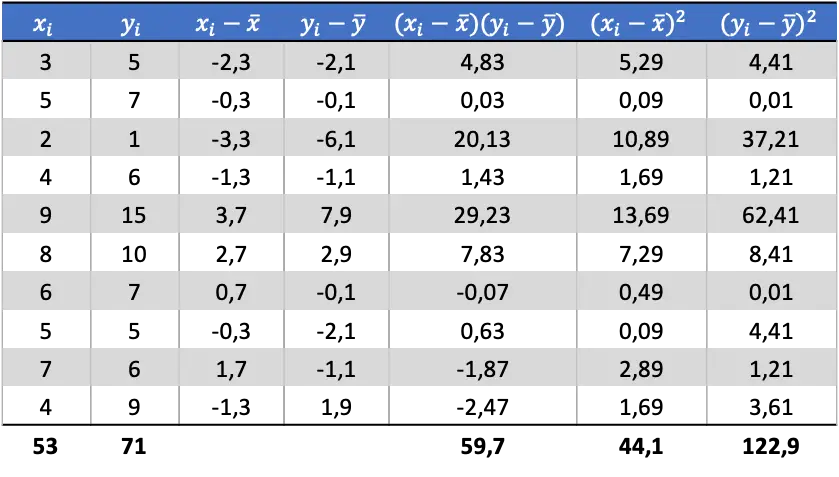
A partir des données calculées dans le tableau, nous déterminons les valeurs de la covariance et des variances (si vous ne vous souvenez pas comment cela a été fait, il y a deux liens ci-dessus où cela est expliqué en détail) :
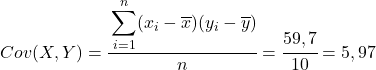
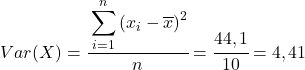
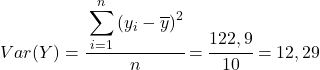
Finalement, il suffit d’appliquer la formule du coefficient de corrélation de Pearson pour obtenir sa valeur :
![]()
Le coefficient de corrélation de Pearson a une valeur très proche de 1, ce qui signifie que ces deux variables ont une corrélation positive assez forte.
Comme vous l’avez vu, pour déterminer le coefficient de corrélation de Pearson, il est très utile d’utiliser des programmes tels qu’Excel pour effectuer plus rapidement les calculs de colonnes.
Calculateur du coefficient de corrélation de Pearson
Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer le coefficient de corrélation de Pearson entre deux variables. Vous devez séparer les paires de données, de sorte que dans la première case il n’y ait que les valeurs d’une variable et dans la deuxième case il n’y ait que les valeurs de la deuxième variable.
Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.
Interpréter le coefficient de corrélation de Pearson
Dans cette section, nous verrons comment interpréter le coefficient de corrélation de Pearson, car il ne suffit pas de connaître sa valeur, mais il faut savoir analyser sa signification.
Ainsi l’ interprétation du coefficient de corrélation de Pearson dépend de sa valeur :
- r=-1 : les deux variables ont une corrélation négative parfaite, on peut donc tracer une ligne avec une pente négative dans laquelle se trouvent tous les points.
- -1<r<0 : la corrélation entre les deux variables est négative, donc lorsqu’une variable augmente l’autre diminue. Plus la valeur est proche de -1, plus les variables sont liées négativement.
- r=0 : la corrélation entre les deux variables est très faible, en effet, la relation linéaire entre elles est nulle. Cela ne signifie pas que les variables sont indépendantes, puisqu’elles pourraient avoir une relation non linéaire.
- 0<r<1 : la corrélation entre les deux variables est positive, plus la valeur est proche de +1, plus la relation entre les variables est forte. Dans ce cas, une variable a tendance à augmenter en valeur lorsque l’autre augmente également.
- r=1 : les deux variables ont une corrélation positive parfaite, c’est-à-dire qu’elles ont une relation linéaire positive.
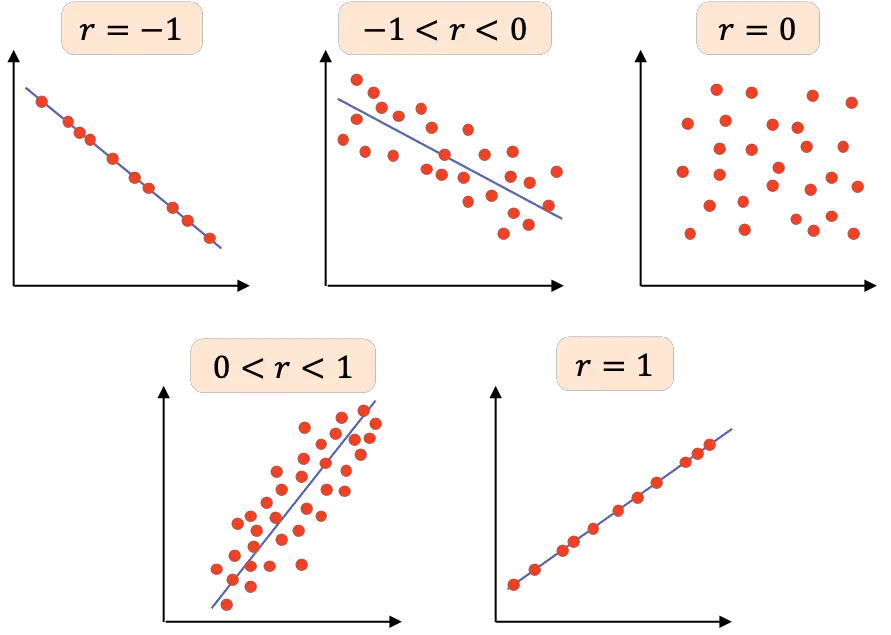
En synthèse, le tableau suivant est présenté avec les différentes interprétations du coefficient de corrélation de Pearson :
| Valeur | Interprétation |
|---|---|
| r=-1 | Corrélation négative parfaite. |
| -1<r<0 | Corrélation négative : plus la corrélation est proche de -1, plus elle est forte. |
| r=0 | Corrélation linéaire nulle. |
| 0<r<1 | Corrélation positive : plus la corrélation est proche de +1, plus elle est forte. |
| r=1 | Corrélation positive parfaite. |
Gardez à l’esprit que même s’il existe une relation entre deux variables, cela ne signifie pas qu’il existe une causalité entre elles, c’est-à-dire que la corrélation entre deux variables ne signifie pas que le changement d’une variable est la cause du changement de la variable. autre variable.
Par exemple, si nous constatons qu’il existe une relation positive entre la production de deux hormones différentes dans le corps, il n’est pas nécessaire qu’une augmentation d’une hormone entraîne une augmentation de l’autre hormone. Il se pourrait que le corps produise les deux hormones parce qu’il a besoin des deux pour combattre une maladie et qu’il augmente donc le niveau des deux simultanément, dans ce cas la cause serait la maladie. Pour déterminer s’il existe un lien de causalité entre les deux hormones, une étude plus approfondie devrait être réalisée.
