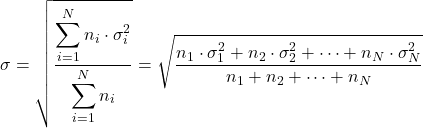Écart type (ou écart type)

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est l’écart type, également appelé écart type. Vous découvrirez comment calculer l’écart type, un exemple pratique étape par étape et un calculateur en ligne pour trouver l’écart type de n’importe quel échantillon de données.

Quel est l’écart type (ou écart type) ?

L’ écart type , également appelé écart type , est une mesure de dispersion statistique. Autrement dit, l’écart type est une valeur qui indique la dispersion d’un ensemble de données statistiques.

Par conséquent, l’écart type (ou écart type) sert à quantifier la dispersion d’une population ou d’un échantillon statistique. Plus l’écart type d’une série de données est grand, plus les données sont dispersées. Et l’interprétation peut aussi se faire dans l’autre sens, si l’écart type est faible cela signifie qu’en général la donnée est très proche de sa moyenne.

Lors du calcul de l’écart type ou typique sur une population, le symbole de l’écart type est la lettre grecque sigma (σ). Mais lorsqu’il s’agit d’un écart type d’échantillon, la lettre s est utilisée pour représenter la mesure statistique.

Dans certains livres de statistiques et de probabilités, l’écart type est également appelé écart type.

Formule d’écart type (ou écart type)

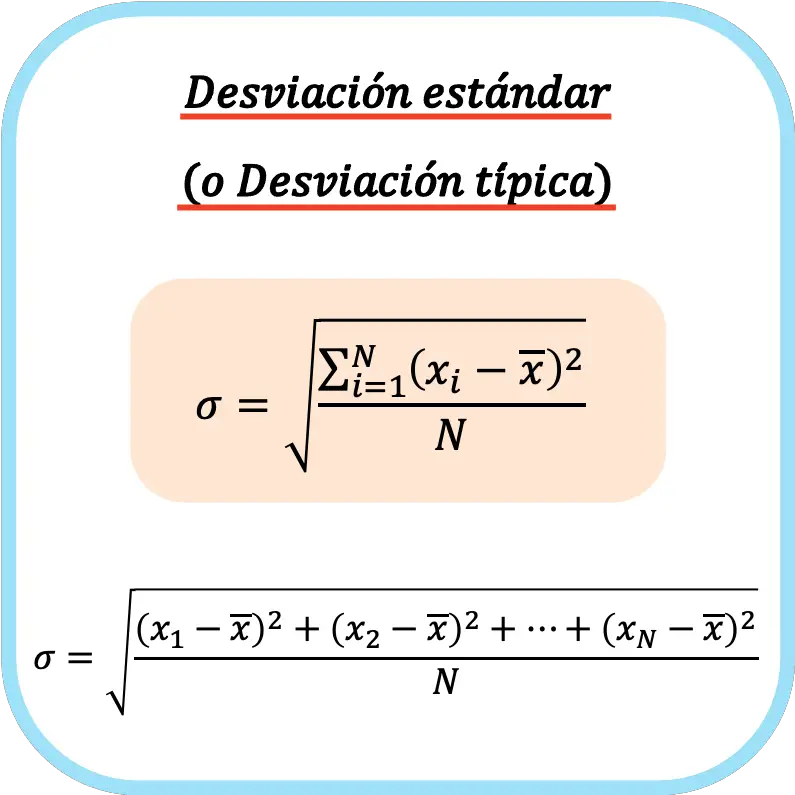
L’écart type (ou écart type) est égal à la racine carrée de la somme des carrés des écarts de la série de données divisée par le nombre total d’observations.

La formule pour calculer l’écart type (ou écart type) est donc :

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer l’écart type de n’importe quel ensemble de données.

En conclusion, pour trouver l’écart type d’un ensemble de données, vous devez calculer tous les écarts (définis comme la différence entre un point de données et la moyenne arithmétique), augmenter les écarts à deux, les additionner tous, puis diviser par le total. nombre de données, et enfin prendre la racine carrée.

Exemple d’écart type (ou écart type)

Compte tenu de la définition de l’écart type (ou écart typique), vous trouverez ci-dessous un exemple étape par étape afin que vous puissiez voir comment l’écart type d’une série de données est calculé.

Calculez l’écart type des valeurs suivantes : 3, 6, 2, 9, 4.

La première chose que nous devons faire est de déterminer la moyenne de l’échantillon. Pour ce faire, nous additionnons toutes les données et divisons par le nombre total d’observations, qui est de cinq :

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Nous utilisons maintenant la formule de l’écart type :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Nous substituons les données dans la formule :

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

Et enfin on calcule l’écart type :

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Calculateur d’écart type (ou d’écart type)

Entrez un ensemble de données statistiques dans le calculateur en ligne suivant pour calculer son écart type (ou écart type). Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Écart type (ou typique) pour les données groupées

Pour calculer l’écart type (ou écart type) des données regroupées en intervalles , les étapes suivantes doivent être suivies :

Trouvez la moyenne des données groupées.
Calculez les écarts des données groupées.
Mettez au carré chaque écart.
Multipliez chaque résultat précédent par la fréquence de son intervalle.
Additionnez la somme de toutes les valeurs obtenues à l’étape précédente.
Divisez par le nombre total d’observations.
Prenez la racine carrée de la valeur précédente. Le nombre obtenu est l’écart type des données groupées.

En conclusion, la formule pour calculer l’écart type des données regroupées en intervalles est :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

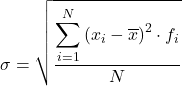
Bien que la formule ci-dessus soit normalement utilisée, l’expression algébrique suivante peut également être utilisée puisque le même résultat est obtenu :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

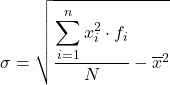
Pour que vous puissiez voir comment cela se fait, vous trouverez ci-dessous un exercice étape par étape sur l’écart type des données regroupées en intervalles. Plus précisément, l’écart type des données statistiques suivantes sera calculé :

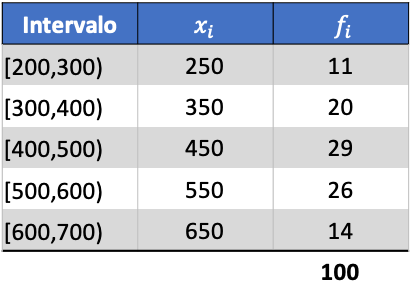
exemple de données regroupées en intervalles

Tout d’abord, on multiplie la note de classe de chaque intervalle par sa fréquence afin de calculer la moyenne arithmétique :

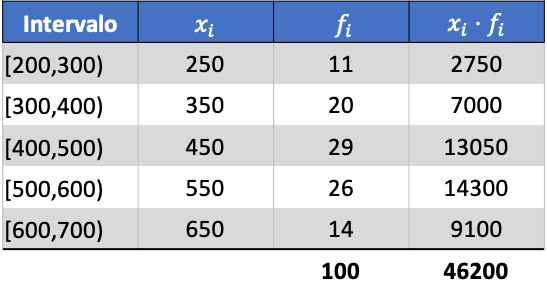
Ainsi la moyenne des données regroupées sera :

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

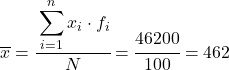
Maintenant que nous connaissons la valeur de la moyenne, nous devons ajouter les trois colonnes suivantes au tableau de données :

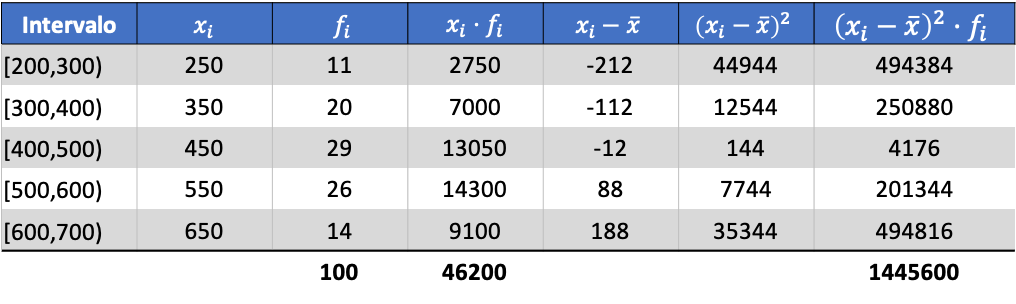
exercice résolu de l'écart type ou écart type pour données groupées

Ensuite, l’écart type des données regroupées sera le résultat de la racine carrée du total de la dernière colonne divisée par le nombre total d’observations :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

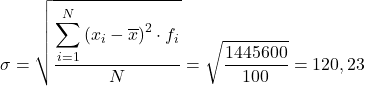
Écart type (ou typique) et variance

La relation entre l’écart type (ou écart typique) et la variance est que l’écart type est la racine carrée de la variance.

Ainsi, si nous connaissons la valeur de variance d’un ensemble de données, nous pouvons facilement calculer l’écart type en prenant la racine carrée. Ou inversement, si nous connaissons l’écart type, nous pouvons trouver la variance en mettant la valeur au carré.

$Var(X)=\sigma^2$

En fait, la variance peut être représentée simplement en utilisant le symbole de l’écart type carré. Par conséquent, le symbole de la variance de la population est sigma au carré (σ ² ) et le symbole de la variance de l’échantillon est s au carré (s ² ).

De plus, les concepts d’écart type et de variance ont une interprétation similaire, puisque tous deux montrent la dispersion d’une série de données statistiques.

Propriétés de l’écart type (ou écart type)

L’écart type a les propriétés suivantes :

L’écart type d’un échantillon de données ne peut pas être négatif.

$\sigma \ge 0$

L’écart type sera égal à zéro si toutes les données sont identiques.

$\sigma =0$

Si un terme constant est ajouté à toutes les données, la valeur de l’écart type ne change pas.

$\sigma (X+k)=\sigma (X)$

Si toutes les données sont multipliées par un nombre, l’écart type sera multiplié par la valeur absolue dudit nombre.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

L’écart type de la somme de deux variables aléatoires est égal à la racine carrée de la somme des variances des variables plus deux fois la covariance entre les deux variables.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Si nous connaissons les écarts types des différentes distributions (σ _i ) et leur nombre de données (n _i ), nous pouvons calculer l’écart type total en appliquant la formule suivante :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus