Écart moyen

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est l’écart moyen et comment il est calculé. Vous trouverez également des exemples concrets de calcul de l’écart moyen. Et, en outre, vous pourrez calculer l’écart moyen de n’importe quel ensemble de données statistiques à l’aide d’un calculateur en ligne.

Qu’est-ce que l’écart moyen ?

L’ écart moyen , également appelé écart moyen absolu , est une mesure de dispersion statistique.

L’écart moyen d’un ensemble de données est la moyenne des écarts absolus . Par conséquent, l’écart moyen est égal à la somme des écarts de chaque donnée par rapport à la moyenne arithmétique divisée par le nombre total de données.

Autrement dit, la formule de l’écart moyen est la suivante :

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer l’écart moyen de n’importe quel ensemble de données.

En statistique, l’écart moyen est également appelé écart moyen absolu .

L’interprétation de l’écart moyen se fait de la manière suivante : plus la valeur de l’écart moyen est grande, cela signifie que les données sont, en moyenne, plus éloignées de la moyenne arithmétique ; à l’inverse, plus l’écart moyen est faible, plus la valeur est proche. les données sont. L’écart moyen indique donc la dispersion d’une série de données.

Les autres mesures considérées comme réparties sont l’intervalle, l’intervalle interquartile, l’écart type (ou écart type), la variance et le coefficient de variation.

Comment calculer l’écart moyen

Pour calculer l’écart moyen d’une série de données, les étapes suivantes doivent être suivies :

Calculez la moyenne arithmétique de l’ensemble de données statistiques.
Calculez l’écart de chaque donnée par rapport à la moyenne, défini comme la valeur absolue de la différence entre les données et la moyenne.
Additionnez tous les écarts calculés à l’étape précédente.
Divisez par le nombre total de données. Le résultat obtenu est l’écart moyen de la série de données.

En résumé, la formule qu’il faut appliquer pour trouver l’écart moyen est :

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Exemple de calcul de l’écart moyen

Compte tenu de la définition de l’écart moyen, vous trouverez ci-dessous un exemple résolu étape par étape de calcul de l’écart moyen d’un échantillon statistique. De cette façon, vous comprendrez mieux comment obtenir l’écart moyen.

Un analyste étudie les résultats économiques d’une entreprise au cours de l’année écoulée et dispose d’informations sur le bénéfice obtenu par l’entreprise au cours de chaque trimestre de ladite année : 2, 3, 7 et 5 millions de dollars. Quel est l’écart moyen des données ?

Tout d’abord, nous devons calculer la moyenne des données, nous faisons donc la somme et divisons par le nombre total d’observations (4) :

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

Une fois que nous avons calculé la moyenne arithmétique, nous utilisons la formule d’écart moyen :

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Nous substituons les données dans la formule :

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

On fait les calculs au numérateur :

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

Et enfin, on divise par le nombre total de données pour obtenir l’écart moyen de l’échantillon :

$D_{\overline{x}}=1,75$

Calculateur d’écart moyen

Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer son écart moyen. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Écart moyen pour les données groupées

Pour calculer l’écart moyen des données regroupées en intervalles, les étapes suivantes doivent être suivies :

Déterminez la moyenne arithmétique de l’ensemble de données statistiques. Puisque les données sont regroupées, l’expression pour calculer la moyenne est :

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

Calculez l’écart de chaque intervalle par rapport à la moyenne, qui équivaut à la valeur absolue de la différence entre la note de classe et la moyenne.

$|x_i-\overline{x}|$

Multipliez l’écart de chaque intervalle par sa fréquence absolue.

$|x_i-\overline{x}|\cdot f_i$

Additionnez tous les résultats de l’étape précédente, puis divisez par le nombre total de données. Le résultat obtenu est l’écart moyen de l’échantillon regroupé en intervalles.

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

En conclusion, la formule pour obtenir l’écart moyen à partir de données groupées est la suivante :

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Lorsque les données sont regroupées, cela signifie généralement qu’il y a beaucoup de données et que trouver l’écart moyen implique de nombreuses étapes. Par conséquent, des tableaux de fréquences sont généralement utilisés pour effectuer le calcul.

Vous trouverez ci-dessous un exercice étape par étape sur la façon de calculer l’écart moyen lorsque les données sont regroupées en intervalles :

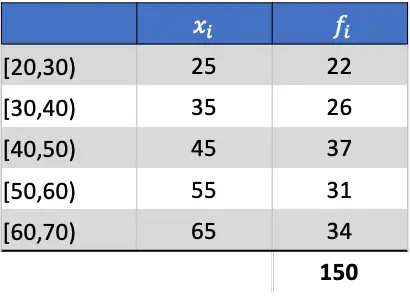
La première chose à faire est de calculer la moyenne des données regroupées. Pour ce faire, on ajoute une colonne au tableau en multipliant la note de classe par sa fréquence :

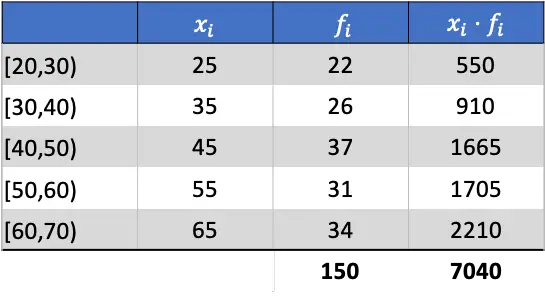
La moyenne arithmétique sera donc le résultat de la division de la somme de la colonne ajoutée par la somme des fréquences absolues :

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

Maintenant que nous connaissons la moyenne des données, nous pouvons ajouter toutes les colonnes nécessaires pour trouver l’écart moyen :

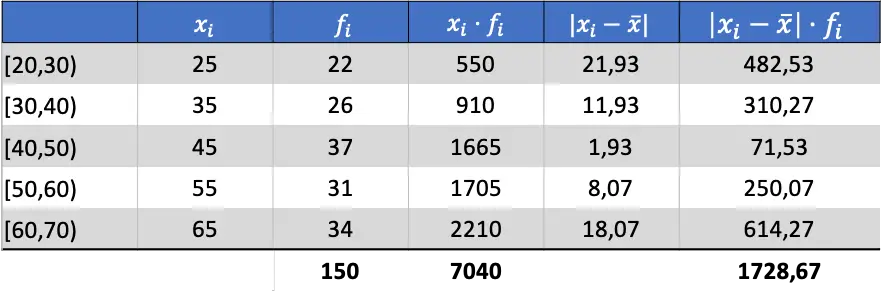
Ainsi, pour obtenir l’écart moyen il faut diviser la somme de la dernière colonne par le nombre total d’observations :

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus