Types de moyenne (statistiques)

Par Pr Amélia Rodriguez août 6, 2023 Statistiques 0 commentaire

Nous expliquons ici ce que sont tous les types de moyennes en statistiques et comment elles sont calculées. Vous trouverez la formule pour chaque type de bas et des exemples.

Mais avant de voir quels sont les types de moyenne, il faut logiquement savoir ce qu’est une moyenne en statistique. C’est pourquoi nous vous recommandons de consulter le lien suivant avant de continuer.

➤ Voir : Quelle est la moyenne (statistiques) ?

Quels sont les types de moyenne en statistiques ?

En statistiques, les types de moyennes sont :

Moyenne arithmétique
Moyenne pondérée
Moyenne géométrique
moyenne quadratique
moyenne harmonique
moyenne généralisée
moyenne f-généralisée
moyenne tronquée
moyenne interquartile
moyenne d’une fonction

Nous allons ensuite expliquer comment calculer tous les types de moyennes en statistiques. Les cinq types de moyenne les plus utilisés sont la moyenne arithmétique, la moyenne pondérée, la moyenne géométrique, la moyenne quadratique et la moyenne harmonique. Nous allons donc entrer plus en détail sur ces cinq principaux types de médias.

Moyenne arithmétique

La moyenne arithmétique est calculée en additionnant toutes les valeurs puis en divisant par le nombre total de données.

La formule de la moyenne arithmétique est donc la suivante :

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

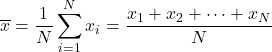
La moyenne arithmétique est également connue sous le nom de moyenne arithmétique .

La moyenne arithmétique est probablement le type de moyenne le plus utilisé en statistique.

Pour voir un exemple de la façon dont ce type de moyenne est obtenu, nous allons calculer la moyenne arithmétique des données suivantes :

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Pour calculer la moyenne arithmétique, il suffit d’additionner toutes les données statistiques et de diviser par le nombre total de données, qui est 6 :

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Moyenne pondérée

Pour calculer la moyenne pondérée, il faut d’abord multiplier chaque donnée statistique par son poids (ou poids), puis additionner tous les produits, et enfin diviser la somme pondérée par la somme de tous les poids.

La formule de moyenne pondérée est donc la suivante :

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

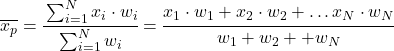
Où x _i est la valeur statistique et w _i son poids correspondant.

La moyenne pondérée est plus difficile à comprendre, nous vous recommandons donc de consulter l’exemple suivant qui explique étape par étape comment elle est calculée :

➤ Voir : Exemple de moyenne pondérée

Moyenne géométrique

La moyenne géométrique d’un ensemble de données statistiques est égale à la nième racine du produit de toutes les valeurs.

Ce type de moyenne est utilisé en finance d’entreprise pour calculer les taux de rendement, les moyennes en pourcentage et les intérêts composés.

La formule pour ce type de bas est assez compliquée. En fait, la moyenne géométrique de tous les ensembles statistiques ne peut pas être calculée, mais il arrive parfois que ce type de moyenne ne puisse pas être déterminé. C’est pourquoi nous vous recommandons de consulter toutes les exceptions expliquées dans le lien suivant :

➤ Voir : formule de moyenne géométrique

moyenne quadratique

La moyenne quadratique est égale à la racine carrée de la moyenne arithmétique des carrés des données.

La formule du carré moyen est donc la suivante :

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Ce type de moyenne est également appelé racine carrée moyenne , racine carrée moyenne ou RMS .

Précisons simplement que la moyenne cubique existe aussi, mais elle est utilisée dans des cas très particuliers.

La moyenne carrée présente des avantages et des inconvénients, par exemple, elle est particulièrement utile lorsque la variable statistique prend des valeurs positives et négatives, car en mettant au carré chaque donnée, toutes les valeurs deviennent positives. Vous pouvez voir plus de fonctionnalités de ce type de média en cliquant sur le lien suivant :

➤ Voir : avantages et inconvénients de la moyenne quadratique

moyenne harmonique

La moyenne harmonique est calculée en divisant le nombre total de données statistiques par la somme des inverses de chaque valeur.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

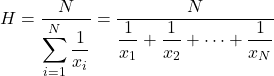
La moyenne harmonique est utilisée pour calculer des moyennes de vitesses, de temps ou faire des calculs électroniques. Cette caractéristique différencie la moyenne harmonique des autres types de moyennes, fréquemment utilisées dans le calcul de moyennes de prix ou de pourcentages.

Vous pouvez voir des exemples de calcul de ce type de moyenne sur la page suivante :

➤ Voir : exemples de moyenne harmonique

Autres types de bas

Dans cette section, nous verrons les formules pour d’autres types de bas. Nous n’entrerons pas dans les détails de chaque type car ils ne sont pas très utilisés, mais il est bon que vous sachiez qu’il existe d’autres types de bas.

La moyenne généralisée est un mélange des types de moyenne vus ci-dessus et est calculée à l’aide de la formule suivante :

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

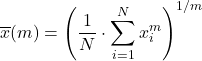
Soit f une fonction injective et monotone, alors la f-moyenne généralisée définie comme :

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

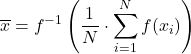
La moyenne tronquée consiste à calculer la moyenne arithmétique après avoir soustrait un pourcentage d’observations aux extrémités supérieure et inférieure de l’échantillon. Le même pourcentage doit être rejeté aux deux extrémités.

Pour calculer la moyenne interquartile , également appelée moyenne interquartile, les données des premier et quatrième quartiles sont d’abord écartées, puis la moyenne arithmétique des deuxième et troisième quartiles de l’échantillon uniquement est calculée. La formule pour ce type de moyenne est donc :

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

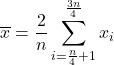
Enfin, vous pouvez également trouver la moyenne d’une fonction . La valeur moyenne d’une fonction continue sur un intervalle fermé [a,b] est calculée à l’aide de la formule suivante :

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Moyenne de l’échantillon et de la population

Enfin, nous allons voir quelle est la différence entre la moyenne de l’échantillon et la moyenne de la population, deux types de moyennes souvent confondues.

La moyenne de l’échantillon est la moyenne calculée sur les valeurs d’un échantillon statistique, c’est-à-dire qu’elle est calculée sur une partie de l’ensemble des valeurs d’une variable.

La moyenne de population est la moyenne calculée sur une population statistique, c’est-à-dire sur toutes les valeurs d’une variable. Par conséquent, la moyenne de la population coïncide avec l’espérance mathématique de la variable.

La moyenne de l’échantillon peut être considérée comme pratiquement égale à la moyenne de la population si un nombre suffisamment grand de données est connu. Mais la valeur de la moyenne de population est très difficile à obtenir, puisqu’en réalité toutes les valeurs d’une distribution sont rarement connues.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus