Comment calculer l’AIC dans SAS (avec exemple)

Le critère d’information d’Akaike (AIC) est une métrique utilisée pour comparer l’ajustement de plusieurs modèles de régression.

Il est calculé comme suit :

AIC = 2K – 2 ln (L)

où:

• K : Le nombre de paramètres du modèle. La valeur par défaut de K est 2, donc un modèle avec une seule variable prédictive aura une valeur K de 2+1 = 3.
• ln (L) : La log-vraisemblance du modèle. La plupart des logiciels statistiques peuvent calculer automatiquement cette valeur pour vous.

L’AIC est conçu pour trouver le modèle qui explique le plus de variation dans les données, tout en pénalisant les modèles qui utilisent un nombre excessif de paramètres.

Une fois que vous avez ajusté plusieurs modèles de régression, vous pouvez comparer la valeur AIC de chaque modèle. Plus l’AIC est bas, plus le modèle est adapté.

L’exemple suivant montre comment calculer l’AIC pour différents modèles de régression dans SAS.

Exemple : Comment calculer l’AIC dans SAS

Supposons que nous souhaitions adapter trois modèles de régression linéaire multiple différents pour prédire la note d’examen que les étudiants obtiendront dans une classe.

Voici les variables prédictives que nous utiliserons dans chaque modèle :

• Variables prédictives dans le modèle 1 : heures passées à étudier
• Variables prédictives dans le modèle 2 : examens pratiques passés
• Variables prédictives dans le modèle 3 : heures passées à étudier et examens pratiques passés

Tout d’abord, nous allons utiliser le code suivant pour créer un ensemble de données contenant ces informations pour 20 étudiants :

/*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run;

Ensuite, nous utiliserons proc reg pour ajuster chacun de ces modèles de régression et nous utiliserons l’instruction selection=adjrsq sse aic pour calculer les valeurs AIC pour chaque modèle :

/*fit multiple linear regression models and calculate AIC for each model*/
proc reg data=exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run;

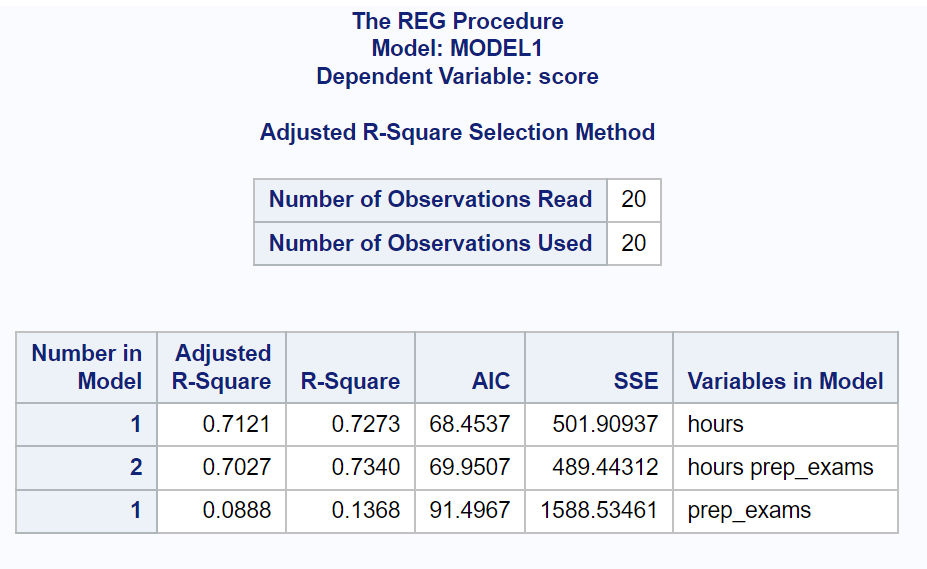
À partir du résultat, nous pouvons voir les valeurs AIC pour chaque modèle :

• AIC avec heures comme variable prédictive : 68,4537
• AIC avec heures et examens comme variables prédictives : 69,9507
• AIC avec examens comme variable prédictive : 91,4967

Le modèle avec la valeur AIC la plus basse est celui qui contient uniquement les heures comme variable prédictive.

Ainsi, nous déclarons que le modèle suivant est celui qui correspond le mieux aux données :

Score = β ₀ + β ₁ (heures étudiées)

Une fois que nous avons identifié ce modèle comme étant le meilleur, nous pouvons procéder à son ajustement et analyser les résultats, y compris la valeur R au carré et les coefficients bêta, pour déterminer la relation exacte entre les heures étudiées et la note de l’examen final.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment effectuer une régression linéaire simple dans SAS
Comment effectuer une régression linéaire multiple dans SAS
Comment calculer le R-carré dans SAS
Comment calculer le RMSE dans SAS