Ajustement de courbe en Python (avec exemples)

Souvent, vous souhaiterez peut-être ajuster une courbe à un ensemble de données en Python.

L’exemple étape par étape suivant explique comment ajuster les courbes aux données en Python à l’aide de la fonction numpy.polyfit() et comment déterminer quelle courbe correspond le mieux aux données.

Étape 1 : Créer et visualiser des données

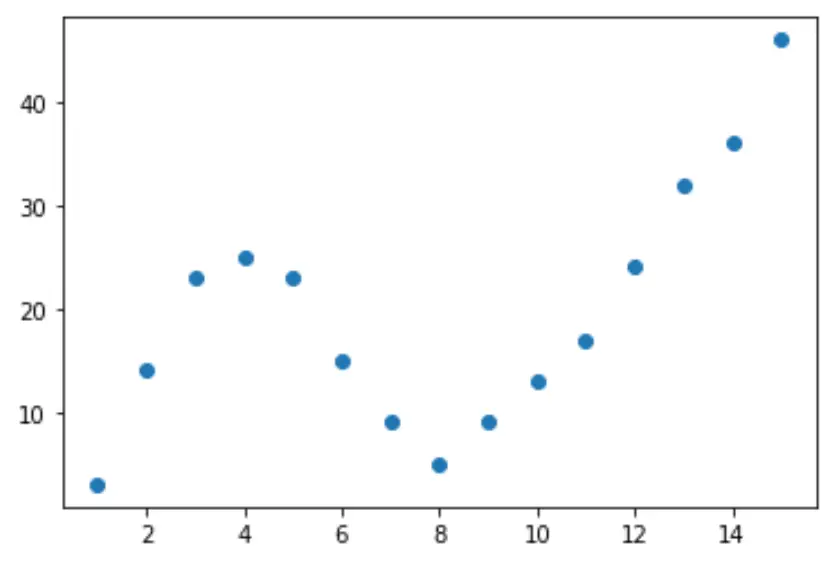
Commençons par créer un faux ensemble de données, puis créons un nuage de points pour visualiser les données :

import pandas as pd
import matplotlib.pyplot as plt

#create DataFrame
df = pd.DataFrame({'x': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   'y': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt.scatter(df.x, df.y)

Étape 2 : Ajuster plusieurs courbes

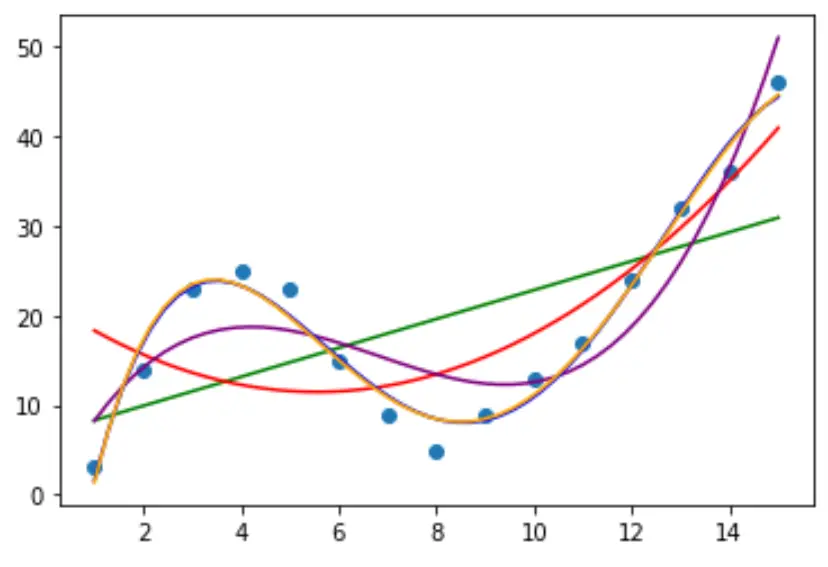
Ajustons ensuite plusieurs modèles de régression polynomiale aux données et visualisons la courbe de chaque modèle dans le même tracé :

import numpy as np

#fit polynomial models up to degree 5
model1 = np.poly1d(np.polyfit(df.x, df.y, 1))
model2 = np.poly1d(np.polyfit(df.x, df.y, 2))
model3 = np.poly1d(np.polyfit(df.x, df.y, 3))
model4 = np.poly1d(np.polyfit(df.x, df.y, 4))
model5 = np.poly1d(np.polyfit(df.x, df.y, 5))

#create scatterplot
polyline = np.linspace(1, 15, 50)
plt.scatter(df.x, df.y)

#add fitted polynomial lines to scatterplot 
plt.plot(polyline, model1(polyline), color='green')
plt.plot(polyline, model2(polyline), color='red')
plt.plot(polyline, model3(polyline), color='purple')
plt.plot(polyline, model4(polyline), color='blue')
plt.plot(polyline, model5(polyline), color='orange')
plt.show()

Pour déterminer quelle courbe correspond le mieux aux données, nous pouvons examiner le R carré ajusté de chaque modèle.

Cette valeur nous indique le pourcentage de variation de la variable de réponse qui peut être expliquée par la ou les variables prédictives du modèle, ajustées en fonction du nombre de variables prédictives.

#define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df.x, df.y, 1)
adjR(df.x, df.y, 2)
adjR(df.x, df.y, 3)
adjR(df.x, df.y, 4)
adjR(df.x, df.y, 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

À partir du résultat, nous pouvons voir que le modèle avec le R-carré ajusté le plus élevé est le polynôme du quatrième degré, qui a un R-carré ajusté de 0,959 .

Étape 3 : Visualisez la courbe finale

Enfin, nous pouvons créer un nuage de points avec la courbe du modèle polynomial du quatrième degré :

#fit fourth-degree polynomial
model4 = np.poly1d(np.polyfit(df.x, df.y, 4))

#define scatterplot
polyline = np.linspace(1, 15, 50)
plt.scatter(df.x, df.y)

#add fitted polynomial curve to scatterplot
plt.plot(polyline, model4(polyline), '--', color='red')
plt.show()

Nous pouvons également obtenir l’équation de cette ligne en utilisant la fonction print() :

print(model4)

          4          3         2
-0.01924 x + 0.7081 x - 8.365 x + 35.82 x - 26.52

L’équation de la courbe est la suivante :

y = -0,01924x ⁴ + 0,7081x ³ – 8,365x ² + 35,82x – 26,52

Nous pouvons utiliser cette équation pour prédire la valeur de la variable de réponse en fonction des variables prédictives du modèle. Par exemple si x = 4 alors nous prédirions que y = 23,32 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,365(4) ² + 35,82(4) – 26,52 = 23,32

Ressources additionnelles

Une introduction à la régression polynomiale
Comment effectuer une régression polynomiale en Python