Analyse discriminante linéaire dans R (étape par étape)

L’analyse discriminante linéaire est une méthode que vous pouvez utiliser lorsque vous disposez d’un ensemble de variables prédictives et que vous souhaitez classer une variable de réponse en deux classes ou plus.

Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une analyse discriminante linéaire dans R.

Étape 1 : Charger les bibliothèques nécessaires

Tout d’abord, nous allons charger les bibliothèques nécessaires pour cet exemple :

library(MASS)
library(ggplot2)

Étape 2 : Charger les données

Pour cet exemple, nous utiliserons l’ensemble de données iris intégré dans R. Le code suivant montre comment charger et afficher cet ensemble de données :

#attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame':	150 obs. of  5 variables:
 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

Nous pouvons voir que l’ensemble de données contient 5 variables et 150 observations au total.

Pour cet exemple, nous allons construire un modèle d’analyse discriminante linéaire pour classer à quelles espèces appartient une fleur donnée.

Nous utiliserons les variables prédictives suivantes dans le modèle :

• Sépale.longueur
• Sépale.Largeur
• Pétale.Longueur
• Pétale.Largeur

Et nous les utiliserons pour prédire la variable de réponse Species , qui prend en charge les trois classes potentielles suivantes :

• sétosa
• versicolor
• virginie

Étape 3 : mettre à l’échelle les données

L’une des hypothèses clés de l’analyse discriminante linéaire est que chacune des variables prédictives a la même variance. Un moyen simple de garantir que cette hypothèse est respectée consiste à mettre à l’échelle chaque variable de telle sorte qu’elle ait une moyenne de 0 et un écart type de 1.

Nous pouvons le faire rapidement dans R en utilisant la fonction scale() :

#scale each predictor variable (i.e. first 4 columns)
iris[1:4] <- scale(iris[1:4])

Nous pouvons utiliser la fonction apply() pour vérifier que chaque variable prédictive a désormais une moyenne de 0 et un écart type de 1 :

#find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length   Sepal.Width  Petal.Length   Petal.Width 
-4.484318e-16  2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
           1            1            1            1

Étape 4 : Créer des échantillons de formation et de test

Ensuite, nous diviserons l’ensemble de données en un ensemble d’entraînement sur lequel entraîner le modèle et un ensemble de test sur lequel tester le modèle :

#make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c(TRUE, FALSE), nrow(iris), replace=TRUE, prob=c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

Étape 5 : Ajuster le modèle LDA

Ensuite, nous utiliserons la fonction lda() du package MASS pour adapter le modèle LDA à nos données :

#fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor  virginica 
 0.3207547  0.3207547  0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa       -1.0397484   0.8131654   -1.2891006  -1.2570316
versicolor    0.1820921  -0.6038909    0.3403524   0.2208153
virginica     0.9582674  -0.1919146    1.0389776   1.1229172

Coefficients of linear discriminants:
                    LD1        LD2
Sepal.Length  0.7922820  0.5294210
Sepal.Width   0.5710586  0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width  -2.0602181  2.6326229

Proportion of trace:
   LD1    LD2 
0.9921 0.0079 

Voici comment interpréter les résultats du modèle :

Probabilités antérieures de groupe : celles-ci représentent les proportions de chaque espèce dans l’ensemble d’entraînement. Par exemple, 35,8 % de toutes les observations de l’ensemble d’entraînement concernaient l’espèce virginica .

Moyennes de groupe : elles affichent les valeurs moyennes de chaque variable prédictive pour chaque espèce.

Coefficients de discriminants linéaires : ceux-ci affichent la combinaison linéaire de variables prédictives utilisées pour former la règle de décision du modèle LDA. Par exemple:

• LD1 : 0,792 * longueur des sépales + 0,571 * largeur des sépales – 4,076 * longueur des pétales – 2,06 * largeur des pétales
• LD2 : 0,529 * longueur du sépale + 0,713 * largeur du sépale – 2,731 * longueur du pétale + 2,63 * largeur du pétale

Proportion de trace : ceux-ci affichent le pourcentage de séparation atteint par chaque fonction discriminante linéaire.

Étape 6 : Utiliser le modèle pour faire des prédictions

Une fois que nous avons ajusté le modèle à l’aide de nos données d’entraînement, nous pouvons l’utiliser pour faire des prédictions sur nos données de test :

#use LDA model to make predictions on test data
predicted <- predict(model, test)

names(predicted)

[1] "class"     "posterior" "x"   

Cela renvoie une liste avec trois variables :

• class : la classe prédite
• postérieur : Laprobabilité a posteriori qu’une observation appartienne à chaque classe
• x : Les discriminants linéaires

Nous pouvons visualiser rapidement chacun de ces résultats pour les six premières observations de notre ensemble de données de test :

#view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa   versicolor    virginica
4       1 2.425563e-17 1.341984e-35
6       1 1.400976e-21 4.482684e-40
7       1 3.345770e-19 1.511748e-37
15      1 6.389105e-31 7.361660e-53
17      1 1.193282e-25 2.238696e-45
18      1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1        LD2
4   7.150360 -0.7177382
6   7.961538  1.4839408
7   7.504033  0.2731178
15 10.170378  1.9859027
17  8.885168  2.1026494
18  8.113443  0.7563902

Nous pouvons utiliser le code suivant pour voir pour quel pourcentage d’observations le modèle LDA a correctement prédit l’espèce :

#find accuracy of model
mean(predicted$class==test$Species)

[1] 1

Il s’avère que le modèle a correctement prédit l’espèce pour 100 % des observations de notre ensemble de données de test.

Dans le monde réel, un modèle LDA prédit rarement correctement les résultats de chaque classe, mais cet ensemble de données sur l’iris est simplement construit de manière à ce que les algorithmes d’apprentissage automatique aient tendance à très bien fonctionner.

Étape 7 : Visualisez les résultats

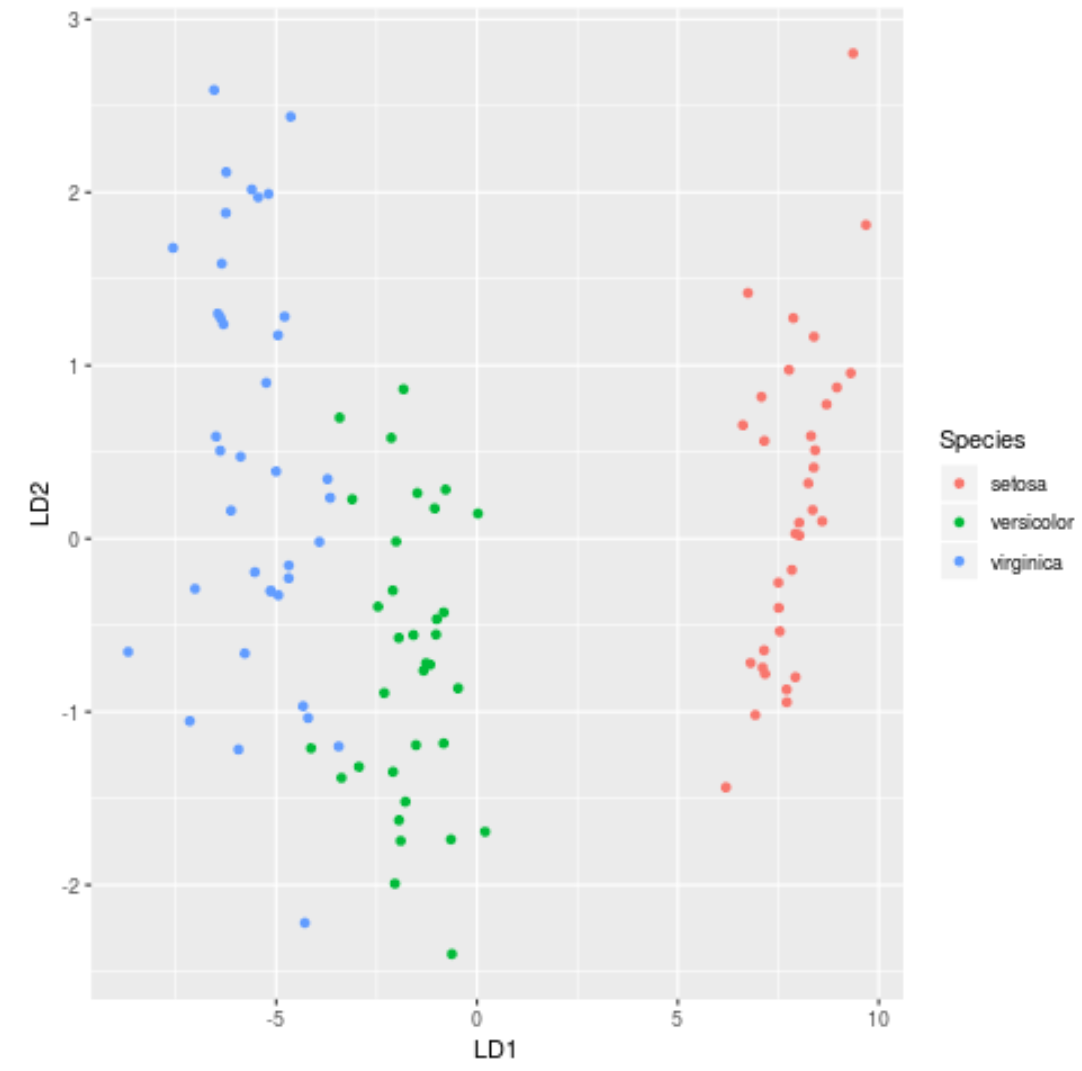
Enfin, nous pouvons créer un tracé LDA pour visualiser les discriminants linéaires du modèle et visualiser dans quelle mesure il sépare les trois espèces différentes dans notre ensemble de données :

#define data to plot
lda_plot <- cbind(train, predict(model)$x)

#create plot
ggplot(lda_plot, aes(LD1, LD2)) +
  geom_point(aes(color = Species))

Vous pouvez trouver le code R complet utilisé dans ce tutoriel ici .