Analyse des composantes principales dans R : exemple étape par étape

L’analyse en composantes principales, souvent abrégée PCA, est une technique d’apprentissage automatique non supervisée qui cherche à trouver les composantes principales – des combinaisons linéaires des prédicteurs d’origine – qui expliquent une grande partie de la variation dans un ensemble de données.

L’objectif de l’ACP est d’expliquer l’essentiel de la variabilité d’un ensemble de données avec moins de variables que l’ensemble de données d’origine.

Pour un ensemble de données donné avec p variables, nous pourrions examiner les nuages de points de chaque combinaison de variables par paire, mais le nombre de nuages de points peut devenir très rapidement important.

Pour p prédicteurs, il existe des nuages de points p(p-1)/2.

Ainsi, pour un ensemble de données avec p = 15 prédicteurs, il y aurait 105 nuages de points différents !

Heureusement, la PCA offre un moyen de trouver une représentation de faible dimension d’un ensemble de données qui capture autant que possible la variation des données.

Si nous parvenons à capturer l’essentiel de la variation dans seulement deux dimensions, nous pourrions projeter toutes les observations de l’ensemble de données d’origine sur un simple nuage de points.

La manière dont nous trouvons les composants principaux est la suivante :

Étant donné un ensemble de données avec p prédicteurs : X ₁ , X ₂ , … , X _p, , calculez Z ₁ , … , Z _M comme étant les M combinaisons linéaires des p prédicteurs d’origine où :

• Z _m = ΣΦ _jm X _j pour certaines constantes Φ _1m , Φ _2m , Φ _pm , m = 1, …, M.
• Z ₁ est la combinaison linéaire des prédicteurs qui capture le plus de variance possible.
• Z ₂ est la prochaine combinaison linéaire des prédicteurs qui capture le plus de variance tout en étant orthogonale (c’est-à-dire non corrélée) à Z ₁ .
• Z ₃ est alors la prochaine combinaison linéaire des prédicteurs qui capture le plus de variance tout en étant orthogonale à Z ₂ .
• Et ainsi de suite.

En pratique, nous utilisons les étapes suivantes pour calculer les combinaisons linéaires des prédicteurs originaux :

1. Mettez à l’échelle chacune des variables pour avoir une moyenne de 0 et un écart type de 1.

2. Calculez la matrice de covariance pour les variables mises à l’échelle.

3. Calculez les valeurs propres de la matrice de covariance.

En utilisant l’algèbre linéaire, on peut montrer que le vecteur propre qui correspond à la plus grande valeur propre est la première composante principale. En d’autres termes, cette combinaison particulière de prédicteurs explique la plus grande variance dans les données.

Le vecteur propre correspondant à la deuxième plus grande valeur propre est la deuxième composante principale, et ainsi de suite.

Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer ce processus dans R.

Étape 1 : Charger les données

Nous allons d’abord charger le package Tidyverse , qui contient plusieurs fonctions utiles pour visualiser et manipuler les données :

library(tidyverse)

Pour cet exemple, nous utiliserons l’ensemble de données USArrests intégré à R, qui contient le nombre d’arrestations pour 100 000 habitants dans chaque État américain en 1973 pour meurtre , agression et viol .

Il comprend également le pourcentage de la population de chaque État vivant dans des zones urbaines, UrbanPop .

Le code suivant montre comment charger et afficher les premières lignes de l’ensemble de données :

#load data
data("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama      13.2     236       58 21.2
Alaska       10.0     263       48 44.5
Arizona       8.1     294       80 31.0
Arkansas      8.8     190       50 19.5
California    9.0     276       91 40.6
Colorado      7.9     204       78 38.7

Étape 2 : Calculer les composantes principales

Après avoir chargé les données, nous pouvons utiliser la fonction intégrée de R prcomp() pour calculer les principales composantes de l’ensemble de données.

Assurez-vous de spécifier scale = TRUE afin que chacune des variables de l’ensemble de données soit mise à l’échelle pour avoir une moyenne de 0 et un écart type de 1 avant de calculer les composantes principales.

Notez également que les vecteurs propres dans R pointent dans le sens négatif par défaut, nous allons donc multiplier par -1 pour inverser les signes.

#calculate principal components
results <- prcomp(USArrests, scale = TRUE)

#reverse the signs
results$rotation <- -1*results$rotation

#display principal components
results$rotation

               PC1        PC2        PC3         PC4
Murder   0.5358995 -0.4181809  0.3412327 -0.64922780
Assault  0.5831836 -0.1879856  0.2681484  0.74340748
UrbanPop 0.2781909  0.8728062  0.3780158 -0.13387773
Rape     0.5434321  0.1673186 -0.8177779 -0.08902432

Nous pouvons voir que la première composante principale (PC1) a des valeurs élevées pour le meurtre, l’agression et le viol, ce qui indique que cette composante principale décrit la plus grande variation de ces variables.

Nous pouvons également voir que la deuxième composante principale (PC2) a une valeur élevée pour UrbanPop, ce qui indique que cette composante principale met l’accent sur la population urbaine.

Notez que les scores des composants principaux pour chaque état sont stockés dans results$x . On multipliera également ces scores par -1 pour inverser les signes :

#reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1        PC2         PC3          PC4
Alabama     0.9756604 -1.1220012  0.43980366 -0.154696581
Alaska      1.9305379 -1.0624269 -2.01950027  0.434175454
Arizona     1.7454429  0.7384595 -0.05423025  0.826264240
Arkansas   -0.1399989 -1.1085423 -0.11342217  0.180973554
California  2.4986128  1.5274267 -0.59254100  0.338559240
Colorado    1.4993407  0.9776297 -1.08400162 -0.001450164

Étape 3 : Visualisez les résultats avec un biplot

Ensuite, nous pouvons créer un biplot – un tracé qui projette chacune des observations de l’ensemble de données sur un nuage de points qui utilise les première et deuxième composantes principales comme axes :

Notez que scale = 0 garantit que les flèches du tracé sont mises à l’échelle pour représenter les chargements.

biplot(results, scale = 0)

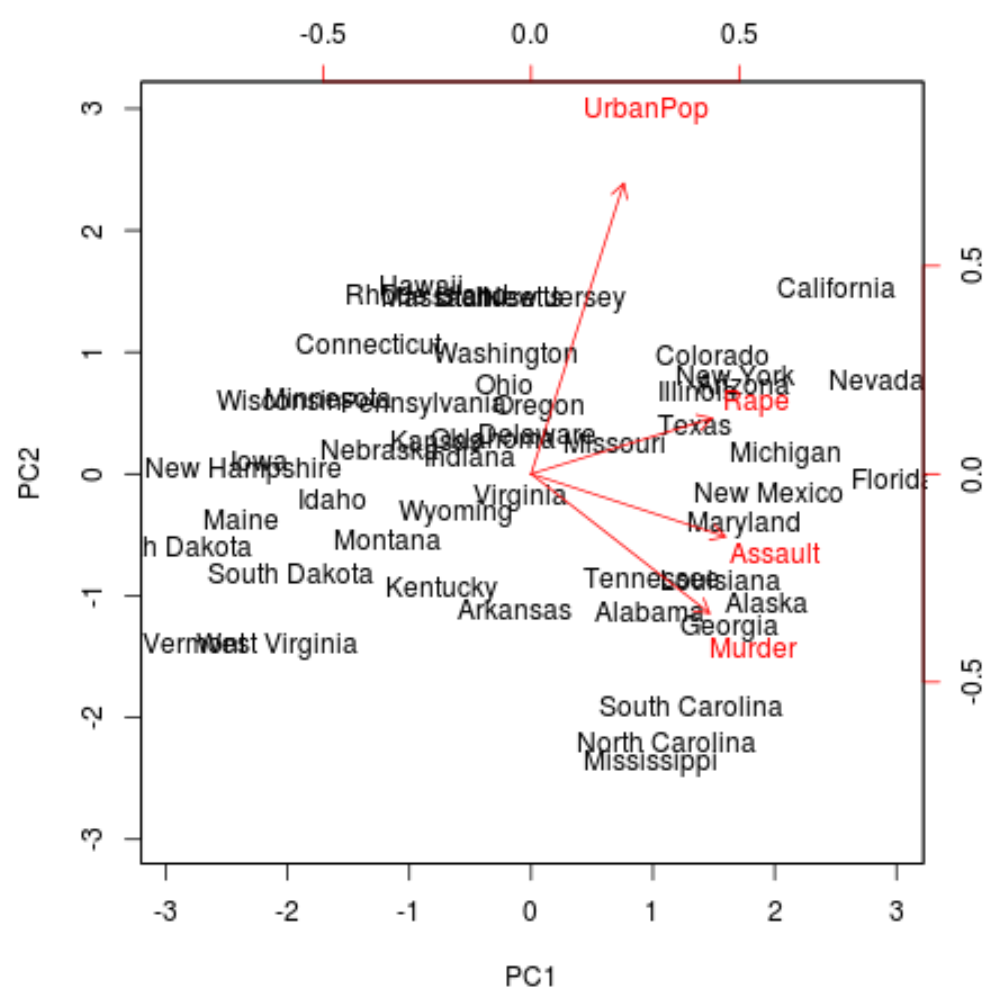
À partir du tracé, nous pouvons voir chacun des 50 états représentés dans un espace simple à deux dimensions.

Les États proches les uns des autres sur le graphique ont des modèles de données similaires en ce qui concerne les variables de l’ensemble de données d’origine.

Nous pouvons également constater que certains États sont plus fortement associés à certains crimes qu’à d’autres. Par exemple, la Géorgie est l’État le plus proche de la variable Meurtre dans l’intrigue.

Si nous examinons les États ayant les taux de meurtres les plus élevés dans l’ensemble de données d’origine, nous pouvons voir que la Géorgie est en fait en tête de liste :

#display states with highest murder rates in original dataset
head(USArrests[order(-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia          17.4     211       60 25.8
Mississippi      16.1     259       44 17.1
Florida          15.4     335       80 31.9
Louisiana        15.4     249       66 22.2
South Carolina   14.4     279       48 22.5
Alabama          13.2     236       58 21.2

Étape 4 : Trouver l’écart expliqué par chaque composante principale

Nous pouvons utiliser le code suivant pour calculer la variance totale dans l’ensemble de données d’origine expliquée par chaque composante principale :

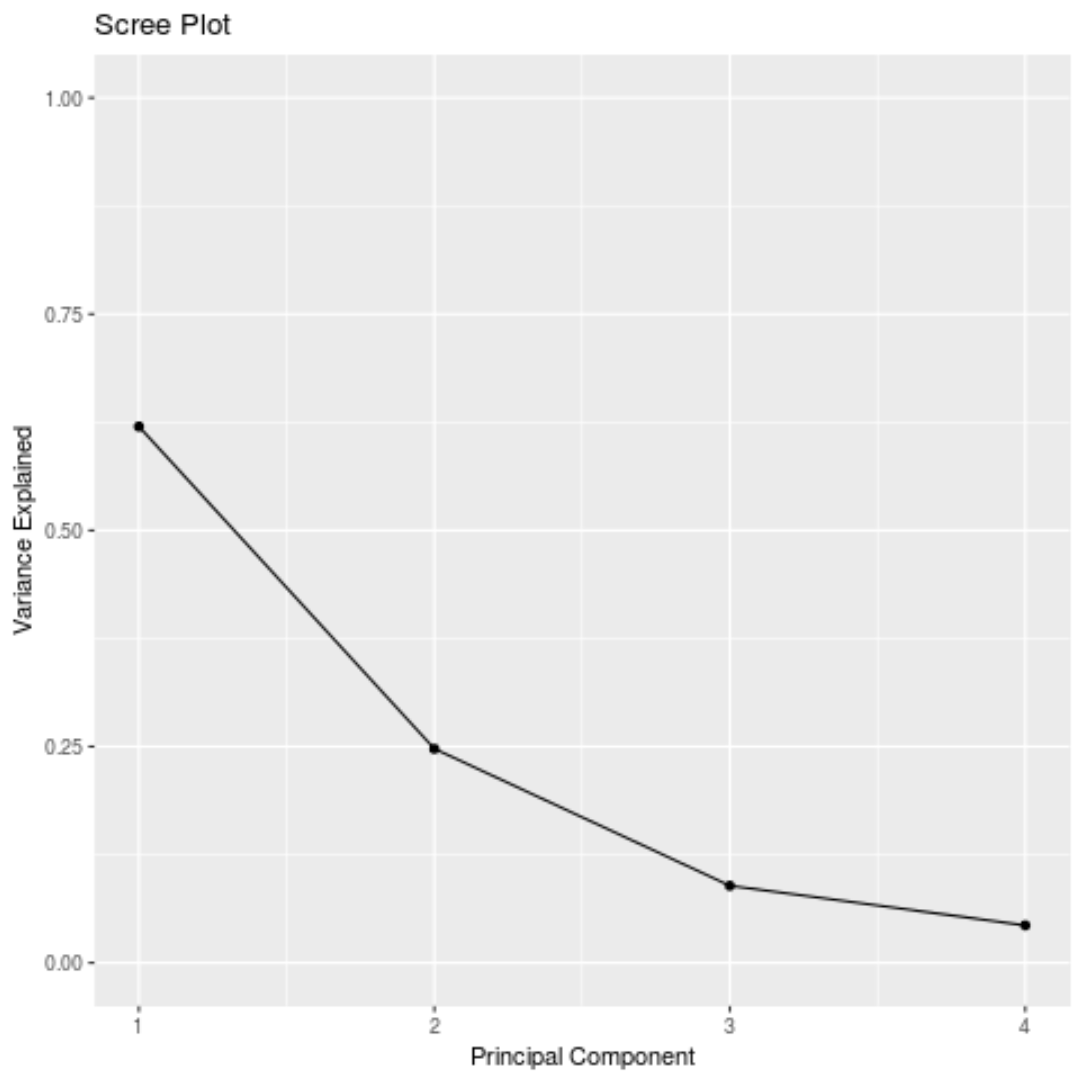
#calculate total variance explained by each principal component
results$sdev^2 / sum(results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

A partir des résultats, nous pouvons observer ce qui suit :

• La première composante principale explique 62 % de la variance totale de l’ensemble de données.
• La deuxième composante principale explique 24,7 % de la variance totale de l’ensemble de données.
• La troisième composante principale explique 8,9 % de la variance totale de l’ensemble de données.
• La quatrième composante principale explique 4,3 % de la variance totale de l’ensemble de données.

Ainsi, les deux premières composantes principales expliquent la majorité de la variance totale des données.

C’est un bon signe car le biplot précédent projetait chacune des observations des données originales sur un nuage de points qui ne prenait en compte que les deux premières composantes principales.

Ainsi, il est valable d’examiner les modèles dans le biplot pour identifier les états similaires les uns aux autres.

Nous pouvons également créer un graphique d’éboulis – un graphique qui affiche la variance totale expliquée par chaque composante principale – pour visualiser les résultats de l’ACP :

#calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum(results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab("Principal Component") + 
  ylab("Variance Explained") +
  ggtitle("Scree Plot") +
  ylim(0, 1)

Analyse en composantes principales en pratique

En pratique, la PCA est utilisée le plus souvent pour deux raisons :

1. Analyse exploratoire des données – Nous utilisons l’ACP lorsque nous explorons pour la première fois un ensemble de données et que nous voulons comprendre quelles observations dans les données sont les plus similaires les unes aux autres.

2. Régression des composantes principales – Nous pouvons également utiliser l’ACP pour calculer les composantes principales qui peuvent ensuite être utilisées dans la régression des composantes principales . Ce type de régression est souvent utilisé lorsqu’il existe une multicolinéarité entre les prédicteurs d’un ensemble de données.

Le code R complet utilisé dans ce tutoriel peut être trouvé ici .