Une introduction à ANCOVA (analyse de variance)

ANCOVA signifie « analyse de covariance ». Pour comprendre le fonctionnement d’une ANCOVA, il est utile de d’abord comprendre l’ANOVA.

Une ANOVA   (analyse de variance) est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Par exemple, supposons que nous voulions savoir si la technique d’étude a ou non un impact sur les résultats aux examens d’une classe d’étudiants. Nous avons divisé la classe en trois groupes au hasard. Chaque groupe utilise une technique d’étude différente pendant un mois pour préparer un examen. A la fin du mois, tous les étudiants passent le même examen.

Pour savoir si l’étude de la technique a un impact sur les résultats aux examens, nous pouvons effectuer une ANOVA unidirectionnelle, qui nous dira s’il existe une différence statistiquement significative entre les scores moyens des trois groupes.

Une ANCOVA est une extension d’une ANOVA dans laquelle nous souhaitons déterminer s’il existe une différence statistiquement significative entre trois groupes indépendants ou plus après avoir pris en compte une ou plusieurs covariables .

Une covariable est une variable continue qui varie avec la variable de réponse.

Par exemple, supposons que nous voulions savoir si la technique d’étude a ou non un impact sur les résultats aux examens, mais que nous voulions tenir compte de la note que l’élève a déjà dans la classe . Nous pouvons utiliser leur note actuelle comme covariable et effectuer une ANCOVA pour déterminer s’il existe une différence statistiquement significative entre les résultats moyens aux examens des trois groupes.

Cela nous permet de tester si la technique d’étude a ou non un impact sur les résultats aux examens une fois l’influence de la covariable supprimée.

Ainsi, si nous constatons qu’il existe une différence statistiquement significative dans les résultats aux examens entre les trois techniques d’étude, nous pouvons être sûrs que cette différence existe même après avoir pris en compte la note actuelle des élèves dans la classe (c’est-à-dire s’ils réussissent déjà bien ou s’ils réussissent déjà bien). pas en classe) .

Hypothèses de l’ANCOVA

Avant d’effectuer une ANCOVA, il est important de s’assurer que les hypothèses suivantes sont respectées :

• La ou les covariables et la ou les variables factorielles sont indépendantes – La covariable et la variable factorielle doivent être indépendantes l’une de l’autre, car l’ajout d’un terme covariable dans le modèle n’a de sens que si la covariable et la variable factorielle agissent indépendamment sur le variable de réponse.
• La ou les covariables sont des données continues. Les covariables doivent être continues (c’est-à-dire des données d’intervalle ou de rapport ).
• Homogénéité des variances – Les variances entre les groupes doivent être à peu près égales.
• Indépendance – Les observations dans chaque groupe doivent être indépendantes.
• Normalité – Les données doivent être réparties à peu près normalement dans chaque groupe.
• Pas de valeurs aberrantes extrêmes – Il ne devrait y avoir aucune valeur aberrante extrême dans aucun des groupes qui pourrait affecter de manière significative les résultats de l’ANCOVA.

ANCOVA : exemple

Une enseignante souhaite savoir si trois techniques d’étude différentes ont un impact sur les résultats des examens, mais elle souhaite tenir compte de la note actuelle que l’élève a déjà dans la classe.

Elle effectuera une ANCOVA en utilisant les variables suivantes :

• Variable factorielle : technique d’étude
• Covariable : note actuelle
• Variable de réponse : score à l’examen

Le tableau suivant présente l’ensemble de données des 15 étudiants recrutés pour participer à l’étude :

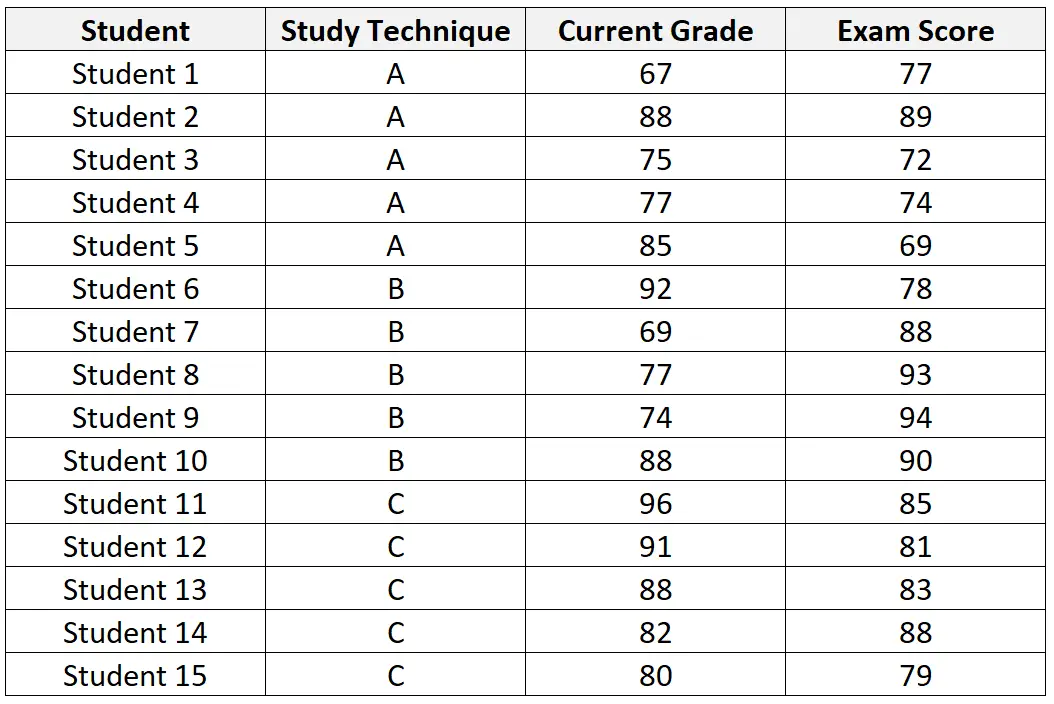
Après avoir effectué une ANCOVA sur l’ensemble de données, l’enseignant obtient les résultats suivants :

La valeur p pour la technique d’étude est de 0,03155 . Puisque cette valeur est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle selon laquelle chacune des techniques d’étude conduit à la même note moyenne à l’examen, même après avoir pris en compte la note actuelle de l’étudiant dans la classe .

Pour déterminer exactement quelles techniques d’étude produisent des résultats moyens différents aux examens, l’enseignant devra effectuer des tests post-hoc .

Ressources additionnelles

Comment effectuer une ANCOVA dans Excel
Comment effectuer une ANCOVA dans R
Comment effectuer une ANCOVA en Python
Les différences entre ANOVA, ANCOVA, MANOVA et MANCOVA