Comment effectuer une ANOVA imbriquée dans R (étape par étape)

Une ANOVA imbriquée est un type d’ANOVA (« analyse de variance ») dans laquelle au moins un facteur est imbriqué dans un autre facteur.

Par exemple, supposons qu’un chercheur veuille savoir si trois engrais différents produisent différents niveaux de croissance des plantes.

Pour tester cela, trois techniciens différents saupoudrent chacun l’engrais A sur quatre plantes, trois autres techniciens saupoudrent chacun l’engrais B sur quatre plantes et trois autres techniciens saupoudrent chacun l’engrais C sur quatre plantes.

Dans ce scénario, la variable de réponse est la croissance des plantes et les deux facteurs sont le technicien et l’engrais. Il s’avère que le technicien est niché dans l’engrais :

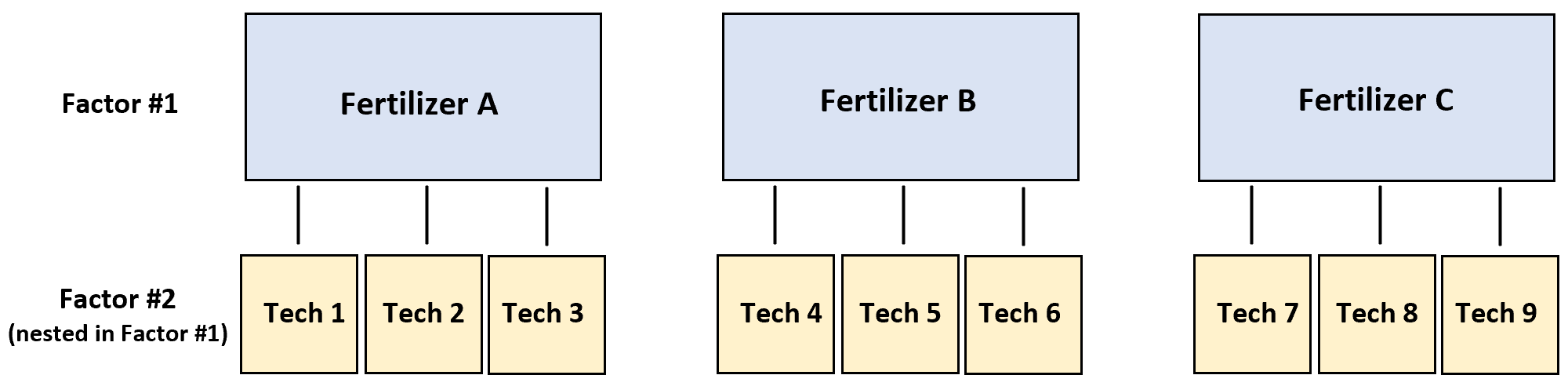
L’exemple étape par étape suivant montre comment effectuer cette ANOVA imbriquée dans R.

Étape 1 : Créer les données

Tout d’abord, créons un bloc de données pour contenir nos données dans R :

#create data
df <- data.frame(growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c('A', 'B', 'C'), each=12)),
                 tech=c(rep(1:9, each=4)))

#view first six rows of data
head(df)

  growth fertilizer tech
1     13          A    1
2     16          A    1
3     16          A    1
4     12          A    1
5     15          A    2
6     16          A    2

Étape 2 : Ajuster l’ANOVA imbriquée

Nous pouvons utiliser la syntaxe suivante pour ajuster une ANOVA imbriquée dans R :

aov(réponse ~ facteur A / facteur B)

où:

• réponse : la variable de réponse
• facteur A : le premier facteur
• facteur B : le deuxième facteur imbriqué dans le premier facteur

Le code suivant montre comment ajuster l’ANOVA imbriquée pour notre ensemble de données :

#fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value   Pr(>F)    
df$fertilizer                  2  372.7  186.33  53.238 4.27e-10 ***
df$fertilizer:factor(df$tech)  6   31.8    5.31   1.516    0.211    
Residuals                     27   94.5    3.50                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Étape 3 : Interpréter le résultat

Nous pouvons consulter la colonne de valeur p pour déterminer si chaque facteur a ou non un effet statistiquement significatif sur la croissance des plantes.

D’après le tableau ci-dessus, nous pouvons voir que l’engrais a un effet statistiquement significatif sur la croissance des plantes (valeur p < 0,05), mais pas le technicien (valeur p = 0,211).

Cela nous indique que si nous souhaitons augmenter la croissance des plantes, nous devons nous concentrer sur l’engrais utilisé plutôt que sur le technicien individuel qui épand l’engrais.

Étape 4 : Visualisez les résultats

Enfin, on peut utiliser des boxplots pour visualiser la répartition de la croissance des plantes par engrais et par technicien :

#load ggplot2 data visualization package
library(ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes(x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

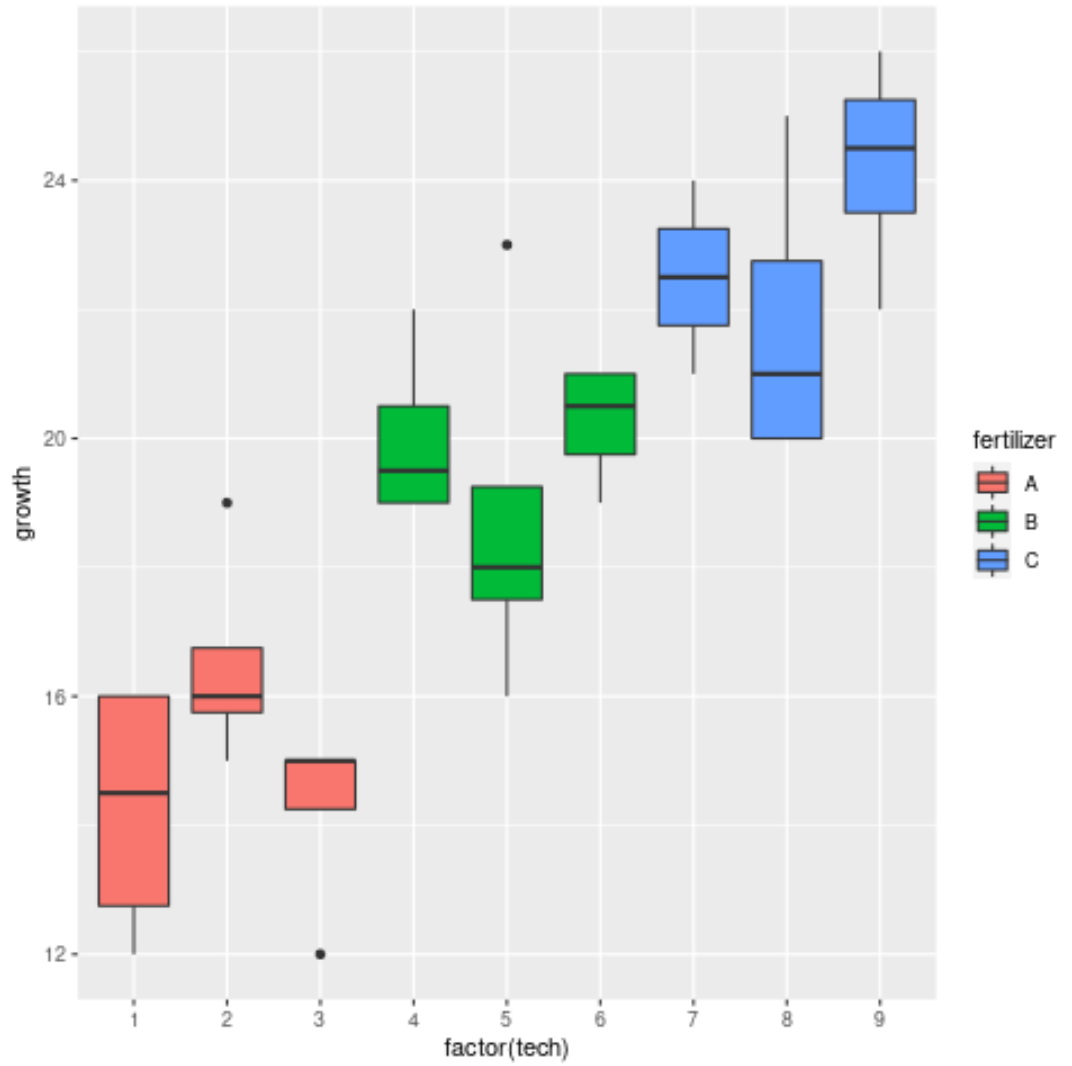
Le graphique montre qu’il existe une variation significative de la croissance entre les trois différents engrais, mais pas autant de variation entre les techniciens au sein de chaque groupe d’engrais.

Cela semble correspondre aux résultats de l’ANOVA emboîtée et confirme que les engrais ont un effet significatif sur la croissance des plantes, mais pas les techniciens individuels.

Ressources additionnelles

Comment effectuer une ANOVA unidirectionnelle dans R
Comment effectuer une ANOVA bidirectionnelle dans R
Comment effectuer une ANOVA à mesures répétées dans R