Comment effectuer une ANOVA avec des tailles d’échantillon inégales

Une question que les étudiants se posent souvent en matière de statistiques est la suivante :

Est-il possible d’effectuer une ANOVA unidirectionnelle lorsque les tailles d’échantillon de chaque groupe ne sont pas égales ?

La réponse courte :

Oui, vous pouvez effectuer une ANOVA unidirectionnelle lorsque les tailles d’échantillon ne sont pas égales. Des tailles d’échantillon égales ne font pas partie des hypothèses formulées dans une ANOVA.

Cependant, il y a deux problèmes potentiels à prendre en compte lors de la réalisation d’une ANOVA unidirectionnelle avec des tailles d’échantillon inégales :

(1) Puissance statistique réduite.

(2) Robustesse réduite à une variance inégale.

Les sections suivantes expliquent en détail ces deux problèmes potentiels.

Problème n°1 : puissance statistique réduite

Lorsque nous utilisons n’importe quel type de test statistique pour comparer des groupes, la puissance statistique du test est la plus élevée lorsque chaque groupe a une taille d’échantillon égale.

Rappelons que la puissance statistique fait référence à la probabilité qu’un test détecte un effet alors qu’il y en a réellement un.

On peut montrer que plus les différences de taille d’échantillon entre les groupes sont grandes, plus la puissance statistique d’une ANOVA est faible.

C’est pourquoi les chercheurs souhaitent généralement des tailles d’échantillon égales afin d’avoir une puissance plus élevée et donc une plus grande probabilité de détecter de véritables différences.

Il est certainement possible d’effectuer une ANOVA unidirectionnelle avec des tailles d’échantillon inégales, mais vous devez être conscient que la puissance de l’ANOVA unidirectionnelle sera réduite.

Problème n°2 : Robustesse réduite à une variance inégale

L’une des hypothèses d’une ANOVA unidirectionnelle est que la variance entre chaque groupe est égale.

En général, une ANOVA unidirectionnelle est considérée comme robuste aux violations de l’hypothèse des variances égales, mais seulement si chaque groupe a la même taille d’échantillon .

Ainsi, si vous avez des tailles d’échantillon inégales et des variances inégales entre les groupes, alors les résultats de l’ANOVA unidirectionnelle peuvent être difficiles à faire confiance.

Comment décider d’utiliser une ANOVA unidirectionnelle avec des tailles d’échantillon inégales

Si vous avez des tailles d’échantillon inégales et que vous souhaitez effectuer une ANOVA unidirectionnelle pour tester les différences entre les moyennes des groupes, vous pouvez utiliser l’organigramme suivant pour décider comment procéder :

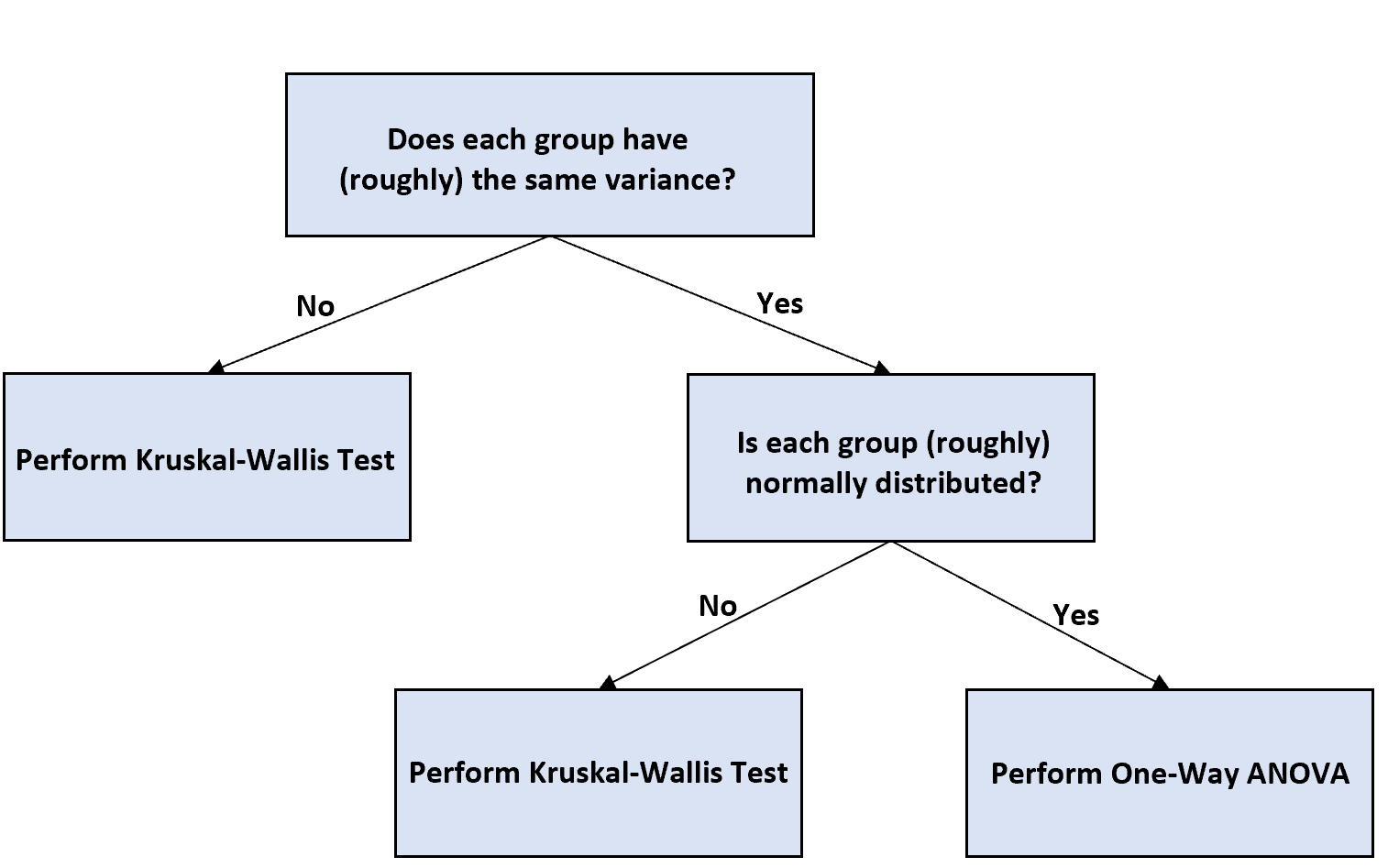
Voici une brève explication de l’organigramme :

Étape 1 : Déterminez si chaque groupe a la même variance.

Pour déterminer si chaque groupe présente la même variance, vous pouvez utiliser l’une des deux approches suivantes :

• Créez des boîtes à moustaches pour chaque groupe et voyez si la répartition des valeurs dans chaque groupe est à peu près égale.
• Effectuez un test statistique formel pour des variances égales comme le test de Bartlett .

Si les variances ne sont pas égales, effectuez un test de Kruskal-Wallis , qui est considéré comme l’équivalent non paramétrique d’une ANOVA unidirectionnelle.

Si les écarts sont égaux, passez à l’étape suivante.

Étape 2 : Déterminez si chaque groupe est normalement distribué.

Pour déterminer si les valeurs de chaque groupe sont à peu près normalement distribuées, vous pouvez utiliser l’une des deux approches suivantes :

• Créez des histogrammes ou des tracés QQ pour chaque groupe.
• Effectuez des tests statistiques formels comme Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre ou D’Agostino-Pearson.

Si chaque groupe est normalement distribué, vous pouvez procéder à une ANOVA unidirectionnelle et interpréter les résultats comme vous le feriez avec n’importe quelle ANOVA unidirectionnelle ordinaire.

Si chaque groupe n’est pas distribué normalement, effectuez plutôt un test de Kruskal-Wallis.

Ressources additionnelles

Une introduction à l’ANOVA unidirectionnelle
Comment vérifier les hypothèses de l’ANOVA
Une introduction au test de Kruskal-Wallis
Comment interpréter la valeur F et la valeur P dans l’ANOVA