Comment effectuer un test t pour échantillons appariés dans Excel

Un test t pour échantillons appariés est utilisé pour comparer les moyennes de deux échantillons lorsque chaque observation dans un échantillon peut être associée à une observation dans l’autre échantillon.

Ce didacticiel explique comment effectuer un test t pour échantillons appariés dans Excel.

Comment effectuer un test t pour échantillons appariés dans Excel

Supposons que nous voulions savoir si un certain programme d’études a un impact significatif sur les performances des étudiants à un examen particulier. Pour tester cela, nous demandons à 20 élèves d’une classe de passer un pré-test. Ensuite, nous faisons participer chacun des étudiants au programme d’études pendant deux semaines. Ensuite, les étudiants repassent un test de difficulté similaire.

Pour comparer la différence entre les scores moyens au premier et au deuxième test, nous utilisons un test t pour échantillons appariés car pour chaque élève, son score au premier test peut être associé à son score au deuxième test.

L’image suivante montre le score pré-test et le score post-test de chaque élève :

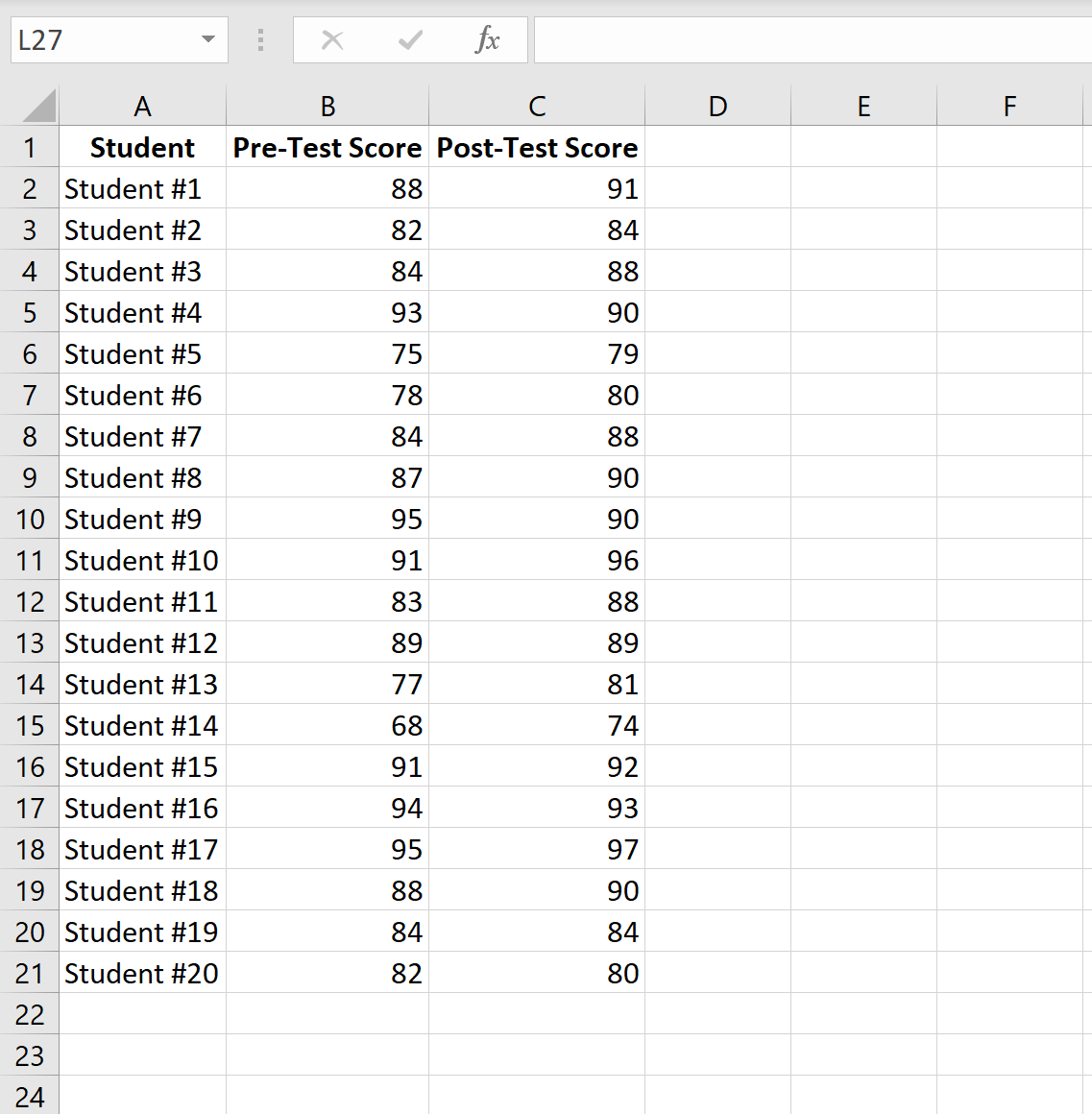
Effectuez les étapes suivantes pour effectuer un test t sur échantillons appariés afin de déterminer s’il existe une différence significative dans les résultats moyens du test entre le pré-test et le post-test.

Étape 1 : Ouvrez le ToolPak d’analyse des données.

Dans l’onglet Données du ruban supérieur, cliquez sur « Analyse des données ».

Si vous ne voyez pas cette option sur laquelle cliquer, vous devez d’abord télécharger le Analysis ToolPak , qui est entièrement gratuit.

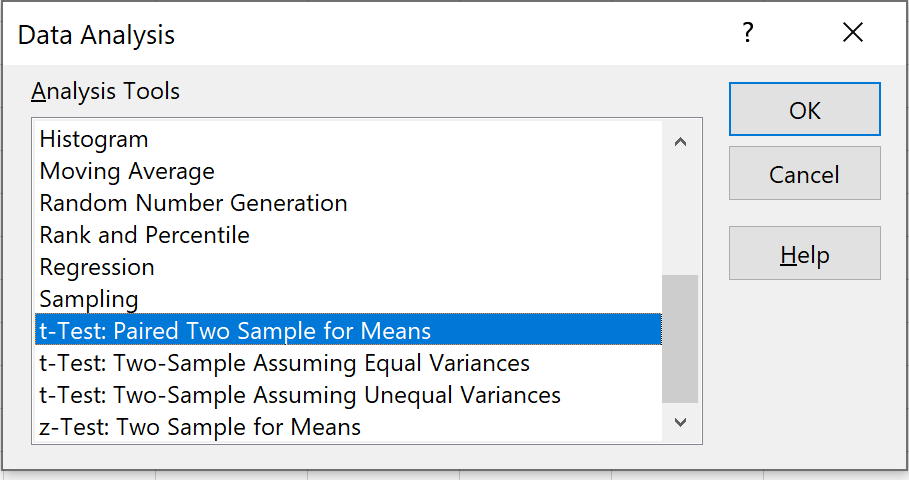
Étape 2 : Sélectionnez le test approprié à utiliser.

Sélectionnez l’option qui dit T-Test : Paired Two Sample for Means , puis cliquez sur OK.

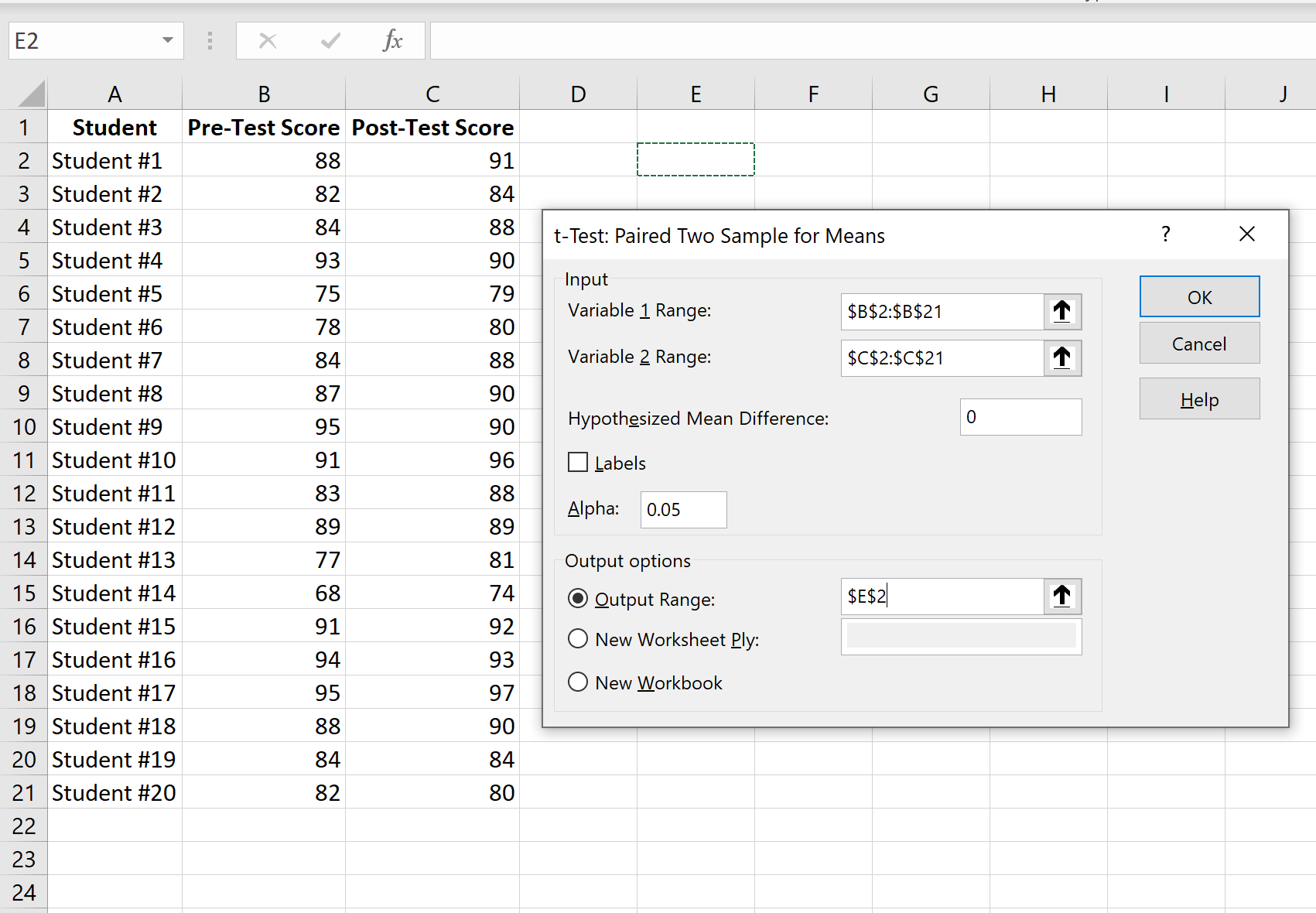
Étape 3 : Saisissez les informations nécessaires.

Entrez la plage de valeurs pour la variable 1 (les scores pré-test), la variable 2 (les scores post-test), la différence moyenne hypothétique (dans ce cas, nous mettons « 0 » car nous voulons savoir si la véritable différence moyenne entre les scores pré-test et post-test sont 0), et la plage de sortie dans laquelle nous aimerions voir les résultats du test affichés. Ensuite, cliquez sur OK.

Étape 4 : Interprétez les résultats.

Une fois que vous avez cliqué sur OK à l’étape précédente, les résultats du test t seront affichés.

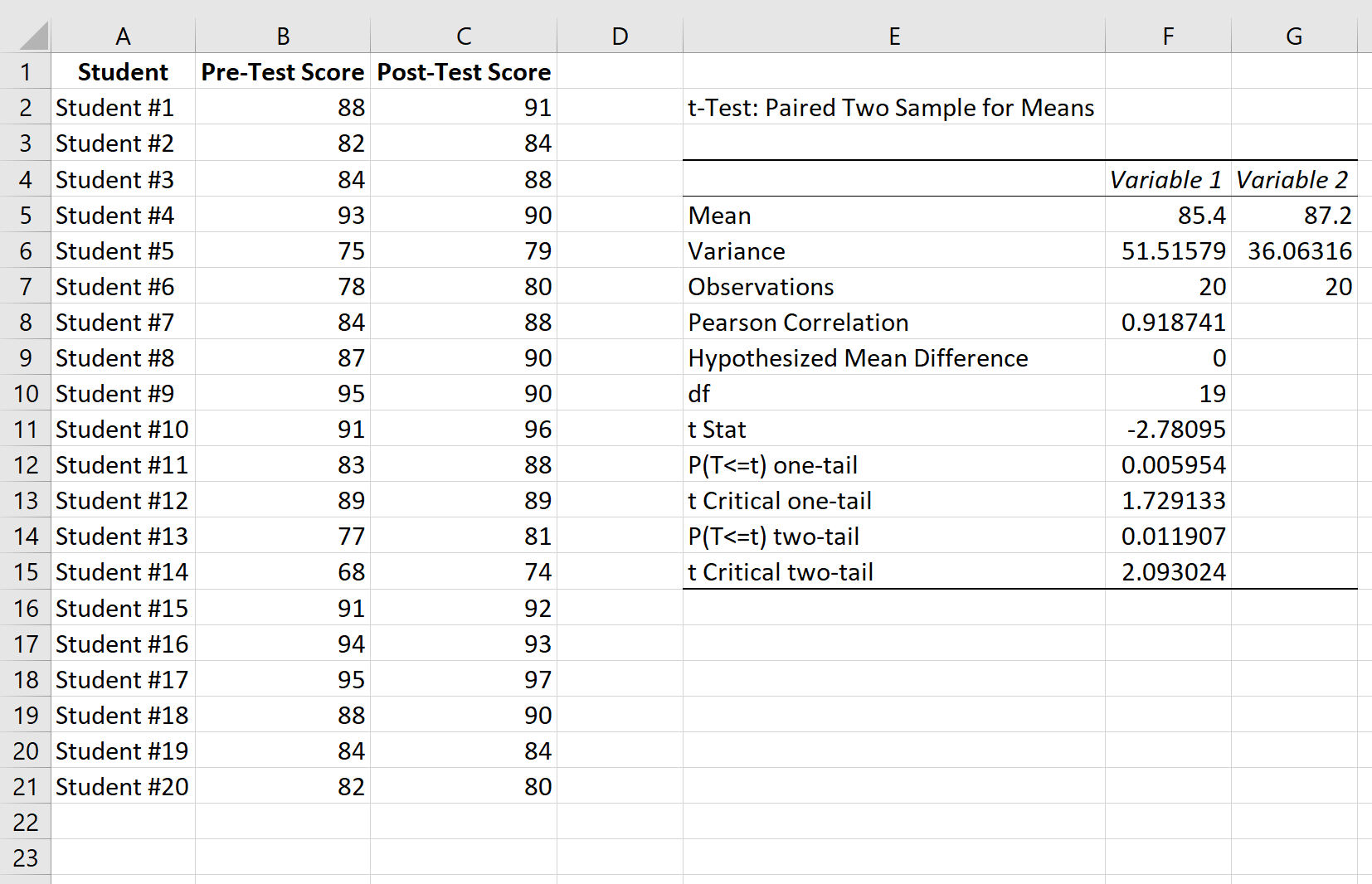
Voici comment interpréter les résultats :

Moyenne : Il s’agit de la moyenne de chaque échantillon. Le score moyen pré-test est de 85,4 et le score moyen post-test est de 87,2 .

Variance : Il s’agit de la variance pour chaque échantillon. La variance des scores pré-test est de 51,51 et la variance des scores post-test est de 36,06 .

Observations : Il s’agit du nombre d’observations dans chaque échantillon. Les deux échantillons contiennent 20 observations.

Corrélation de Pearson : La corrélation entre les scores pré-test et les scores post-test. Il s’avère que c’est 0,918 .

Différence moyenne hypothétique : le nombre sur lequel nous « émettons l’hypothèse » est la différence entre les deux moyennes. Dans ce cas, nous avons choisi 0 car nous voulons tester s’il existe ou non une différence entre les scores pré-test et post-test.

df : Les degrés de liberté pour le test t. Ceci est calculé comme n-1 où n est le nombre de paires. Dans ce cas, df = 20 – 1 = 19 .

t Stat : La statistique de test t , qui s’avère être -2,78 .

P(T<=t) bilatéral : la valeur p pour un test t bilatéral. Dans ce cas, p = 0,011907 . C’est plus petit que alpha = 0,05, nous rejetons donc l’hypothèse nulle. Nous disposons de suffisamment de preuves pour affirmer qu’il existe une différence statistiquement significative entre le score moyen pré-test et post-test.

t Critique bilatéral : Il s’agit de la valeur critique du test, trouvée en identifiant la valeur dans le tableau de distribution t qui correspond à un test bilatéral avec alpha = 0,05 et df = 19. Cela s’avère être 2,093024 . Puisque la valeur absolue de notre statistique de test t est supérieure à cette valeur, nous rejetons l’hypothèse nulle. Nous disposons de suffisamment de preuves pour affirmer qu’il existe une différence statistiquement significative entre le score moyen pré-test et post-test.

Notez que l’approche de la valeur p et de la valeur critique conduira toutes deux à la même conclusion.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tests t dans Excel :

Comment effectuer un test t sur un échantillon dans Excel
Comment effectuer un test t à deux échantillons dans Excel