Une introduction aux arbres de classification et de régression

Lorsque la relation entre un ensemble de variables prédictives et une variable de réponse est linéaire, des méthodes telles que la régression linéaire multiple peuvent produire des modèles prédictifs précis.

Cependant, lorsque la relation entre un ensemble de prédicteurs et une réponse est hautement non linéaire et complexe, les méthodes non linéaires peuvent alors donner de meilleurs résultats.

Un exemple de méthode non linéaire est celui des arbres de classification et de régression , souvent abrégés CART .

Comme leur nom l’indique, les modèles CART utilisent un ensemble de variables prédictives pour créer des arbres de décision qui prédisent la valeur d’une variable de réponse.

Par exemple, supposons que nous ayons un ensemble de données contenant les variables prédictives Années de jeu et circuits moyens ainsi que la variable de réponse Salaire annuel pour des centaines de joueurs de baseball professionnels.

Voici à quoi pourrait ressembler un arbre de régression pour cet ensemble de données :

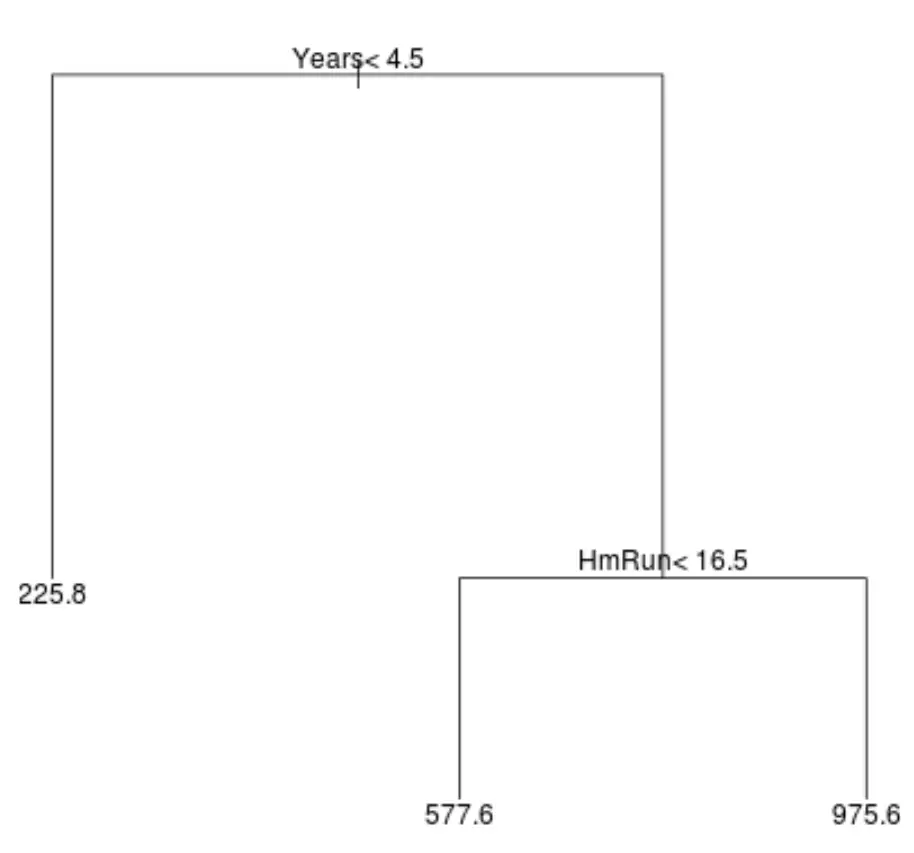
La façon d’interpréter l’arbre est la suivante :

• Les joueurs ayant joué moins de 4,5 ans ont un salaire prévu de 225,8 000 $.
• Les joueurs ayant joué plus de 4,5 ans ou plus et moins de 16,5 circuits en moyenne ont un salaire prévu de 577,6 000 $.
• Les joueurs avec une expérience de jeu supérieure ou égale à 4,5 ans et une moyenne supérieure ou égale à 16,5 circuits ont un salaire prévu de 975,6 000 $.

Les résultats de ce modèle devraient intuitivement avoir un sens : les joueurs avec plus d’années d’expérience et plus de circuits moyens ont tendance à gagner des salaires plus élevés.

On peut alors utiliser ce modèle pour prédire le salaire d’un nouveau joueur.

Par exemple, supposons qu’un joueur donné ait joué 8 ans et réalise en moyenne 10 circuits par an. Selon notre modèle, nous prédirions que ce joueur a un salaire annuel de 577,6k$.

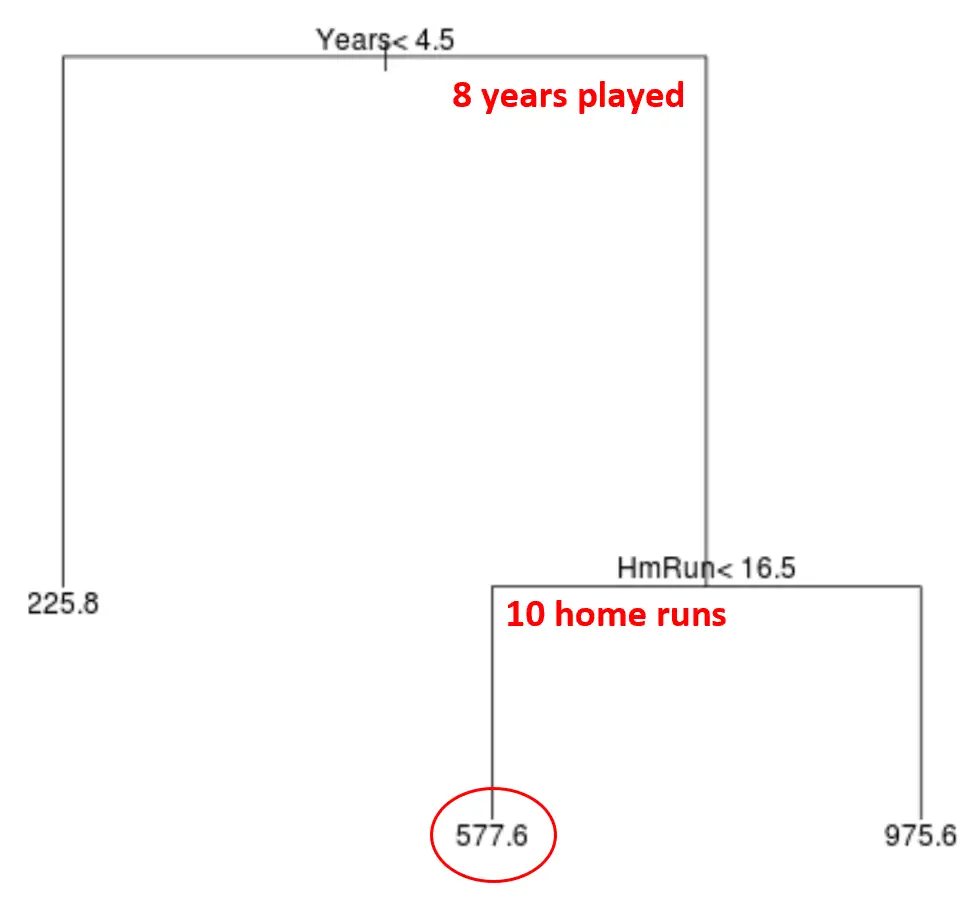
Quelques remarques sur l’arbre :

• La première variable prédictive située en haut de l’arbre est la plus importante, c’est-à-dire celle qui influe le plus sur la prédiction de la valeur de la variable réponse. Dans ce cas, les années jouées permettent de mieux prédire le salaire que la moyenne des circuits .
• Les régions situées au bas de l’arborescence sont appelées nœuds terminaux . Cet arbre particulier a trois nœuds terminaux.

Étapes pour créer des modèles CART

Nous pouvons utiliser les étapes suivantes pour créer un modèle CART pour un ensemble de données donné :

Étape 1 : utilisez le fractionnement binaire récursif pour développer un grand arbre sur les données d’entraînement.

Tout d’abord, nous utilisons un algorithme glouton appelé fractionnement binaire récursif pour développer un arbre de régression en utilisant la méthode suivante :

• Considérez toutes les variables prédictives X ₁ , X ₂ , … , X _p et toutes les valeurs possibles des points de coupure pour chacun des prédicteurs, puis choisissez le prédicteur et le point de coupure de telle sorte que l’arbre résultant ait le RSS (erreur type résiduelle) le plus bas. .
  • Pour les arbres de classification, nous choisissons le prédicteur et le point de coupure de telle sorte que l’arbre résultant ait le taux d’erreurs de classification le plus bas.
• Répétez ce processus, en vous arrêtant uniquement lorsque chaque nœud terminal a moins d’un certain nombre minimum d’observations.

Cet algorithme est gourmand car à chaque étape du processus de construction de l’arbre, il détermine la meilleure répartition à effectuer en fonction uniquement de cette étape, plutôt que de regarder vers l’avenir et de choisir une répartition qui conduira à un meilleur arbre global dans une étape future.

Étape 2 : Appliquer l’élagage de complexité de coût au grand arbre pour obtenir une séquence des meilleurs arbres, en fonction de α.

Une fois que nous avons fait pousser le grand arbre, nous devons ensuite l’ élaguer en utilisant une méthode connue sous le nom d’élagage complexe, qui fonctionne comme suit :

• Pour chaque arbre possible avec T nœuds terminaux, trouvez l’arbre qui minimise RSS + α|T|.
• Notez que lorsque nous augmentons la valeur de α, les arbres avec plus de nœuds terminaux sont pénalisés. Cela garantit que l’arborescence ne devient pas trop complexe.

Ce processus aboutit à une séquence des meilleurs arbres pour chaque valeur de α.

Étape 3 : Utilisez la validation croisée k fois pour choisir α.

Une fois que nous avons trouvé le meilleur arbre pour chaque valeur de α, nous pouvons appliquer une validation croisée k fois pour choisir la valeur de α qui minimise l’erreur de test.

Étape 4 : Choisissez le modèle final.

Enfin, nous choisissons le modèle final comme celui qui correspond à la valeur de α choisie.

Avantages et inconvénients des modèles CART

Les modèles CART offrent les avantages suivants :

• Ils sont faciles à interpréter.
• Ils sont faciles à expliquer.
• Ils sont faciles à visualiser.
• Ils peuvent être appliqués à la fois aux problèmes de régression et de classification .

Cependant, les modèles CART présentent les inconvénients suivants :

• Ils ont tendance à ne pas avoir autant de précision prédictive que les autres algorithmes d’apprentissage automatique non linéaires. Cependant, en regroupant de nombreux arbres de décision avec des méthodes telles que le bagging, le boosting et les forêts aléatoires, leur précision prédictive peut être améliorée.

Connexe : Comment ajuster les arbres de classification et de régression dans R