Comment ajuster les arbres de classification et de régression dans R

Lorsque la relation entre un ensemble de variables prédictives et une variable de réponse est linéaire, des méthodes telles que la régression linéaire multiple peuvent produire des modèles prédictifs précis.

Toutefois, lorsque la relation entre un ensemble de prédicteurs et une réponse est plus complexe, les méthodes non linéaires peuvent souvent produire des modèles plus précis.

L’une de ces méthodes est celle des arbres de classification et de régression (CART), qui utilisent un ensemble de variables prédictives pour créer des arbres de décision qui prédisent la valeur d’une variable de réponse.

Si la variable de réponse est continue, nous pouvons construire des arbres de régression et si la variable de réponse est catégorielle, nous pouvons construire des arbres de classification.

Ce didacticiel explique comment créer des arbres de régression et de classification dans R.

Exemple 1 : Construire un arbre de régression dans R

Pour cet exemple, nous utiliserons l’ensemble de données Hitters du package ISLR , qui contient diverses informations sur 263 joueurs de baseball professionnels.

Nous utiliserons cet ensemble de données pour construire un arbre de régression qui utilise les variables prédictives des circuits et des années jouées pour prédire le salaire d’un joueur donné.

Utilisez les étapes suivantes pour créer cet arbre de régression.

Étape 1 : Chargez les packages nécessaires.

Tout d’abord, nous allons charger les packages nécessaires pour cet exemple :

library(ISLR) #contains Hitters dataset
library(rpart) #for fitting decision trees
library(rpart.plot) #for plotting decision trees

Étape 2 : Construisez l’arbre de régression initial.

Tout d’abord, nous allons construire un grand arbre de régression initial. Nous pouvons garantir que l’arbre est grand en utilisant une petite valeur pour cp , qui signifie « paramètre de complexité ».

Cela signifie que nous effectuerons de nouvelles divisions sur l’arbre de régression tant que le R-carré global du modèle augmente d’au moins la valeur spécifiée par cp.

Nous utiliserons ensuite la fonction printcp() pour imprimer les résultats du modèle :

#build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart.control(cp=.0001))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error  xerror    xstd
1  0.24674996      0   1.00000 1.00756 0.13890
2  0.10806932      1   0.75325 0.76438 0.12828
3  0.01865610      2   0.64518 0.70295 0.12769
4  0.01761100      3   0.62652 0.70339 0.12337
5  0.01747617      4   0.60891 0.70339 0.12337
6  0.01038188      5   0.59144 0.66629 0.11817
7  0.01038065      6   0.58106 0.65697 0.11687
8  0.00731045      8   0.56029 0.67177 0.11913
9  0.00714883      9   0.55298 0.67881 0.11960
10 0.00708618     10   0.54583 0.68034 0.11988
11 0.00516285     12   0.53166 0.68427 0.11997
12 0.00445345     13   0.52650 0.68994 0.11996
13 0.00406069     14   0.52205 0.68988 0.11940
14 0.00264728     15   0.51799 0.68874 0.11916
15 0.00196586     16   0.51534 0.68638 0.12043
16 0.00016686     17   0.51337 0.67577 0.11635
17 0.00010000     18   0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Étape 3 : Taillez l’arbre.

Ensuite, nous allons élaguer l’arbre de régression pour trouver la valeur optimale à utiliser pour cp (le paramètre de complexité) qui conduit à l’erreur de test la plus faible.

Notez que la valeur optimale pour cp est celle qui conduit à l’ erreur x la plus faible dans la sortie précédente, qui représente l’erreur sur les observations à partir des données de validation croisée.

#identify best cp value to use
best <- tree$cptable[which.min(tree$cptable[,"xerror"]),"CP"]

#produce a pruned tree based on the best cp value
pruned_tree <- prune(tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen=0, #use full names for factor labels
    extra=1, #display number of obs. for each terminal node
    roundint=F, #don't round to integers in output
    digits=5) #display 5 decimal places in output

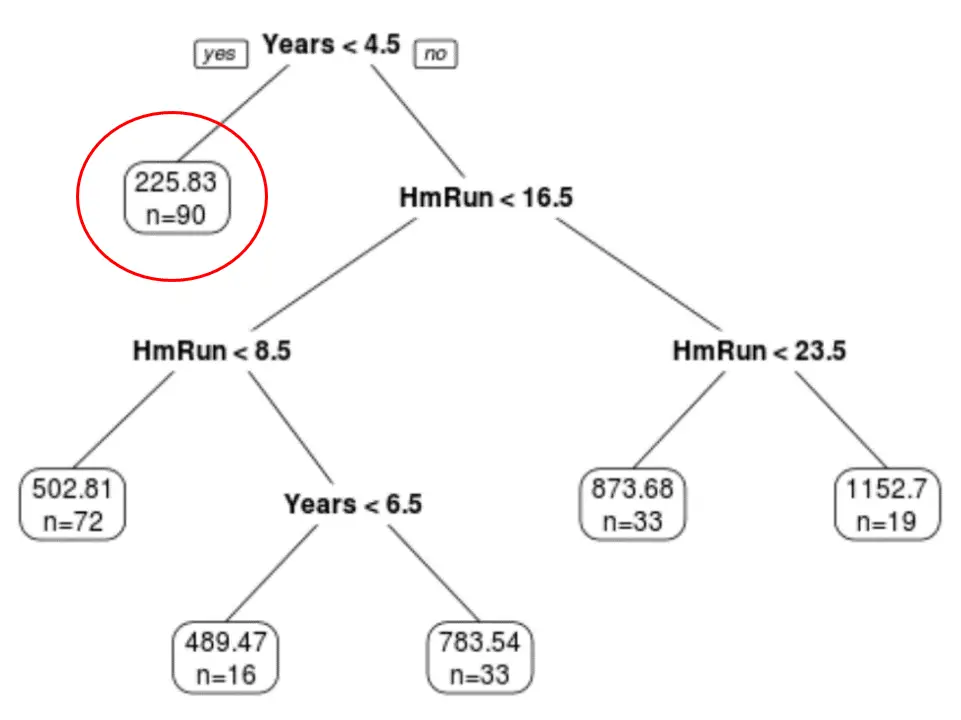
Nous pouvons voir que l’arbre élagué final comporte six nœuds terminaux. Chaque nœud terminal affiche le salaire prévu des joueurs dans ce nœud ainsi que le nombre d’observations de l’ensemble de données d’origine qui appartiennent à cette note.

Par exemple, nous pouvons voir que dans l’ensemble de données d’origine, il y avait 90 joueurs avec moins de 4,5 ans d’expérience et que leur salaire moyen était de 225,83 000 $.

Étape 4 : Utilisez l’arbre pour faire des prédictions.

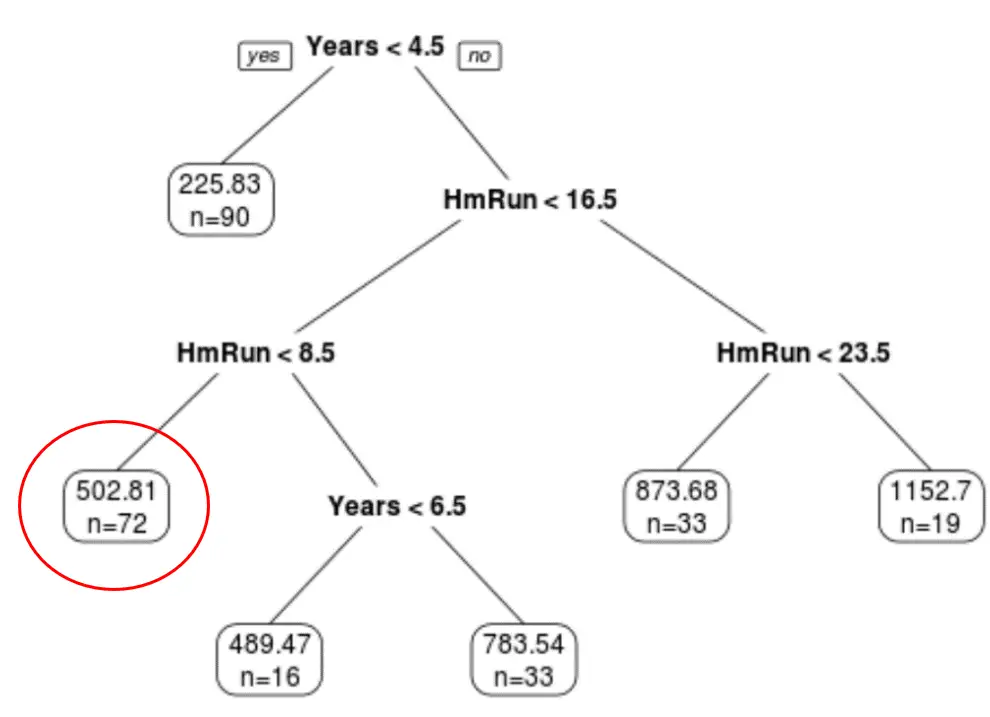
Nous pouvons utiliser l’arbre élagué final pour prédire le salaire d’un joueur donné en fonction de ses années d’expérience et de ses circuits moyens.

Par exemple, un joueur qui a 7 ans d’expérience et 4 circuits en moyenne a un salaire prévu de 502,81 000 $ .

Nous pouvons utiliser la fonction prédire() dans R pour confirmer ceci :

#define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079 

Exemple 2 : Construire un arbre de classification dans R

Pour cet exemple, nous utiliserons l’ensemble de données ptitanic du package rpart.plot , qui contient diverses informations sur les passagers à bord du Titanic.

Nous utiliserons cet ensemble de données pour créer un arbre de classification qui utilise les variables prédictives class , sex et age pour prédire si un passager donné a survécu ou non.

Utilisez les étapes suivantes pour créer cet arbre de classification.

Étape 1 : Chargez les packages nécessaires.

Tout d’abord, nous allons charger les packages nécessaires pour cet exemple :

library(rpart) #for fitting decision trees
library(rpart.plot) #for plotting decision trees

Étape 2 : Construisez l’arbre de classification initial.

Tout d’abord, nous allons construire un grand arbre de classification initial. Nous pouvons garantir que l’arbre est grand en utilisant une petite valeur pour cp , qui signifie « paramètre de complexité ».

Cela signifie que nous effectuerons de nouvelles divisions sur l’arbre de classification tant que l’ajustement global du modèle augmente d’au moins la valeur spécifiée par cp.

Nous utiliserons ensuite la fonction printcp() pour imprimer les résultats du modèle :

#build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart.control(cp=.0001))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age    pclass sex   

Root node error: 500/1309 = 0.38197

n= 1309 

      CP nsplit rel error xerror     xstd
1 0.4240      0     1.000  1.000 0.035158
2 0.0140      1     0.576  0.576 0.029976
3 0.0095      3     0.548  0.578 0.030013
4 0.0070      7     0.510  0.552 0.029517
5 0.0050      9     0.496  0.528 0.029035
6 0.0025     11     0.486  0.532 0.029117
7 0.0020     19     0.464  0.536 0.029198
8 0.0001     22     0.458  0.528 0.029035

Étape 3 : Taillez l’arbre.

Ensuite, nous allons élaguer l’arbre de régression pour trouver la valeur optimale à utiliser pour cp (le paramètre de complexité) qui conduit à l’erreur de test la plus faible.

Notez que la valeur optimale pour cp est celle qui conduit à l’ erreur x la plus faible dans la sortie précédente, qui représente l’erreur sur les observations à partir des données de validation croisée.

#identify best cp value to use
best <- tree$cptable[which.min(tree$cptable[,"xerror"]),"CP"]

#produce a pruned tree based on the best cp value
pruned_tree <- prune(tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen=0, #use full names for factor labels
    extra=1, #display number of obs. for each terminal node
    roundint=F, #don't round to integers in output
    digits=5) #display 5 decimal places in output

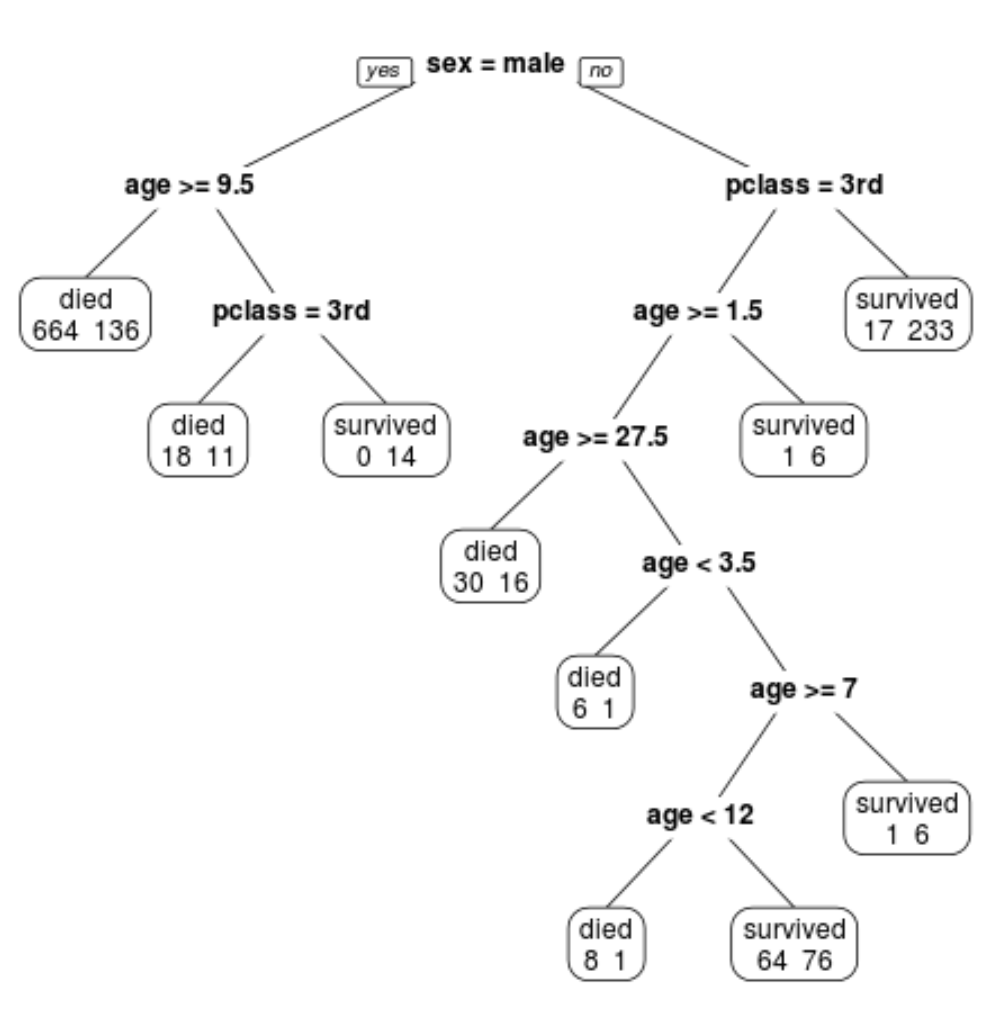
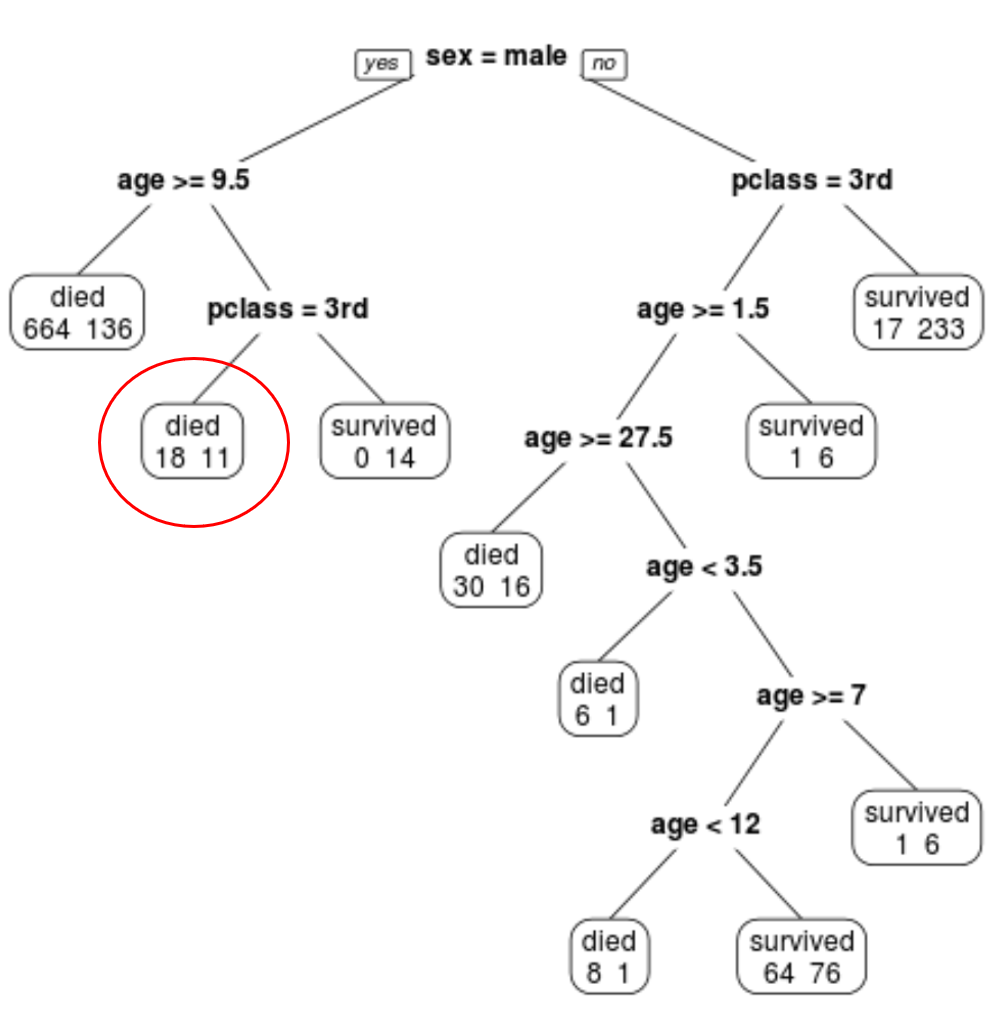
Nous pouvons voir que l’arbre élagué final comporte 10 nœuds terminaux. Chaque nœud terminal indique le nombre de passagers décédés ainsi que le nombre de survivants.

Par exemple, dans le nœud le plus à gauche, nous voyons que 664 passagers sont morts et 136 ont survécu.

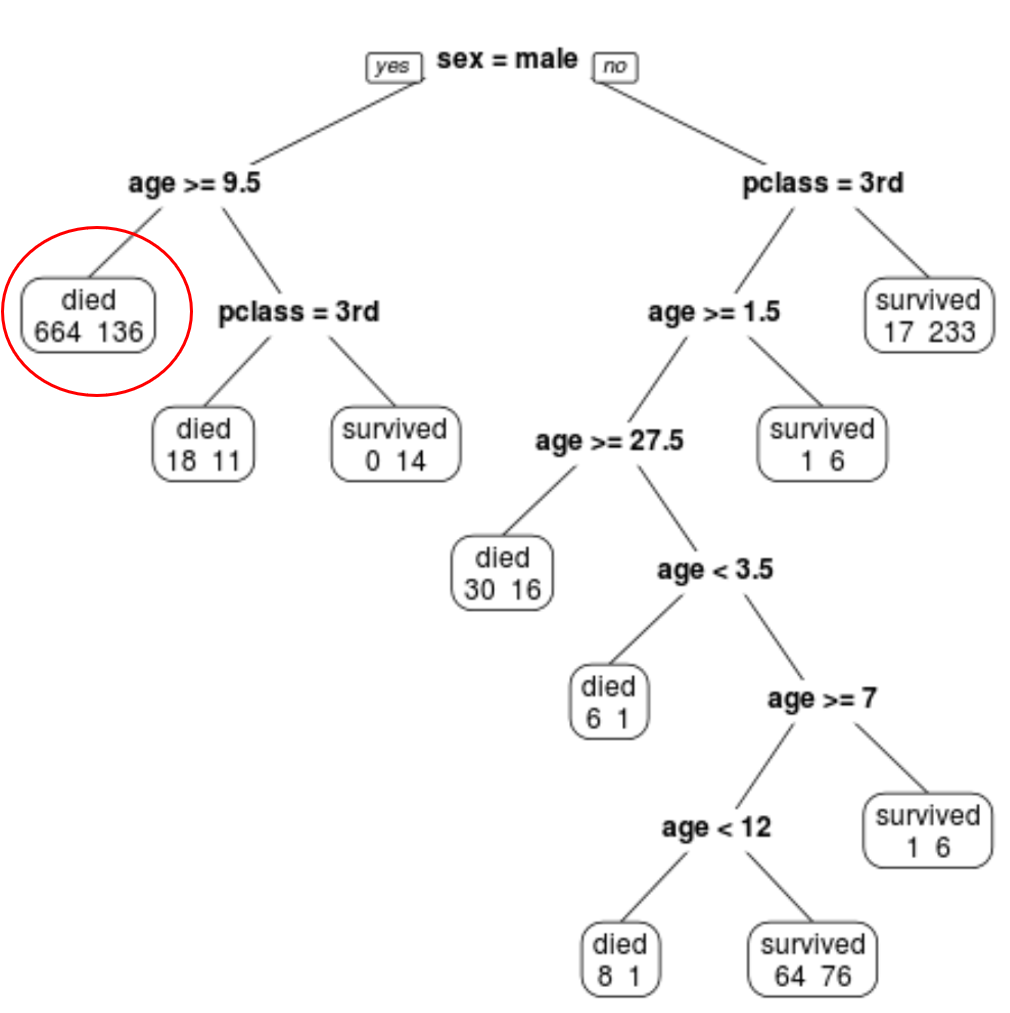
Étape 4 : Utilisez l’arbre pour faire des prédictions.

Nous pouvons utiliser l’arbre final élagué pour prédire la probabilité qu’un passager donné survive en fonction de sa classe, de son âge et de son sexe.

Par exemple, un passager de sexe masculin âgé de 8 ans et en 1re classe a une probabilité de survie de 11/29 = 37,9 %.

Vous pouvez trouver le code R complet utilisé dans ces exemples ici .