Comment calculer l’asymétrie & Aplatissement en R

En statistiques, l’asymétrie et l’aplatissement sont deux façons de mesurer la forme d’une distribution.

L’asymétrie est une mesure de l’asymétrie d’une distribution. Cette valeur peut être positive ou négative.

• Une asymétrie négative indique que la queue se trouve sur le côté gauche de la distribution, qui s’étend vers des valeurs plus négatives.
• Une asymétrie positive indique que la queue se trouve du côté droit de la distribution, qui s’étend vers des valeurs plus positives.
• Une valeur de zéro indique qu’il n’y a aucune asymétrie dans la distribution, ce qui signifie que la distribution est parfaitement symétrique.

L’aplatissement est une mesure permettant de savoir si une distribution est à queue lourde ou légère par rapport à unedistribution normale .

• L’aplatissement d’une distribution normale est de 3.
• Si une distribution donnée a un kurtosis inférieur à 3, elle est dite playkurtique , ce qui signifie qu’elle a tendance à produire moins de valeurs aberrantes et moins extrêmes que la distribution normale.
• Si une distribution donnée a un aplatissement supérieur à 3, elle est dite leptokurtique , ce qui signifie qu’elle a tendance à produire plus de valeurs aberrantes que la distribution normale.

Remarque : Certaines formules (définition de Fisher) soustraient 3 de l’aplatissement pour faciliter la comparaison avec la distribution normale. En utilisant cette définition, une distribution aurait un aplatissement supérieur à une distribution normale si elle avait une valeur d’aplatissement supérieure à 0.

Ce didacticiel explique comment calculer à la fois l’asymétrie et l’aplatissement d’un ensemble de données donné dans R.

Exemple : asymétrie et aplatissement dans R

Supposons que nous ayons l’ensemble de données suivant :

data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Nous pouvons visualiser rapidement la distribution des valeurs dans cet ensemble de données en créant un histogramme :

hist(data, col='steelblue')

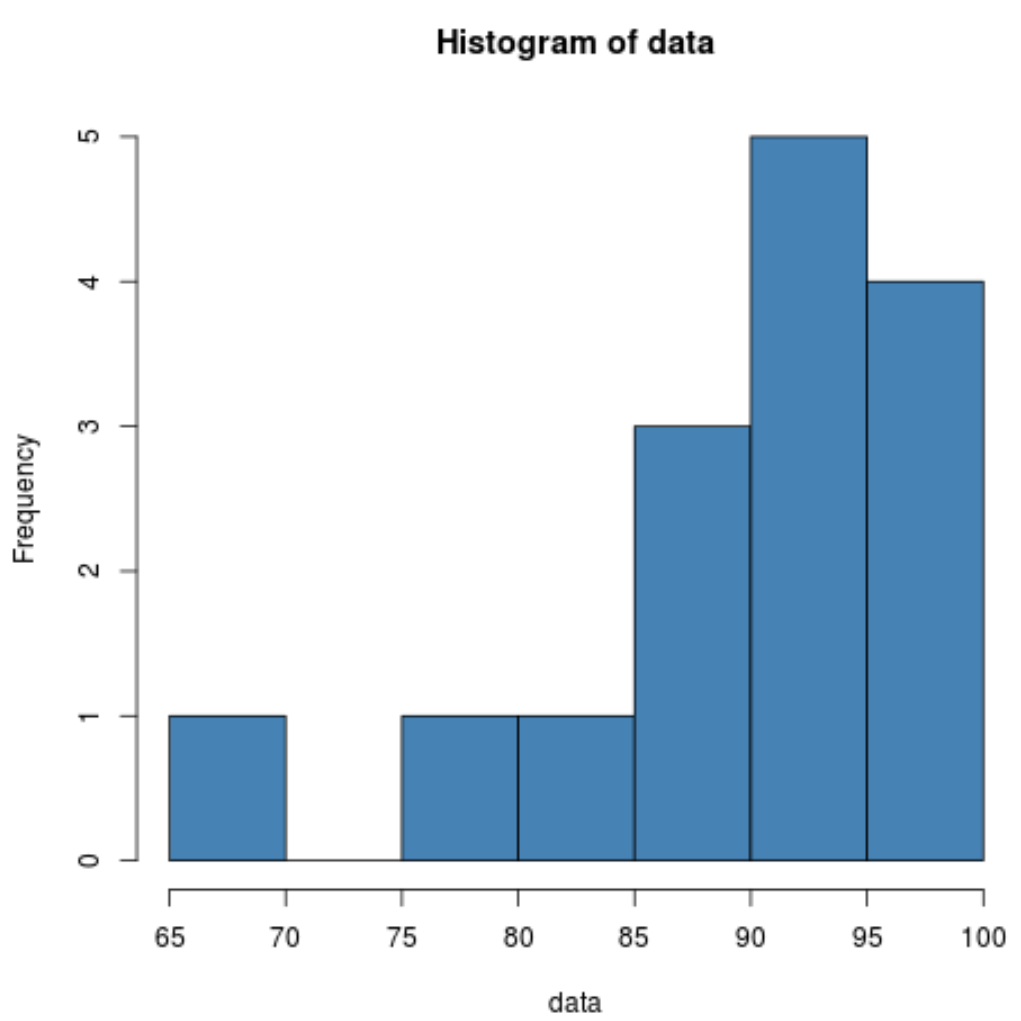
L’histogramme nous montre que la distribution semble être asymétrique à gauche. Autrement dit, une plus grande partie des valeurs sont concentrées sur le côté droit de la distribution.

Pour calculer l’asymétrie et l’aplatissement de cet ensemble de données, nous pouvons utiliser les fonctions skewness() et kurtosis() de la bibliothèque de moments dans R :

library(moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

L’asymétrie s’avère être de -1,391777 et l’aplatissement s’avère être de 4,177865 .

Puisque l’asymétrie est négative, cela indique que la distribution est asymétrique à gauche. Cela confirme ce que nous avons vu dans l’histogramme.

Puisque l’aplatissement est supérieur à 3, cela indique que la distribution a plus de valeurs dans les queues par rapport à une distribution normale.

La bibliothèque de moments propose également la fonction jarque.test() , qui effectue un test d’ajustement qui détermine si les exemples de données présentent ou non une asymétrie et un aplatissement correspondant à une distribution normale. Les hypothèses nulles et alternatives de ce test sont les suivantes :

Hypothèse nulle : l’ensemble de données a une asymétrie et un aplatissement qui correspondent à une distribution normale.

Hypothèse alternative : l’ensemble de données présente une asymétrie et un aplatissement qui ne correspondent pas à une distribution normale.

Le code suivant montre comment effectuer ce test :

jarque.test(data)

	Jarque-Bera Normality Test

data:  data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

La valeur p du test s’avère être de 0,05756 . Puisque cette valeur n’est pas inférieure à α = 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer que cet ensemble de données présente une asymétrie et un aplatissement différents de la distribution normale.

Vous pouvez trouver la documentation complète de la bibliothèque de moments ici .

Bonus : calculateur d’asymétrie et d’aplatissement

Vous pouvez également calculer l’asymétrie pour un ensemble de données donné à l’aide du calculateur d’asymétrie et d’aplatissement statistique , qui calcule automatiquement l’asymétrie et l’aplatissement pour un ensemble de données donné.