Comment calculer l’asymétrie & Aplatissement en SAS

En statistiques, l’asymétrie et l’aplatissement sont deux façons de mesurer la forme d’une distribution.

L’asymétrie mesure l’asymétrie d’une distribution.

• Une asymétrie négative indique que la queue se trouve du côté gauche de la distribution.
• Une asymétrie positive indique que la queue se trouve du côté droit de la distribution.
• Une valeur de zéro indique qu’il n’y a aucune asymétrie dans la distribution, ce qui signifie que la distribution est parfaitement symétrique.

L’aplatissement mesure si une distribution est à queue lourde ou légère par rapport à unedistribution normale .

• L’aplatissement d’une distribution normale est 0.
• Si une distribution donnée a un kurtosis inférieur à 0, elle est dite playkurtique , ce qui signifie qu’elle a tendance à produire moins de valeurs aberrantes et moins extrêmes que la distribution normale.
• Si une distribution donnée a un aplatissement supérieur à 0, elle est dite leptokurtique , ce qui signifie qu’elle a tendance à produire plus de valeurs aberrantes que la distribution normale.

Pour calculer l’asymétrie et l’aplatissement des variables dans SAS, vous pouvez utiliser les instructions SKEWNESS et KURTOSIS dans PROC MEANS .

L’exemple suivant montre comment utiliser ces instructions dans la pratique.

Exemple : calcul de l’asymétrie et de l’aplatissement dans SAS

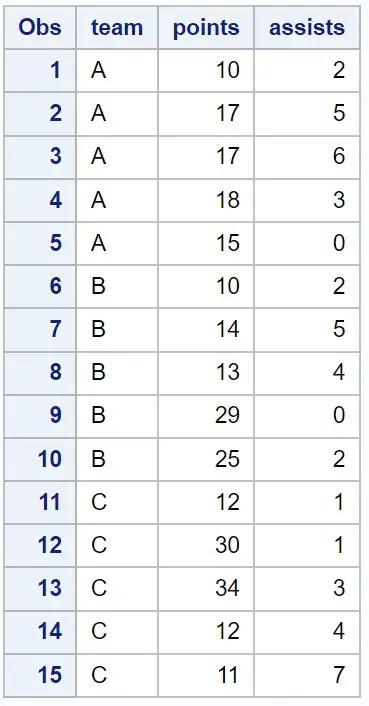
Supposons que nous ayons l’ensemble de données suivant dans SAS qui contient des informations sur divers joueurs de basket-ball :

/*create dataset*/
data my_data;
    input team $ points assists;
    datalines;
A 10 2
A 17 5
A 17 6
A 18 3
A 15 0
B 10 2
B 14 5
B 13 4
B 29 0
B 25 2
C 12 1
C 30 1
C 34 3
C 12 4
C 11 7
;
run;

/*view dataset*/
proc print data=my_data;

Nous pouvons utiliser PROC MEANS avec les instructions SKEWNESS et KURTOSIS pour calculer l’asymétrie et l’aplatissement de chaque variable numérique de l’ensemble de données :

/*calculate skewness and kurtosis for each numeric variable*/
proc means data=my_data SKEWNESS KURTOSIS;
run;

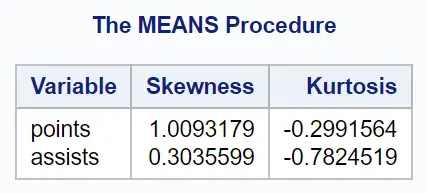
Le tableau en sortie affiche les valeurs d’asymétrie et d’aplatissement pour chaque variable numérique de l’ensemble de données :

(1) points

• La variable points a une asymétrie de 1,009 . Puisque cette valeur est supérieure à 0, cela signifie que la queue se trouve du côté droit de la distribution.
• La variable points a un kurtosis de -0,299 . Puisque cette valeur est inférieure à 0, cela signifie que la distribution comporte un peu moins de valeurs aberrantes et moins extrêmes que la distribution normale.

(2) aide

• La variable des passes décisives a une asymétrie de 0,304 . Puisque cette valeur est supérieure à 0, cela signifie que la queue se trouve du côté droit de la distribution.
• La variable d’assistance a un kurtosis de -0,782 . Puisque cette valeur est inférieure à 0, cela signifie que la distribution comporte moins de valeurs aberrantes et moins extrêmes que la distribution normale.

Pour visualiser la distribution des valeurs pour chaque variable numérique de l’ensemble de données, vous pouvez utiliser PROC UNIVARIATE pour créer des histogrammes pour les variables de points et d’assistance :

/*create histograms for points and assists variables*/
proc univariate data=my_data;
    var points assists;
    histogram points assists;
run;

Cela produit l’histogramme suivant pour la variable points :

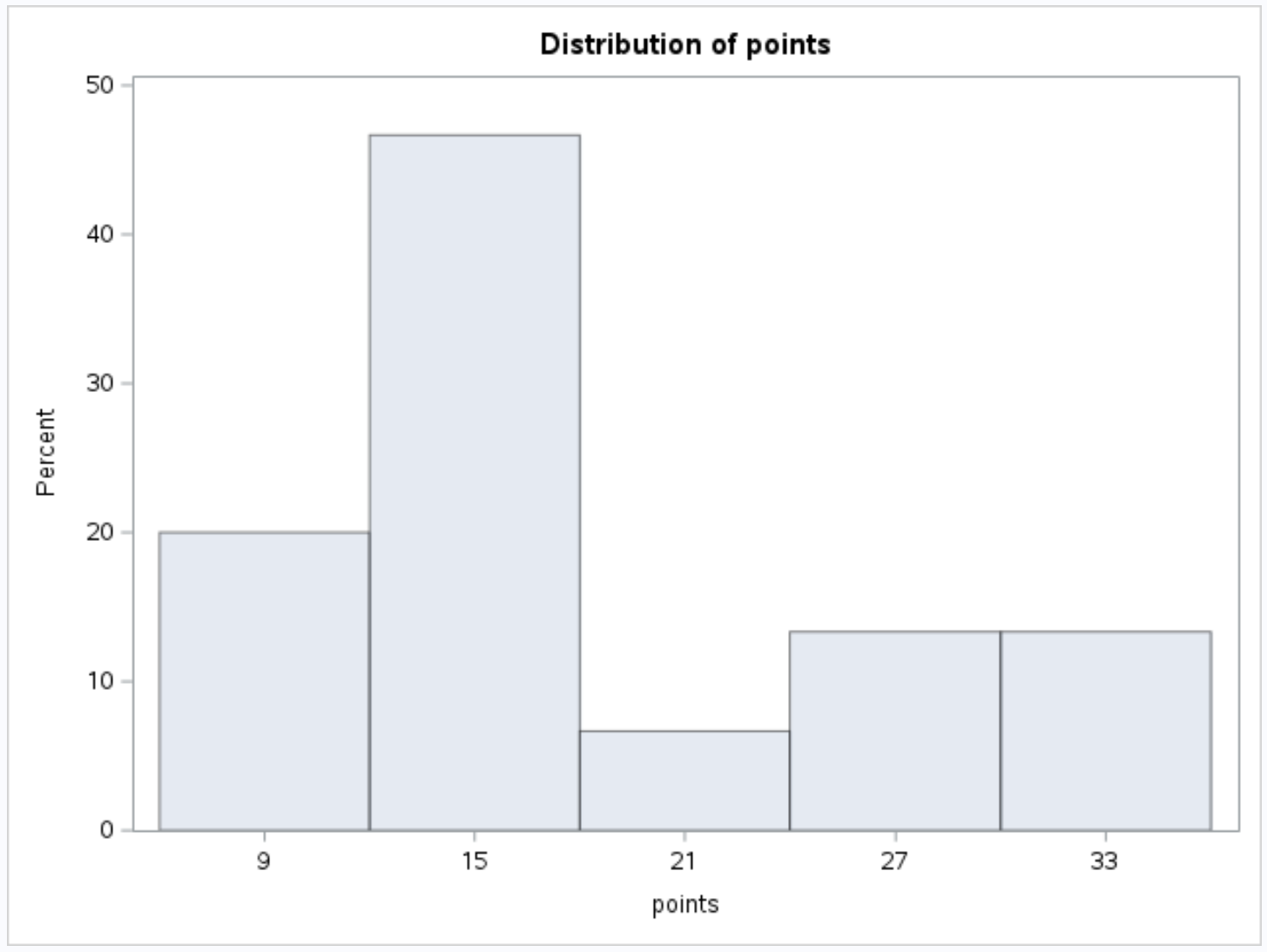
Et l’histogramme suivant pour la variable d’assistance :

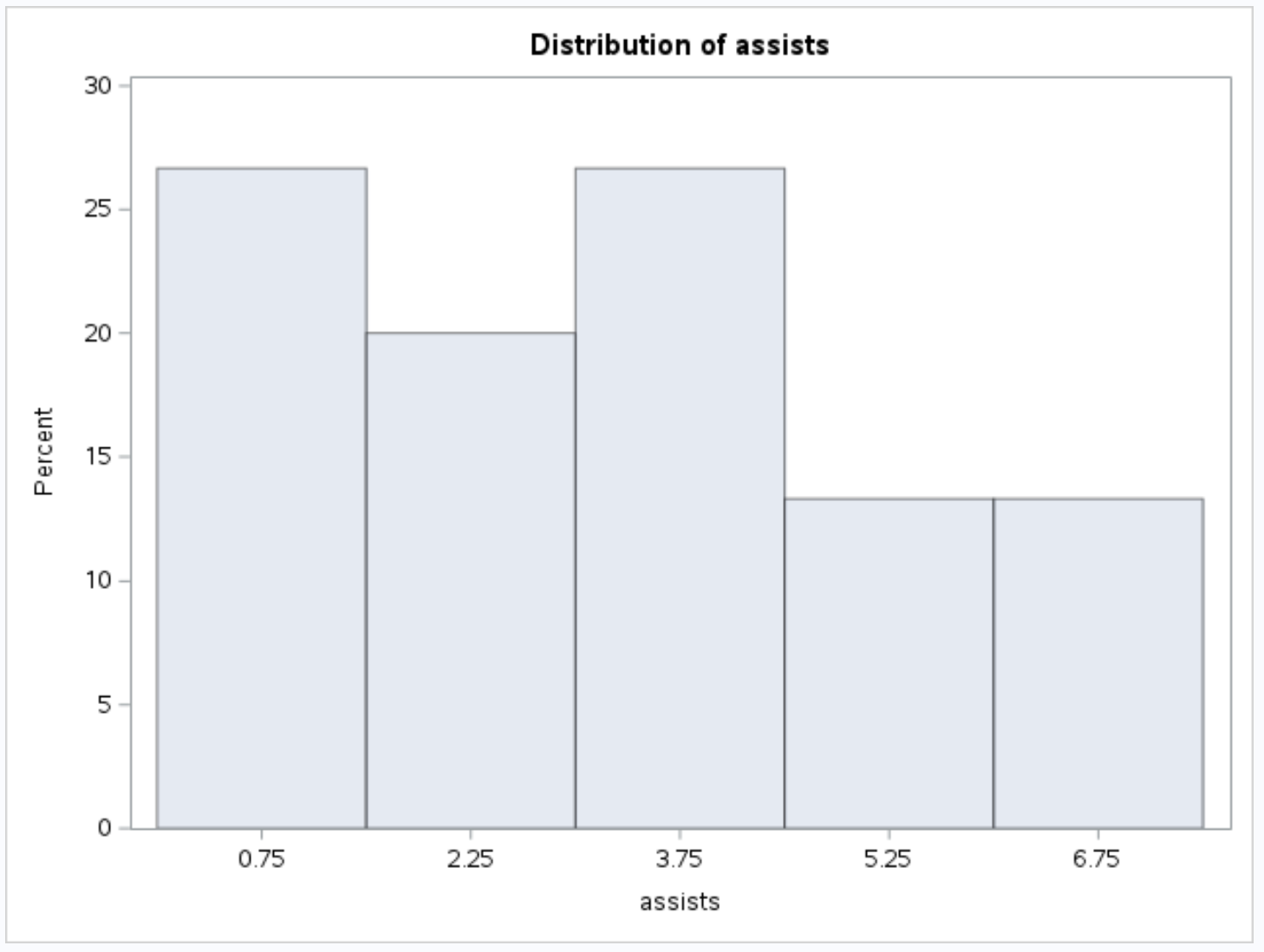
Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment calculer des statistiques descriptives dans SAS
Comment créer des tableaux de fréquences dans SAS
Comment calculer les centiles dans SAS
Comment créer des tableaux croisés dynamiques dans SAS