Un guide de la procédure Benjamini-Hochberg
Chaque fois que vous effectuez un test statistique, il est possible que vous obteniez une valeur p inférieure à 0,05 par pur hasard, même si votre hypothèse nulle est vraie.
Par exemple, supposons que vous vouliez savoir si une certaine plante a une hauteur moyenne supérieure à 10 pouces. Vos hypothèses nulles et alternatives pour le test seraient :
H 0 : μ = 10 pouces
H A : μ > 10 pouces
Pour tester cette hypothèse, vous pouvez sortir et collecter un échantillon aléatoire de 20 plantes à mesurer. Même si la véritable hauteur moyenne de cette espèce de plante est de 10 pouces, il est possible que vous ayez sélectionné un échantillon de 20 plantes inhabituellement hautes, ce qui vous amènera à rejeter l’hypothèse nulle.
Même si l’hypothèse nulle était vraie (la hauteur moyenne de cette plante était en réalité de 10 pouces), vous l’avez rejetée. En statistiques, nous appelons cela une « fausse découverte ». Vous prétendez avoir fait une découverte – un « résultat significatif » – mais c’est en réalité faux.
Imaginez maintenant que vous effectuiez 100 tests statistiques à la fois. En utilisant un niveau alpha de 0,05, il n’y a que 5 % de chances de faire une fausse découverte avec un test individuel, mais comme vous effectuez un si grand nombre de tests, vous vous attendez à ce qu’environ 5 sur 100 conduisent à de fausses découvertes.
Dans le monde moderne, les fausses découvertes peuvent constituer un problème courant puisque la technologie a permis aux chercheurs d’effectuer des centaines, voire des milliers de tests statistiques à la fois.
Par exemple, les chercheurs en médecine peuvent effectuer des tests statistiques sur des dizaines de milliers de gènes à la fois. Même avec un taux de fausses découvertes de seulement 5 %, cela signifie que des centaines de tests pourraient aboutir à de fausses découvertes.
Une façon de contrôler le taux de fausses découvertes consiste à utiliser ce qu’on appelle la procédure Benjamini-Hochberg.
La procédure Benjamini-Hochberg
La procédure Benjamini-Hochberg fonctionne comme suit :
Étape 1 : effectuez tous vos tests statistiques et trouvez la valeur p pour chaque test.
Étape 2 : Classez les valeurs p par ordre décroissant, en attribuant un rang à chacune d’entre elles : la plus petite valeur p a un rang de 1, la suivante la plus petite a un rang de 2, etc.
Étape 3 : Calculez la valeur critique de Benjamini-Hochberg pour chaque valeur p, en utilisant la formule (i/m)*Q
où:
i = rang de la valeur p
m = nombre total de tests
Q = votre taux de fausse découverte choisi
Étape 4 : Trouvez la plus grande valeur p inférieure à la valeur critique. Désignez chaque valeur p inférieure à cette valeur p comme étant significative.
L’exemple suivant illustre comment mener cette procédure avec des valeurs concrètes.
Exemple
Supposons que les chercheurs souhaitent déterminer si 20 variables différentes sont liées ou non aux maladies cardiaques. Ils effectuent 20 tests statistiques individuels à la fois et reçoivent une valeur p pour chaque test. Le tableau suivant montre les valeurs p pour chaque test, classées par ordre décroissant.
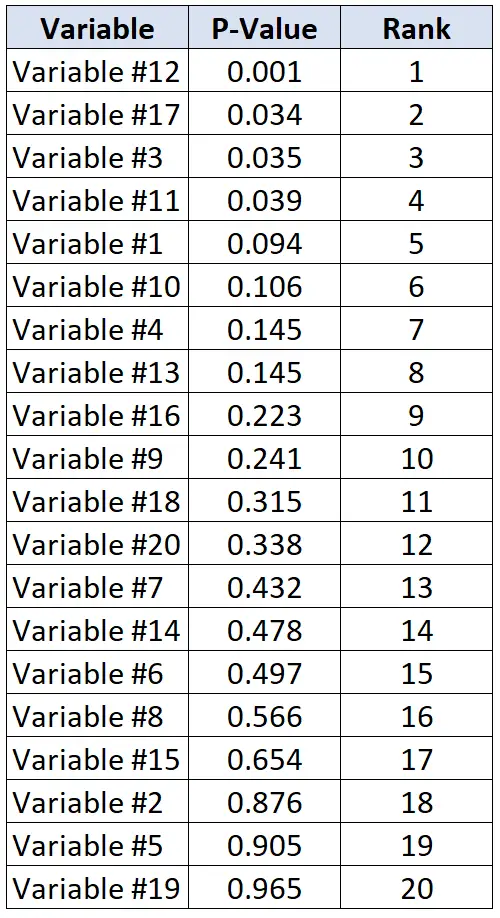
Supposons que les chercheurs soient prêts à accepter un taux de fausses découvertes de 20 %. Ainsi, pour calculer la valeur critique de Benjamini-Hochberg pour chaque valeur p, nous pouvons utiliser la formule suivante : (i/20)*0,2 où i = rang de la valeur p.
Le tableau suivant montre la valeur critique de Benjamini-Hochberg pour chaque valeur p individuelle :
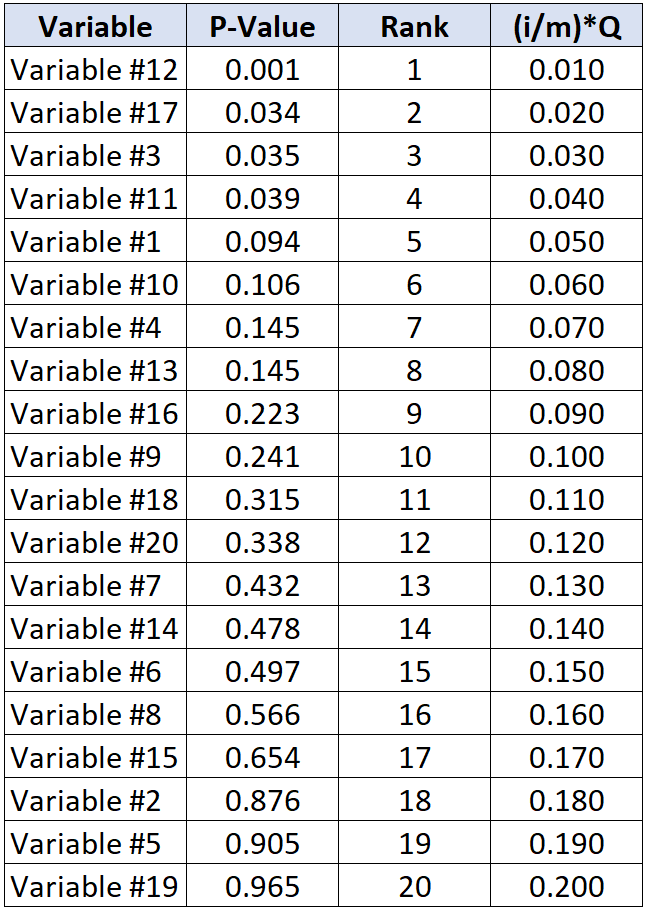
Le test avec la plus grande valeur p inférieure à sa valeur critique de Benjamini-Hochberg est la variable n° 11, qui a une valeur p de 0,039 et une valeur critique BH de 0,040.
Ainsi, ce test et tous les tests avec une valeur p plus petite seront considérés comme significatifs.
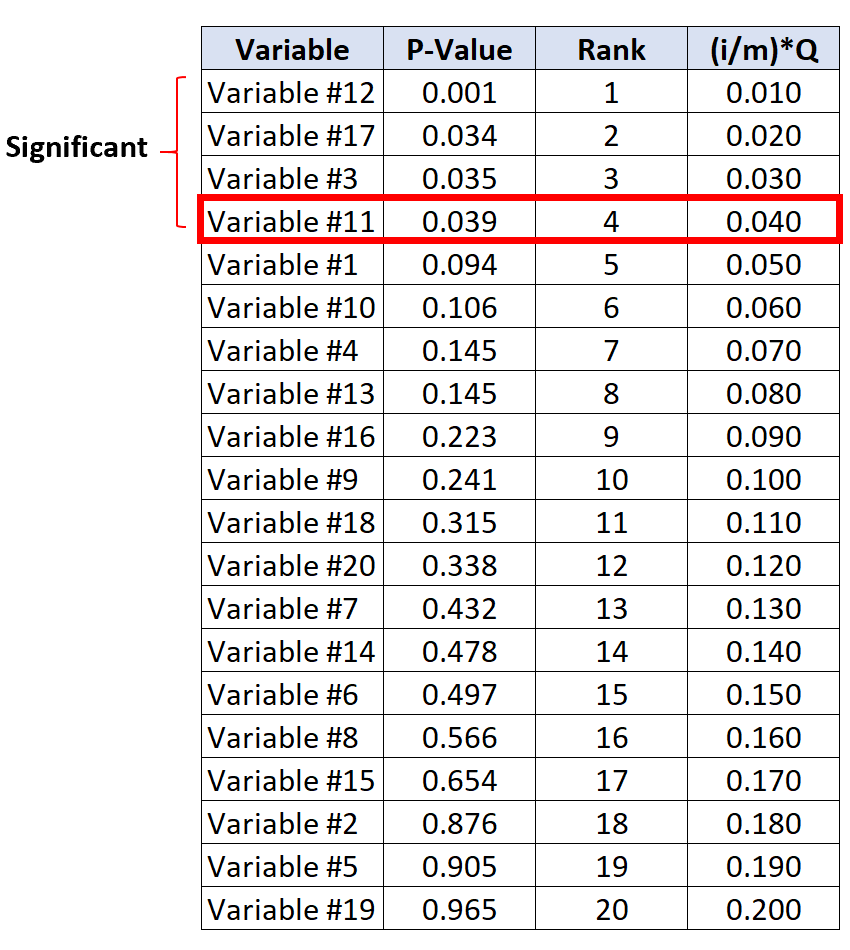
Notez que même si les variables n° 17 et n° 3 n’avaient pas de valeurs p inférieures à leurs valeurs critiques BH, elles sont toujours considérées comme significatives car elles ont des valeurs p plus petites que la variable n° 11.
Comment choisir un taux de fausse découverte
L’une des étapes les plus importantes de la procédure Benjamini-Hochberg consiste à choisir un taux de fausse découverte. Vous devez choisir votre taux de fausse découverte avant de collecter des données ou d’effectuer des tests statistiques.
En règle générale, vous effectuerez un grand nombre de tests statistiques au cours de la phase exploratoire de votre analyse, que vous suivrez ensuite avec d’autres tests pour approfondir vos résultats.
Si les tests de suivi sont peu coûteux, vous pouvez alors envisager de fixer un taux de fausses découvertes plus élevé, car même si vous avez quelques fausses découvertes, vous découvrirez probablement ces fausses découvertes lors de tests ultérieurs.
De plus, si le coût de manquer une découverte importante est élevé, vous souhaiterez peut-être augmenter votre taux de fausses découvertes afin de ne rien manquer d’important.
En fonction des coûts de vos recherches et de l’importance de ne manquer aucune découverte importante, le taux de fausses découvertes variera d’une situation à l’autre.
Ressources additionnelles
Une explication des valeurs P et de la signification statistique
Quel est le taux d’erreur par famille ?
