Quel est le compromis biais-variance dans l’apprentissage automatique ?

Pour évaluer les performances d’un modèle sur un ensemble de données, nous devons mesurer dans quelle mesure les prédictions du modèle correspondent aux données observées.

Pour les modèles de régression , la métrique la plus couramment utilisée est l’erreur quadratique moyenne (MSE), qui est calculée comme suit :

MSE = (1/n)*Σ(y _je – f(x _je )) ²

où:

• n : nombre total d’observations
• y _i : La valeur de réponse de la ^ième observation
• f(x _i ) : La valeur de réponse prédite de la i ^ème observation

Plus les prédictions du modèle sont proches des observations, plus la MSE sera faible.

Cependant, nous ne nous soucions que du test MSE – le MSE lorsque notre modèle est appliqué à des données invisibles. En effet, nous ne nous soucions que de la manière dont le modèle fonctionnera sur des données invisibles, et non sur des données existantes.

Par exemple, c’est bien si un modèle qui prédit les cours boursiers a un faible MSE sur les données historiques, mais nous voulons vraiment pouvoir utiliser le modèle pour prévoir avec précision les données futures.

Il s’avère que le test MSE peut toujours être décomposé en deux parties :

(1) La variance : fait référence à la quantité dont notre fonction f changerait si nous l’estimions en utilisant un ensemble d’entraînement différent.

(2) Le biais : fait référence à l’erreur introduite en approchant un problème réel, qui peut être extrêmement compliqué, par un modèle beaucoup plus simple.

Écrit en termes mathématiques :

Test MSE = Var( f̂( x ₀ )) + [Biais( f̂( x ₀ ))] ² + Var(ε)

Test MSE = Variance + Biais ² + Erreur irréductible

Le troisième terme, l’erreur irréductible, est l’erreur qui ne peut être réduite par aucun modèle simplement parce qu’il existe toujours du bruit dans la relation entre l’ensemble des variables explicatives et la variable de réponse .

Les modèles qui ont un biais élevé ont tendance à avoir une faible variance . Par exemple, les modèles de régression linéaire ont tendance à avoir un biais élevé (en supposant une relation linéaire simple entre les variables explicatives et la variable de réponse) et une faible variance (les estimations du modèle ne changeront pas beaucoup d’un échantillon à l’autre).

Cependant, les modèles ayant un faible biais ont tendance à avoir une variance élevée . Par exemple, les modèles non linéaires complexes ont tendance à avoir un faible biais (ne suppose pas une certaine relation entre les variables explicatives et la variable de réponse) avec une variance élevée (les estimations du modèle peuvent changer considérablement d’un échantillon d’apprentissage à l’autre).

Le compromis biais-variance

Le compromis biais-variance fait référence au compromis qui a lieu lorsque nous choisissons de réduire le biais, ce qui augmente généralement la variance, ou de réduire la variance, ce qui augmente généralement le biais.

Le graphique suivant offre un moyen de visualiser ce compromis :

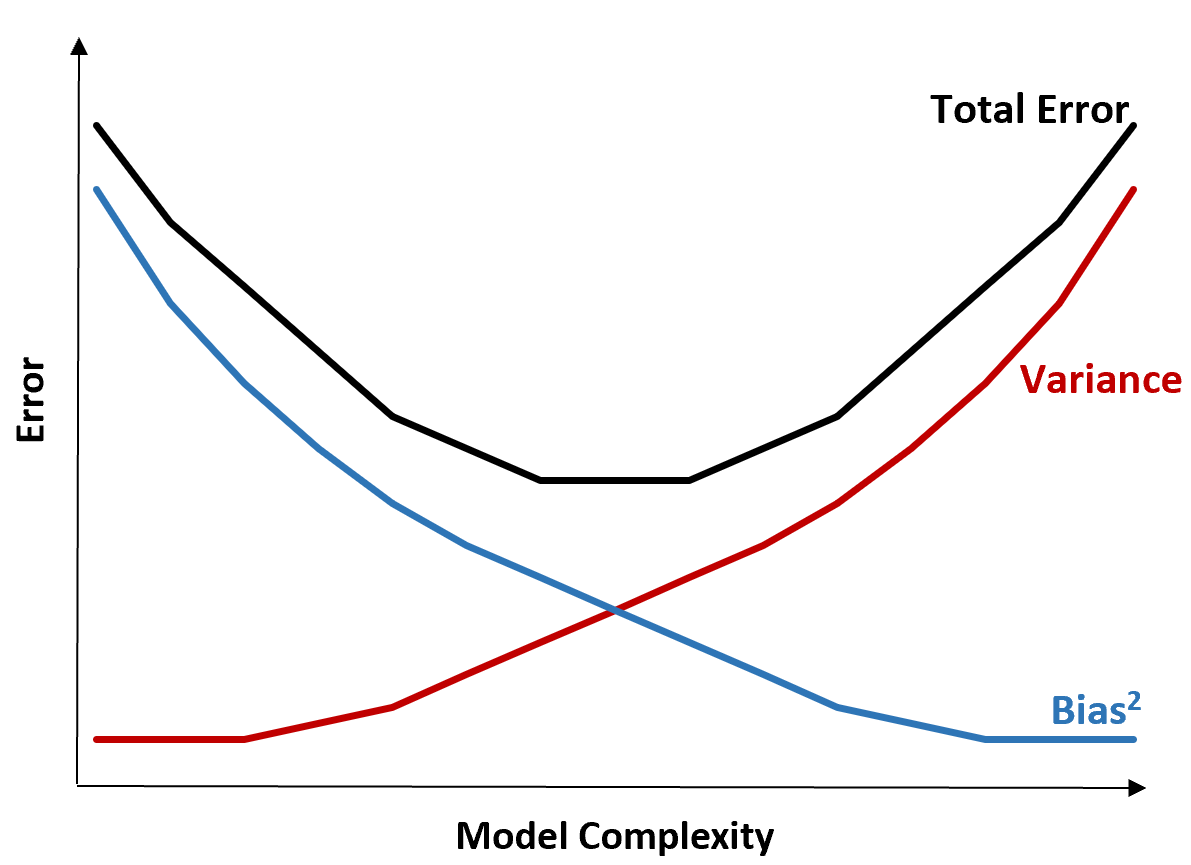
L’erreur totale diminue à mesure que la complexité d’un modèle augmente, mais seulement jusqu’à un certain point. Au-delà d’un certain point, la variance commence à augmenter et l’erreur totale commence également à augmenter.

En pratique, nous nous soucions uniquement de minimiser l’erreur totale d’un modèle, pas nécessairement de minimiser la variance ou le biais. Il s’avère que la manière de minimiser l’erreur totale consiste à trouver le bon équilibre entre variance et biais.

En d’autres termes, nous voulons un modèle suffisamment complexe pour capturer la véritable relation entre les variables explicatives et la variable de réponse, mais pas trop complexe pour détecter des modèles qui n’existent pas réellement.

Lorsqu’un modèle est trop complexe, il surajuste les données. Cela se produit parce qu’il est trop difficile de trouver des modèles dans les données d’entraînement qui sont simplement provoqués par le hasard. Ce type de modèle est susceptible d’être peu performant sur des données invisibles.

Mais lorsqu’un modèle est trop simple, il sous-estime les données. Cela se produit parce que l’on suppose que la véritable relation entre les variables explicatives et la variable de réponse est plus simple qu’elle ne l’est en réalité.

La manière de sélectionner des modèles optimaux dans l’apprentissage automatique consiste à trouver un équilibre entre biais et variance afin de minimiser l’erreur de test du modèle sur de futures données invisibles.

Dans la pratique, le moyen le plus courant de minimiser le MSE des tests est d’utiliser la validation croisée .