Binôme négatif vs Poisson : comment choisir un modèle de régression

La régression binomiale négative et la régression de Poisson sont deux types de modèles de régression qu’il convient d’utiliser lorsque la variable de réponse est représentée par des résultats de comptage discrets.

Voici quelques exemples de variables de réponse qui représentent des résultats de comptage discret :

• Le nombre d’étudiants diplômés d’un certain programme
• Le nombre d’accidents de la route à une certaine intersection
• Le nombre de participants qui terminent un marathon
• Le nombre de retours au cours d’un mois donné dans un magasin de détail

Si la variance est à peu près égale à la moyenne, alors un modèle de régression de Poisson s’adapte généralement bien à un ensemble de données.

Cependant, si la variance est significativement supérieure à la moyenne, un modèle de régression binomiale négative est généralement capable de mieux ajuster les données.

Il existe deux techniques que nous pouvons utiliser pour déterminer si la régression de Poisson ou la régression binomiale négative est plus appropriée pour un ensemble de données donné :

1. Parcelles résiduelles

Nous pouvons créer un tracé des résidus standardisés par rapport aux valeurs prédites à partir d’un modèle de régression.

Si la majorité des résidus standardisés se situent entre -2 et 2, un modèle de régression de Poisson est probablement approprié.

Cependant, si de nombreux résidus se situent en dehors de cette plage, un modèle de régression binomiale négative fournira probablement un meilleur ajustement.

2. Test du rapport de vraisemblance

Nous pouvons adapter un modèle de régression de Poisson et un modèle de régression binomiale négative au même ensemble de données, puis effectuer un test de rapport de vraisemblance.

Si la valeur p du test est inférieure à un certain niveau de signification (par exemple 0,05), nous pouvons alors conclure que le modèle de régression binomiale négative offre un ajustement nettement meilleur.

L’exemple suivant montre comment utiliser ces deux techniques dans R pour déterminer s’il est préférable d’utiliser un modèle de régression de Poisson ou de régression binomiale négative pour un ensemble de données donné.

Exemple : régression binomiale négative vs régression de Poisson

Supposons que nous voulions savoir combien de bourses d’études un joueur de baseball d’un lycée d’un comté donné reçoit en fonction de sa division scolaire (« A », « B » ou « C ») et de sa note à l’examen d’entrée à l’université (mesurée de 0 à 100). ).

Utilisez les étapes suivantes pour déterminer si un modèle de régression binomiale négative ou un modèle de régression de Poisson offre un meilleur ajustement aux données.

Étape 1 : Créer les données

Le code suivant crée l’ensemble de données avec lequel nous allons travailler, qui comprend des données sur 1 000 joueurs de baseball :

#make this example reproducible
set.seed(1)

#create dataset
data <- data.frame(offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c('A', 'B', 'C'), 100, replace = TRUE),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division     exam
1      0        A 66.22635
2      0        C 66.85974
3      0        A 77.87136
4      0        B 77.24617
5      0        A 62.31193
6      0        C 61.06622

Étape 2 : Ajuster un modèle de régression de Poisson et un modèle de régression binomiale négative

Le code suivant montre comment ajuster à la fois un modèle de régression de Poisson et un modèle de régression binomiale négative aux données :

#fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = 'poisson', data = data)

#fit negative binomial regression model
library(MASS)

nb_model <- glm.nb(offers ~ division + exam, data = data)

Étape 3 : Créer des tracés résiduels

Le code suivant montre comment produire des tracés résiduels pour les deux modèles.

#Residual plot for Poisson regression
p_res <- resid(p_model)
plot(fitted(p_model), p_res, col='steelblue', pch=16,
     xlab='Predicted Offers', ylab='Standardized Residuals', main='Poisson')
abline(0,0)

#Residual plot for negative binomial regression 
nb_res <- resid(nb_model)
plot(fitted(nb_model), nb_res, col='steelblue', pch=16,
     xlab='Predicted Offers', ylab='Standardized Residuals', main='Negative Binomial')
abline(0,0)

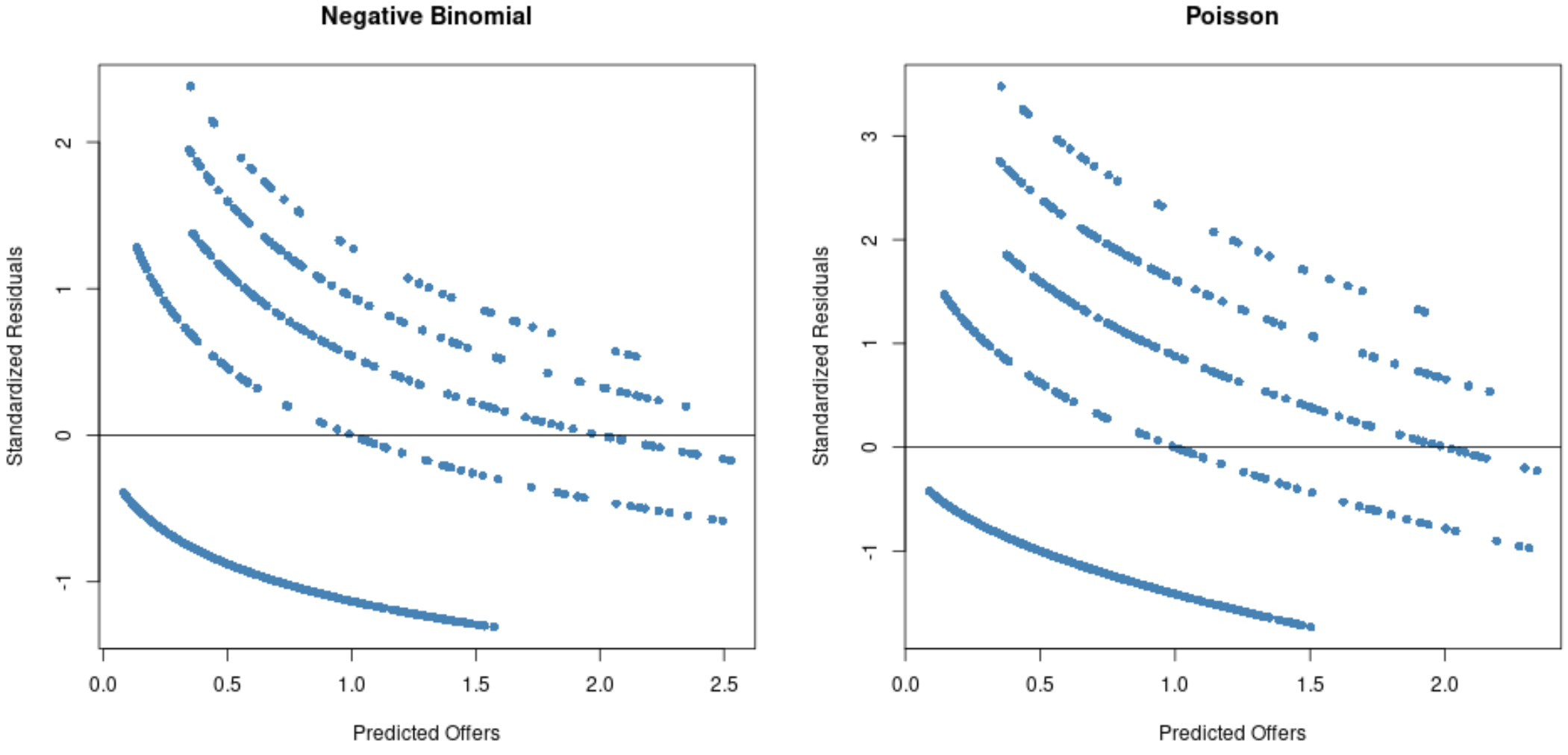
À partir des graphiques, nous pouvons voir que les résidus sont plus étalés pour le modèle de régression de Poisson (notez que certains résidus s’étendent au-delà de 3) par rapport au modèle de régression binomiale négative.

C’est le signe qu’un modèle de régression binomiale négative est probablement plus approprié puisque les résidus de ce modèle sont plus petits.

Étape 4 : Effectuer un test de rapport de vraisemblance

Enfin, nous pouvons effectuer un test du rapport de vraisemblance pour déterminer s’il existe une différence statistiquement significative dans l’ajustement des deux modèles de régression :

pchisq(2 * (logLik(nb_model) - logLik(p_model)), df = 1, lower.tail = FALSE)

'log Lik.' 3.508072e-29 (df=5)

La valeur p du test s’avère être 3,508072e-29 , ce qui est nettement inférieur à 0,05.

Ainsi, nous conclurions que le modèle de régression binomiale négative offre un ajustement significativement meilleur aux données par rapport au modèle de régression de Poisson.

Ressources additionnelles

Une introduction à la distribution binomiale négative
Une introduction à la distribution de Poisson