BinomPDF vs BinomCDF : la différence (plus des exemples)
La distribution binomiale est l’une des distributions les plus couramment utilisées dans toutes les statistiques.
Sur une calculatrice TI-84, vous pouvez utiliser deux fonctions pour trouver des probabilités liées à la distribution binomiale :
- binompdf(n, p, x) : recherche la probabilité qu’exactement x succès se produisent au cours de n essais où la probabilité de succès sur un essai donné est égale à p .
- binomcdf(n, p, x) : recherche la probabilité que x succès ou moins se produisent au cours de n essais où la probabilité de succès sur un essai donné est égale à p .
Vous pouvez accéder à chacune de ces fonctions sur une calculatrice TI-84 en appuyant sur 2nd puis en appuyant sur VARS . Cela vous amènera à un écran DISTR où vous pourrez ensuite utiliser binompdf() et binomcdf() :
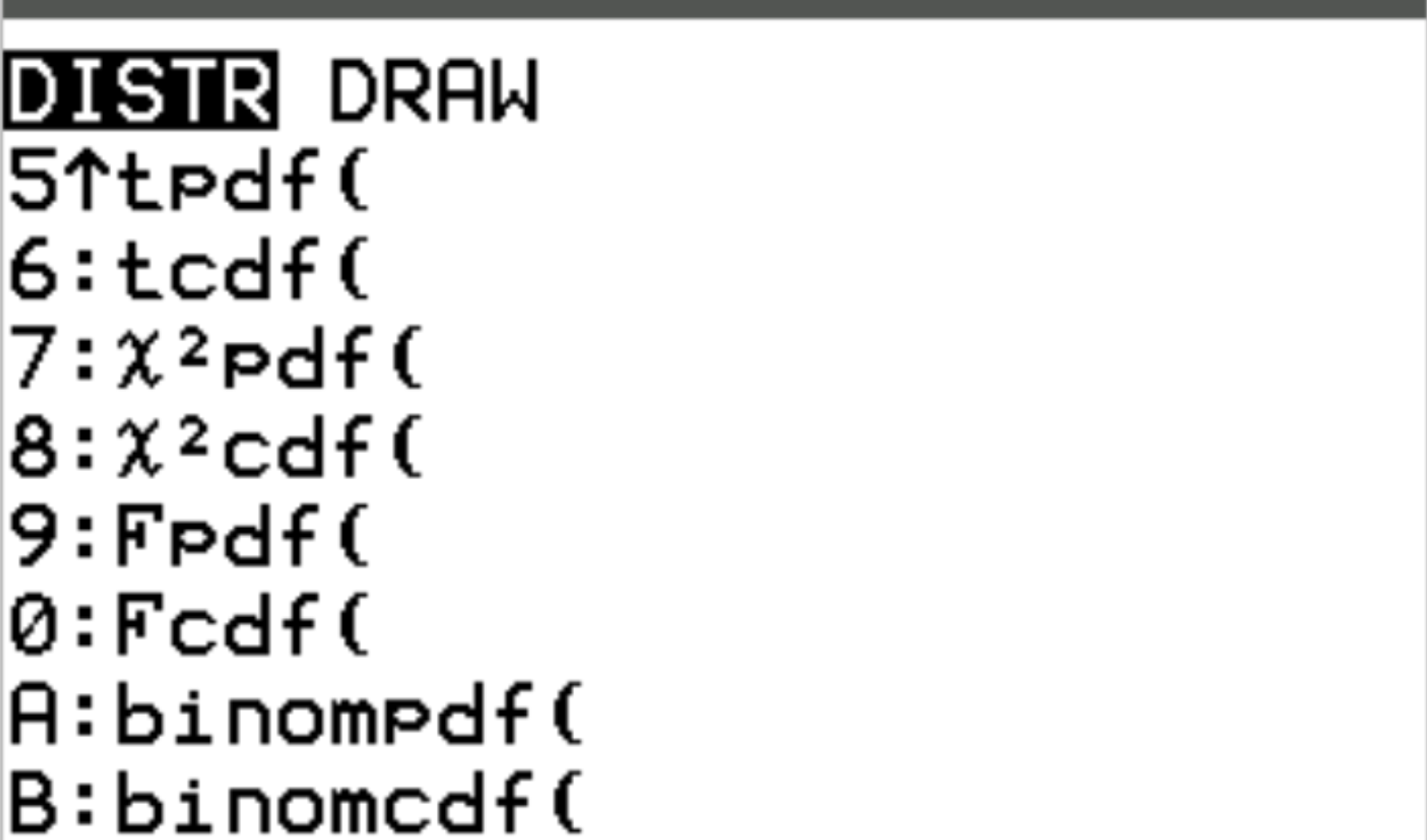
Les exemples suivants montrent comment utiliser chacune de ces fonctions dans la pratique.
Exemples : Comment utiliser Binompdf()
Les exemples suivants montrent comment utiliser la fonction binompdf() .
Exemple 1 : tentatives de lancer franc
Jessica réussit 80 % de ses tentatives de lancer franc. Si elle réussit 10 lancers francs, quelle est la probabilité qu’elle en réussisse exactement 7 ?
Pour répondre à cette question, nous pouvons taper la formule suivante :
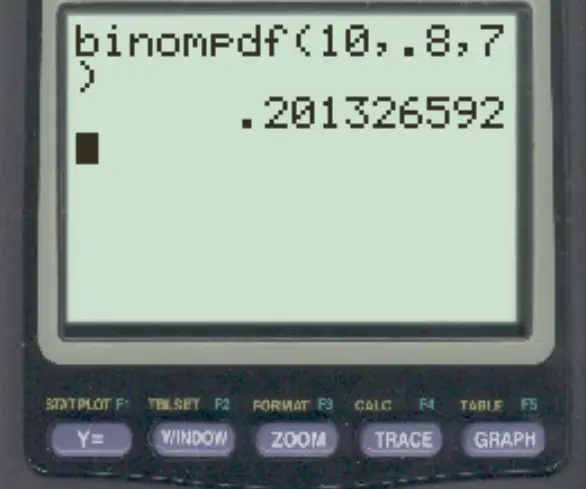
La probabilité qu’elle obtienne exactement 7 est de 0,2013 .
Exemple 2 : Transactions frauduleuses
Une banque sait que 3 % de toutes les transactions sont frauduleuses. Si 20 transactions ont lieu au cours d’une journée donnée, quelle est la probabilité qu’exactement 2 soient frauduleuses ?
Pour répondre à cette question, nous pouvons taper la formule suivante :
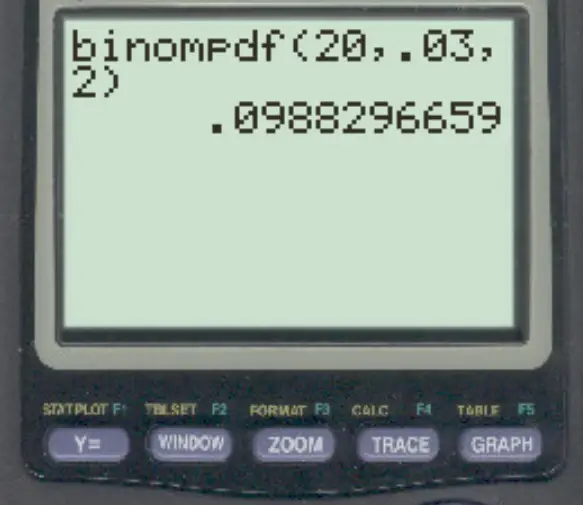
La probabilité qu’exactement 2 transactions soient frauduleuses est de 0,0988 .
Exemples : comment utiliser Binomcdf()
Les exemples suivants montrent comment utiliser la fonction binomcdf() .
Exemple 1 : tentatives de lancer franc
Jessica réussit 50 % de ses tentatives de lancer franc. Si elle réussit 10 lancers francs, quelle est la probabilité qu’elle en réussisse 7 ou moins ?
Pour répondre à cette question, nous pouvons taper la formule suivante :
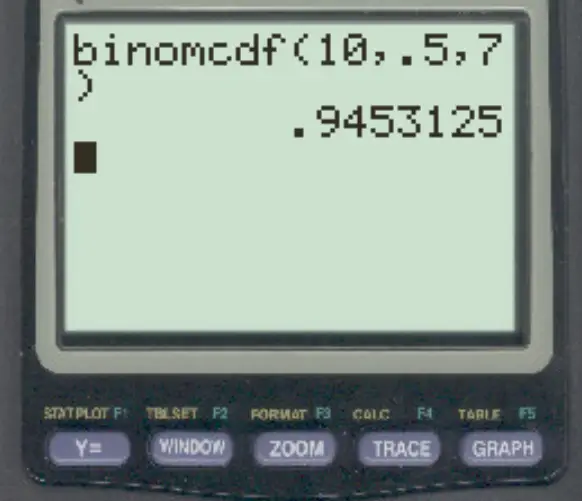
La probabilité qu’elle réalise 7 lancers francs ou moins est de 0,9453 .
Exemple 2 : Transactions frauduleuses
Une banque sait que 3 % de toutes les transactions sont frauduleuses. Si 20 transactions ont lieu dans une journée donnée, quelle est la probabilité que plus de 2 transactions soient frauduleuses ?
Pour répondre à cette question, nous pouvons taper la formule suivante :
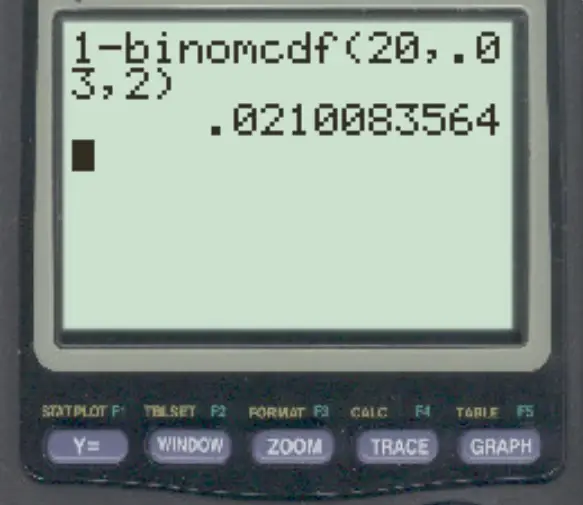
La probabilité que plus de 2 transactions soient frauduleuses est de 0,021 .
Ressources additionnelles
Calculateur de distribution binomiale
Comment effectuer un test binomial dans Excel
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus