Comment effectuer un bootstrapping dans R (avec des exemples)

Le bootstrapping est une méthode qui peut être utilisée pour estimer l’erreur type de n’importe quelle statistique et produire un intervalle de confiance pour la statistique.

Le processus de base pour le bootstrap est le suivant :

• Prenez k échantillons répétés avec remplacement à partir d’un ensemble de données donné.
• Pour chaque échantillon, calculez la statistique qui vous intéresse.
• Cela donne k estimations différentes pour une statistique donnée, que vous pouvez ensuite utiliser pour calculer l’erreur type de la statistique et créer un intervalle de confiance pour la statistique.

Nous pouvons effectuer un bootstrap dans R en utilisant les fonctions suivantes de la bibliothèque de démarrage :

1. Générez des échantillons bootstrap.

boot(données, statistiques, R, …)

où:

• data : un vecteur, une matrice ou un bloc de données
• statistique : une fonction qui produit la ou les statistiques à amorcer
• R : Nombre de répétitions bootstrap

2. Générez un intervalle de confiance bootstrap.

boot.ci (objet de démarrage, conf, type)

où:

• bootobject : Un objet renvoyé par la fonction boot()
• conf : L’intervalle de confiance à calculer. La valeur par défaut est 0,95
• type : Type d’intervalle de confiance à calculer. Les options incluent « norme », « basic », « stud », « perc », « bca » et « all » – La valeur par défaut est « all »

Les exemples suivants montrent comment utiliser ces fonctions dans la pratique.

Exemple 1 : amorcer une seule statistique

Le code suivant montre comment calculer l’erreur standard pour leR-carré d’un modèle de régression linéaire simple :

set.seed(0)
library(boot)

#define function to calculate R-squared
rsq_function <- function(formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return(summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    disp)


Bootstrap Statistics :
     original      bias    std. error
t1* 0.7183433 0.002164339  0.06513426

D’après les résultats, nous pouvons voir :

• Le R-carré estimé pour ce modèle de régression est de 0,7183433 .
• L’erreur type pour cette estimation est de 0,06513426 .

Nous pouvons également visualiser rapidement la distribution des échantillons bootstrapés :

plot(reps)

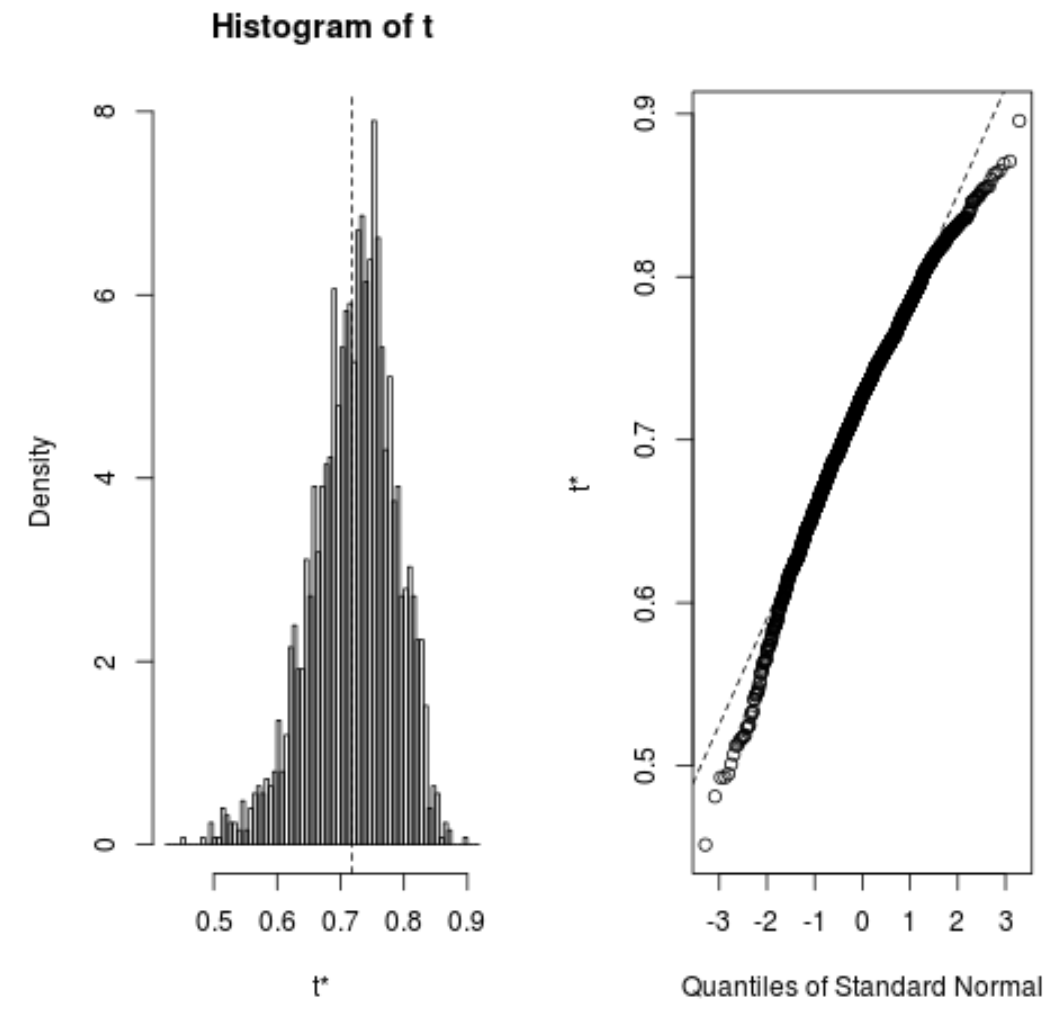
Nous pouvons également utiliser le code suivant pour calculer l’intervalle de confiance à 95 % pour le R-carré estimé du modèle :

#calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type="bca")

CALL : 
boot.ci(boot.out = reps, type = "bca")

Intervals : 
Level       BCa          
95%   ( 0.5350,  0.8188 )  
Calculations and Intervals on Original Scale

À partir du résultat, nous pouvons voir que l’intervalle de confiance bootstrapé à 95 % pour les vraies valeurs R au carré est de (0,5350, 0,8188).

Exemple 2 : amorcer plusieurs statistiques

Le code suivant montre comment calculer l’erreur type pour chaque coefficient dans un modèle de régression linéaire multiple :

set.seed(0)
library(boot)

#define function to calculate fitted regression coefficients
coef_function <- function(formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return(coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    disp)


Bootstrap Statistics :
       original        bias    std. error
t1* 29.59985476 -5.058601e-02  1.49354577
t2* -0.04121512  6.549384e-05  0.00527082

D’après les résultats, nous pouvons voir :

• Le coefficient estimé pour l’ordonnée à l’origine du modèle est 29,59985476 et l’erreur type de cette estimation est 1,49354577 .
• Le coefficient estimé pour la variable prédictive disp dans le modèle est de -0,04121512 et l’erreur type de cette estimation est de 0,00527082 .

Nous pouvons également visualiser rapidement la distribution des échantillons bootstrapés :

plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

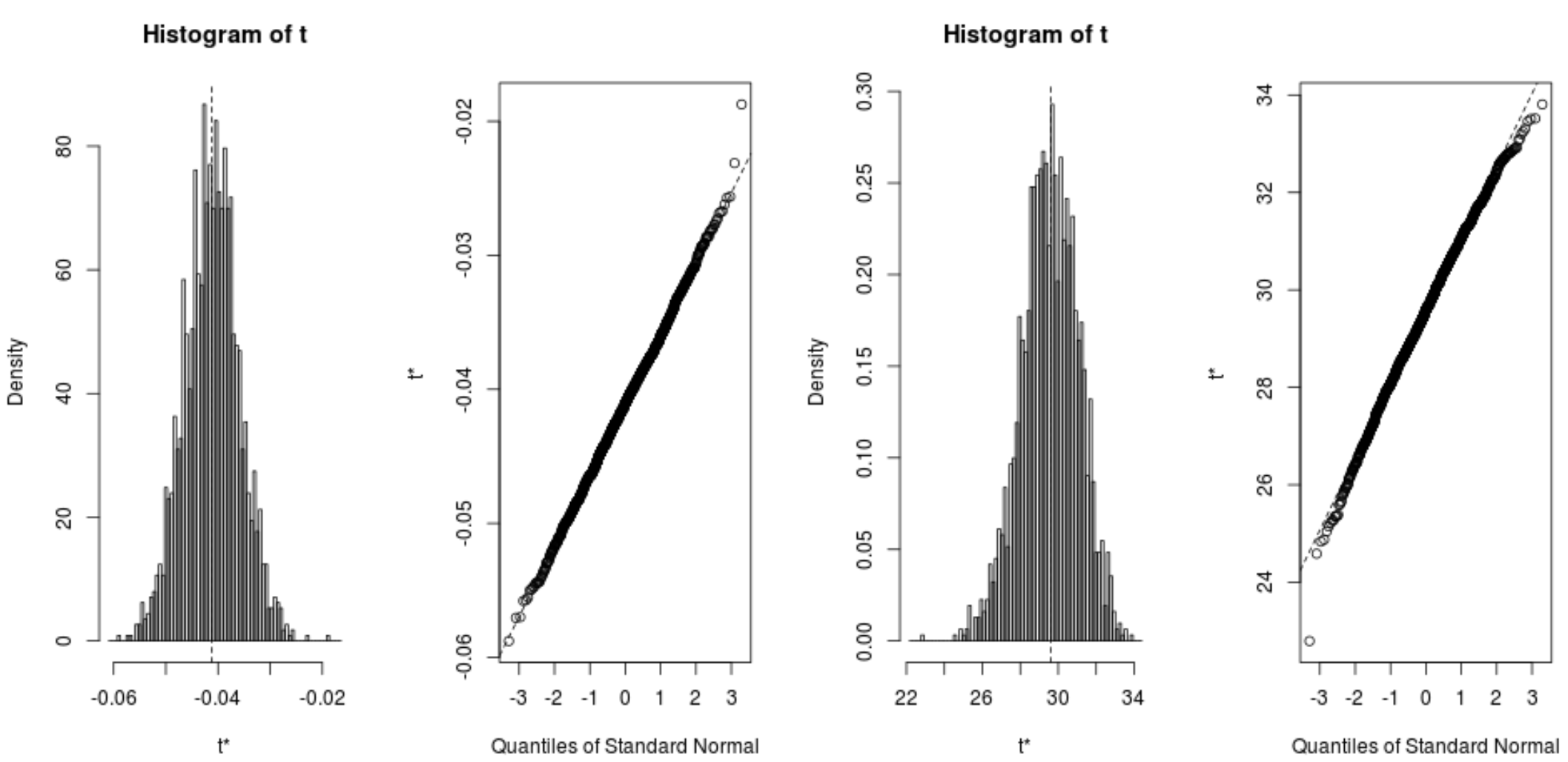
On peut également utiliser le code suivant pour calculer les intervalles de confiance à 95 % pour chaque coefficient :

#calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type="bca", index=1) #intercept of model
boot.ci(reps, type="bca", index=2) #disp predictor variable

CALL : 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals : 
Level       BCa          
95%   (26.78, 32.66 )  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL : 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals : 
Level       BCa          
95%   (-0.0520, -0.0312 )  
Calculations and Intervals on Original Scale

À partir des résultats, nous pouvons voir que les intervalles de confiance bootstrapés à 95 % pour les coefficients du modèle sont les suivants :

• CI pour l’interception : (26,78, 32,66)
• CI pour disp : (-.0520, -.0312)

Ressources additionnelles

Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Introduction aux intervalles de confiance