Diagramme en boîte et moustaches (boxplot)

Cet article explique ce qu’est un diagramme en boîte à moustaches, également connu sous le nom de diagramme en boîte (ou diagramme en boîte). Vous découvrirez comment ces types de diagrammes statistiques sont réalisés et un exercice résolu d’un diagramme en boîte et moustaches ainsi que son interprétation.

Qu’est-ce qu’un diagramme en boîte et moustaches ?

Le diagramme en boîte à moustaches , également appelé diagramme en boîte ou boxplot , est un graphique qui représente visuellement un ensemble de données statistiques à l’aide de quartiles.

La principale caractéristique du box and whisker plot est qu’il permet de visualiser rapidement la dispersion d’une série de données, puisqu’il indique les quartiles, la médiane, les valeurs extrêmes et les valeurs aberrantes des données.

Ainsi, ce type de diagramme est formé d’une boîte rectangulaire et de quelques lignes (ou moustaches) dont ressortent les valeurs suivantes :

• Les limites de la case indiquent les premier et troisième quartiles (Q ₁ et Q ₃ ). Et la ligne verticale à l’intérieur de la boîte est la médiane (équivalente au deuxième quartile Q ₂ ).
• Les limites des moustaches (ou bras) sont les valeurs extrêmes , c’est-à-dire la valeur minimale et la valeur maximale de la série de données.
• Les points en dehors des moustaches sont les valeurs atypiques ( outliers ), ou en d’autres termes, des données qui ont probablement été mal mesurées et ne doivent donc pas être prises en compte dans l’étude statistique.

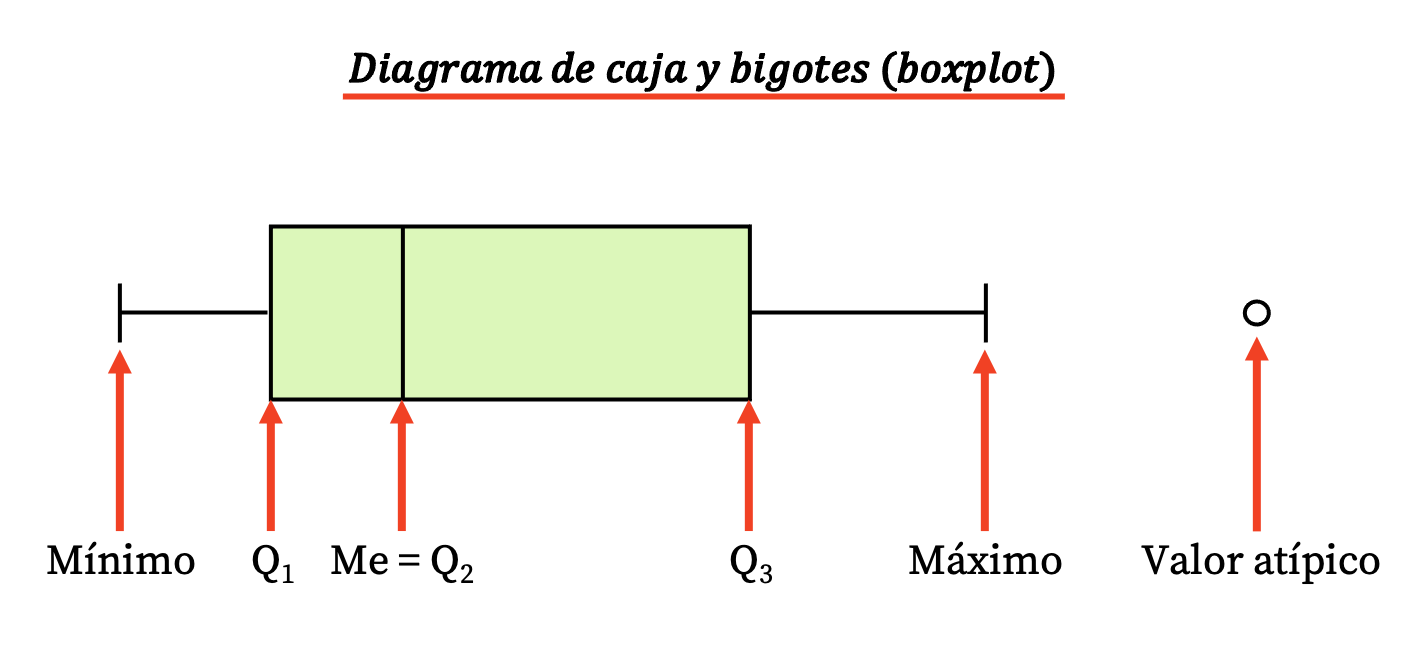
Notez que la différence entre le troisième et le premier quartile est l’intervalle interquartile (ou intervalle interquartile), une autre mesure de la dispersion statistique.

Les diagrammes en boîte et moustaches sont très utiles pour comparer des variables numériques. Cependant, il ne convient pas pour représenter des variables catégorielles.

Comment créer un tracé en boîte et en moustaches

Pour créer un box and whisker plot (ou boxplot) à partir d’une série de données, les étapes suivantes doivent être effectuées :

1. Triez les exemples de données statistiques.
2. Calculez les quartiles (Q ₁ , Q ₂ et Q ₃ ) et représentez-les comme la case du diagramme. Les premier et troisième quartiles correspondent aux limites de la case, et pour représenter la médiane (le deuxième quartile) il faut tracer une ligne à l’intérieur de la case où se trouve sa valeur.
3. Calculez l’intervalle interquartile, qui est égal au troisième quartile moins le premier quartile.



4. Calculez les valeurs admissibles LI et LS, dont les formules sont :





5. Identifiez les valeurs aberrantes de l’échantillon, qui sont les valeurs inférieures à LI ou supérieures à LS. Représentez ces valeurs en dehors de la portée des moustaches avec des points.
6. Identifiez et représentez les valeurs extrêmes, qui sont la plus petite valeur et la plus grande valeur dans l’intervalle formé par LI et LS. Ces valeurs représentent la fin des deux moustaches du diagramme.

Exemple de diagramme en boîte et moustaches

Compte tenu de la définition et de la théorie du box and whisker plot (ou boxplot), vous trouverez ci-dessous un exemple concret pour mieux comprendre le concept et voir comment ce type de tracé statistique est réalisé.

• Dessinez un diagramme en boîte à moustaches (ou boxplot) de l’ensemble de données statistiques suivant.

Dans ce cas, les données sont déjà classées du plus petit au plus grand, aucune modification n’est donc nécessaire. Sinon, nous devrions d’abord trier les exemples de données.

Dans un deuxième temps, nous extrayons les quartiles de l’échantillon :

Une fois que nous avons calculé les trois quartiles, nous trouvons l’écart interquartile en soustrayant le quartile 3 moins le quartile 1 :

On calcule maintenant les limites LI et LS, qui sont les valeurs à partir desquelles une donnée est considérée comme atypique. Pour ce faire, il faut utiliser les formules suivantes :

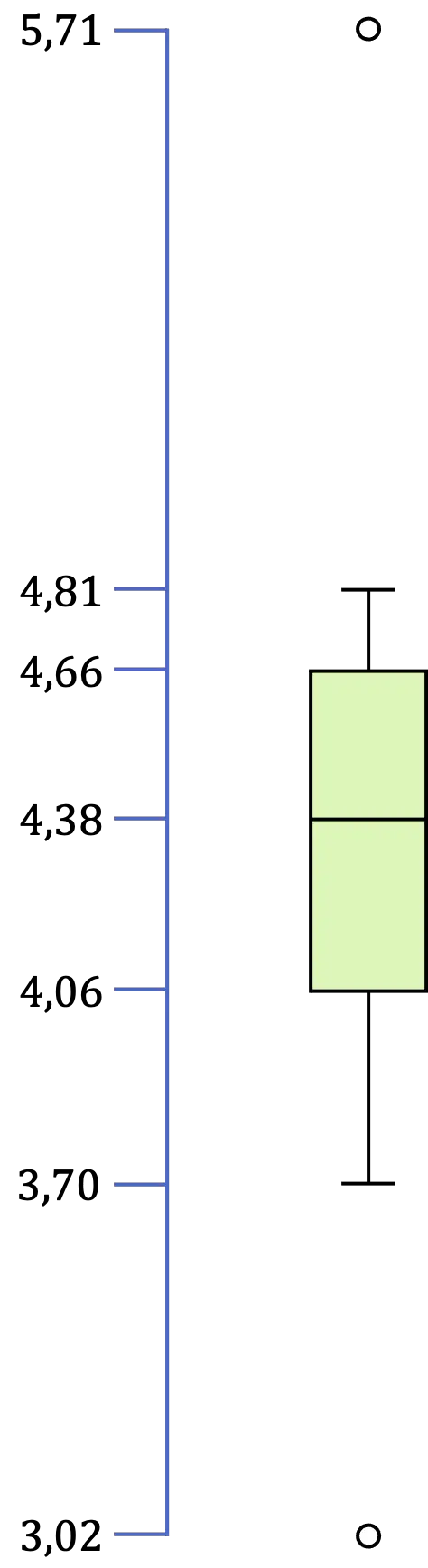
Donc, dans ce cas, nous avons deux valeurs aberrantes, car 3,02 est inférieur à 3,16 et 5,71 est supérieur à 5,56.

Enfin, il reste à identifier les valeurs extrêmes, qui sont le minimum et le maximum de toutes les données qui se trouvent dans l’intervalle [LI,LS]. Par conséquent, dans notre exemple, la valeur minimale est de 3,70 et la valeur maximale est de 4,81.

Ainsi, une fois que nous avons identifié toutes les valeurs du box et du whisker plot, il ne reste plus qu’à faire la représentation graphique :

À quoi sert un diagramme en boîte et moustaches ?

Enfin, voyons à quoi cela sert et comment interpréter le box and whisker plot (ou boxplot).

Évidemment, le diagramme en boîte et moustaches est très utile pour connaître rapidement les quartiles, l’intervalle interquartile, la médiane, les valeurs extrêmes et les valeurs aberrantes d’une série de données, puisque toutes ces mesures statistiques peuvent être identifiées avec un simple voir.

De plus, le diagramme en boîte et moustaches est utilisé pour analyser la symétrie de l’échantillon statistique, car il représente visuellement l’ensemble des données. Si la médiane n’est pas au centre de la boîte, cela signifie que l’échantillon n’est pas symétrique.

De même, les boxplots sont largement utilisés en bourse pour représenter la variation du prix d’une action sur une période de temps, car ils permettent de voir la valeur maximale, la valeur minimale et les valeurs intermédiairesdans un court laps de temps. temps et ainsi prendre des décisions plus rapides.