Comment effectuer une transformation Box-Cox en Python

Une transformation box-cox est une méthode couramment utilisée pour transformer un ensemble de données non normalement distribué en un ensemble plusnormalement distribué .

L’idée de base derrière cette méthode est de trouver une valeur pour λ telle que les données transformées soient aussi proches que possible de la distribution normale, en utilisant la formule suivante :

• y(λ) = (y ^λ – 1) / λ si y ≠ 0
• y(λ) = log(y) si y = 0

Nous pouvons effectuer une transformation box-cox en Python en utilisant la fonction scipy.stats.boxcox() .

L’exemple suivant montre comment utiliser cette fonction dans la pratique.

Exemple : transformation Box-Cox en Python

Supposons que nous générions un ensemble aléatoire de 1 000 valeurs provenant d’une distribution exponentielle :

#load necessary packages
import numpy as np 
from scipy.stats import boxcox 
import seaborn as sns 

#make this example reproducible
np.random.seed(0)

#generate dataset
data = np.random.exponential(size=1000)

#plot the distribution of data values
sns.distplot(data, hist=False, kde=True) 

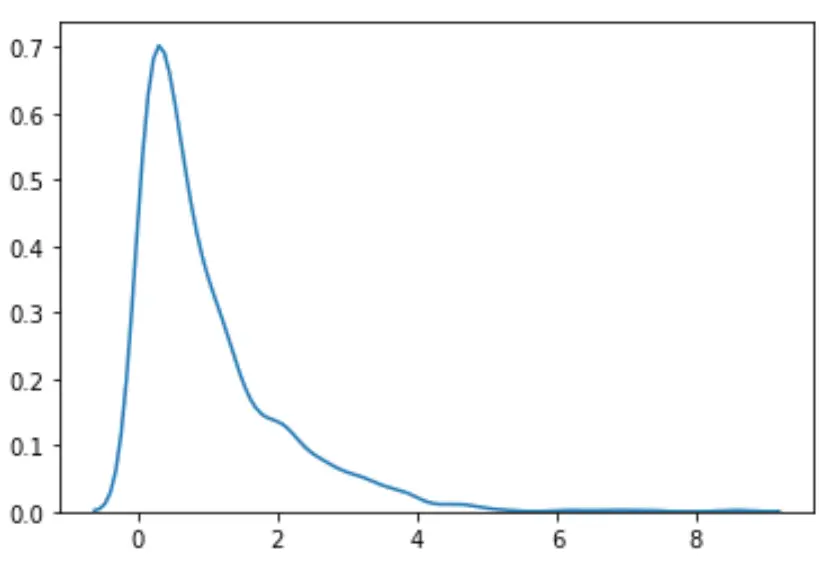
Nous pouvons constater que la distribution ne semble pas normale.

Nous pouvons utiliser la fonction boxcox() pour trouver une valeur optimale de lambda qui produit une distribution plus normale :

#perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns.distplot(transformed_data, hist=False, kde=True) 

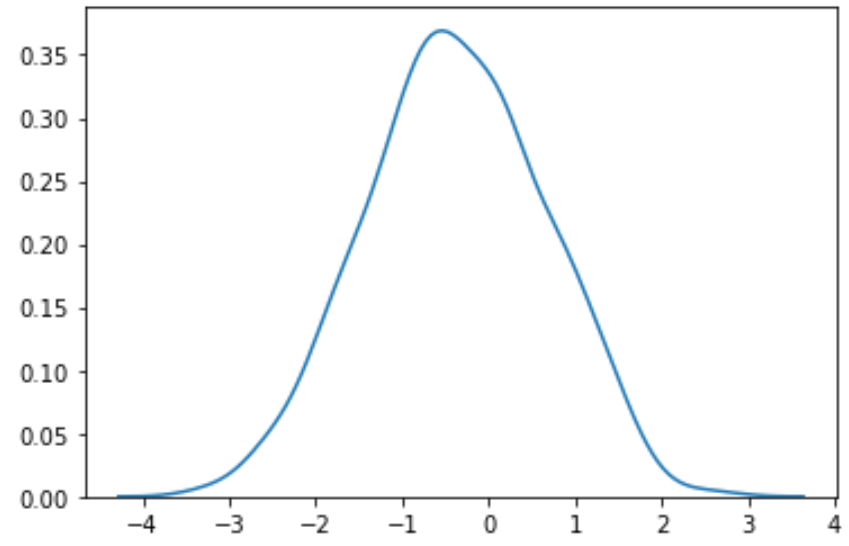
Nous pouvons voir que les données transformées suivent une distribution beaucoup plus normale.

On peut également retrouver la valeur lambda exacte utilisée pour effectuer la transformation Box-Cox :

#display optimal lambda value
print(best_lambda)

0.2420131978174143

Le lambda optimal s’est avéré être d’environ 0,242 .

Ainsi, chaque valeur de données a été transformée à l’aide de l’équation suivante :

Nouveau = (ancien ^0,242 – 1) / 0,242

Nous pouvons le confirmer en examinant les valeurs des données originales par rapport aux données transformées :

#view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062,  0.23427768, -0.07911706, -0.23247555, -0.55495228])

La première valeur de l’ensemble de données d’origine était 0,79587 . Ainsi, nous avons appliqué la formule suivante pour transformer cette valeur :

Nouveau = (.79587 ^0,242 – 1) / 0,242 = -0,222

Nous pouvons confirmer que la première valeur de l’ensemble de données transformé est bien -0,222 .

Ressources additionnelles

Comment créer et interpréter un tracé QQ en Python
Comment effectuer un test de normalité Shapiro-Wilk en Python