Comment calculer la dissimilarité de Bray-Curtis dans R
La dissimilarité de Bray-Curtis est un moyen de mesurer la dissimilarité entre deux sites différents.
Il est souvent utilisé en écologie et en biologie pour quantifier la différence entre deux sites en termes d’espèces trouvées dans ces sites.
Il est calculé comme suit :
BC ij = 1 – (2*C ij ) / (S i + S j )
où:
- C ij : La somme des valeurs les plus faibles pour les espèces trouvées dans chaque site.
- S i : Le nombre total de spécimens comptés sur le site i
- S j : Le nombre total de spécimens comptés sur le site j
La dissimilarité de Bray-Curtis est toujours comprise entre 0 et 1 où :
- 0 indique que deux sites n’ont aucune dissimilarité. En d’autres termes, ils partagent exactement le même nombre de chaque type d’espèce.
- 1 indique que deux sites présentent une dissemblance totale. En d’autres termes, ils ne partagent aucune espèce du même type.
Par exemple, supposons qu’un botaniste sorte et compte le nombre de cinq espèces végétales différentes (A, B, C, D et E) dans deux sites différents.
Le tableau suivant résume les données qu’elle a collectées :
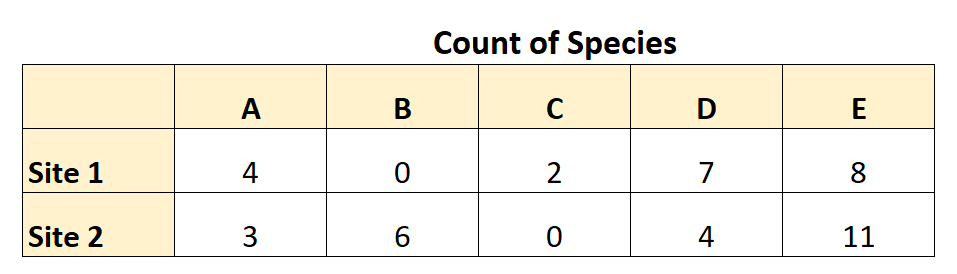
En utilisant ces données, elle peut calculer la dissimilarité de Bray-Curtis comme suit :
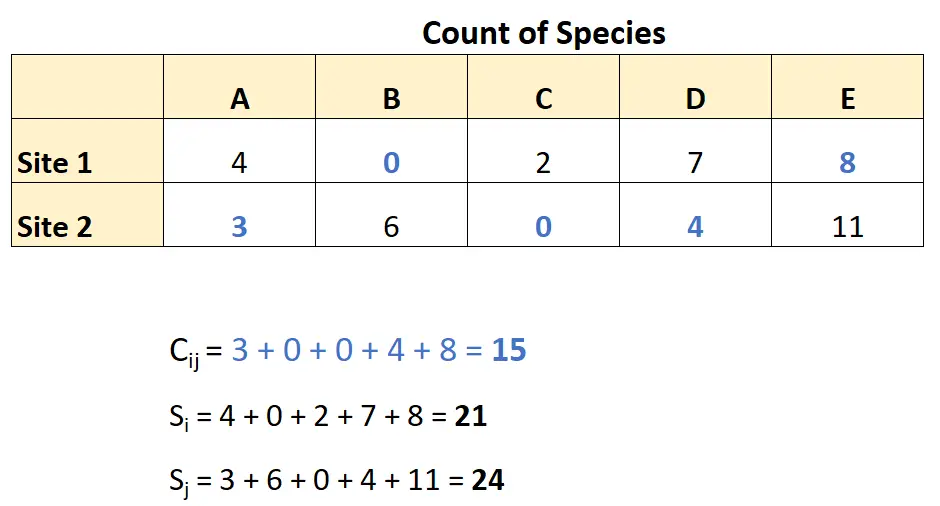
En intégrant ces nombres à la formule de dissimilarité de Bray-Curtis, nous obtenons :
- BC ij = 1 – (2*C ij ) / (S i + S j )
- BC ij = 1 – (2*15) / (21 + 24)
- BC ij = 0,33
La dissimilarité Bray-Curtis entre ces deux sites est de 0,33 .
L’exemple suivant montre comment calculer la dissimilarité de Bray-Curtis dans R.
Exemple : calcul de la dissimilarité de Bray-Curtis dans R
Tout d’abord, créons le bloc de données suivant dans R pour contenir nos valeurs de données :
#create data frame df <- data.frame(A=c(4, 3), B=c(0, 6), C=c(2, 0), D=c(7, 4), E=c(8, 11)) #view data frame df A B C D E 1 4 0 2 7 8 2 3 6 0 4 11
Nous pouvons utiliser le code suivant pour calculer la dissimilarité de Bray-Curtis entre les deux lignes du bloc de données :
#calculate Bray-Curtis dissimilarity sum(apply(df, 2, function(x) abs(max(x)-min(x)))) / sum(rowSums(df)) [1] 0.3333333
Le Bray-Curtis s’avère être de manière différente 0,33 .
Cela correspond à la valeur que nous avons calculée manuellement plus tôt.
Remarque : Cette formule ne fonctionnera que si chaque ligne du bloc de données représente un site distinct.
Ressources additionnelles
Les didacticiels suivants expliquent comment calculer d’autres métriques de similarité dans R :
Comment calculer la similarité Jaccard dans R
Comment calculer la similarité cosinus dans R
